Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2025-01-03T18:37:20.040Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW SUM–PRODUCT ESTIMATE IN PRIME FIELDS

Part of: Finite fields and commutative rings (number-theoretic aspects) Designs and configurations

Published online by Cambridge University Press:  24 May 2019

CHANGHAO CHEN ,
BRYCE KERR  and
ALI MOHAMMADI
CHANGHAO CHEN
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney, NSW 2052, Australia email [email protected]
BRYCE KERR*
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney, NSW 2052, Australia email [email protected]
ALI MOHAMMADI
Affiliation:
School of Mathematics and Statistics, University of Sydney, NSW 2006, Australia email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain a new sum–product estimate in prime fields for sets of large cardinality. In particular, we show that if 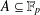$A\subseteq \mathbb{F}_{p}$ satisfies 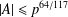$|A|\leq p^{64/117}$ then 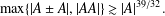$\max \{|A\pm A|,|AA|\}\gtrsim |A|^{39/32}.$ Our argument builds on and improves some recent results of Shakan and Shkredov [‘Breaking the 6/5 threshold for sums and products modulo a prime’, Preprint, 2018, arXiv:1806.07091v1] which use the eigenvalue method to reduce to estimating a fourth moment energy and the additive energy 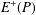$E^{+}(P)$ of some subset 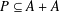$P\subseteq A+A$. Our main novelty comes from reducing the estimation of 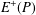$E^{+}(P)$ to a point–plane incidence bound of Rudnev [‘On the number of incidences between points and planes in three dimensions’, Combinatorica 38(1) (2017), 219–254] rather than a point–line incidence bound used by Shakan and Shkredov.

Keywords

sum–product estimateadditive combinatorics

MSC classification

Primary: 11T99: None of the above, but in this section
Secondary: 05B10: Difference sets (number-theoretic, group-theoretic, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 268 - 280
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first and second author were supported by ARC Grant DP170100786.

References

Bourgain, J. and Garaev, M. Z., ‘On a variant of sum-product estimates and explicit exponential sum bounds in prime fields’, Math. Proc. Cambridge Philos. Soc. 146(1) (2009), 1–21.Google Scholar
Bourgain, J., Katz, N. and Tao, T., ‘A sum-product estimate in finite fields and their applications’, Geom. Funct. Anal. 14 (2004), 27–57.Google Scholar
Elekes, G., ‘On the number of sums and products’, Acta Arith. 81 (1997), 365–367.Google Scholar
Erdős, P. and Szemerédi, E., ‘On sums and products of integers’, in: Studies in Pure Mathematics. To the memory of Paul Turán (Birkhäuser, Basel, 1983), 213–218.Google Scholar
Garaev, M. Z., ‘An explicit sum-product estimate in 𝔽p ’, Int. Math. Res. Not. IMRN 2007 (2007), Article ID 11, 11 pages.Google Scholar
Garaev, M. Z., ‘The sum-product estimate for large subsets of prime fields’, Proc. Amer. Math. Soc. 136 (2008), 2735–2739.Google Scholar
Glibichuk, A. A. and Konyagin, S. V., ‘Additive properties of product sets in fields of prime order’, in: Additive Combinatorics, CRM Proceedings and Lecture Notes, 43 (American Mathematical Society, Providence, RI, 2007), 279–286.Google Scholar
Katz, N. H. and Shen, C. Y., ‘A slight improvement to Garaev’s sum product estimate’, Proc. Amer. Math. Soc. 136 (2008), 2499–2504.Google Scholar
Konyagin, S. V. and Rudnev, M., ‘On new sum-product type estimates’, SIAM J. Discrete Math. 27(2) (2013), 973–990.Google Scholar
Li, L., ‘Slightly improved sum-product estimates in fields of prime order’, Acta Arith. 147 (2011), 153–160.Google Scholar
Murphy, B., Roche-Newton, O. and Shkredov, I., ‘Variations of the sum-product problem’, SIAM J. Discrete Math. 29(1) (2015), 514–540.Google Scholar
Murphy, B., Petridis, G., Roche-Newton, O., Rudnev, M. and Shkredov, I. D., ‘New results on sum-product type growth over fields’, Preprint, 2017, arXiv:1702.01003.Google Scholar
Murphy, B., Rudnev, M., Shkredov, I. and Shteinikov, Y., ‘On the few products, many sums problem’, Preprint, 2017, arXiv:1712.0041v1.Google Scholar
Roche-Newton, O., Rudnev, M. and Shkredov, I. D., ‘New sum-product type estimates over finite fields’, Adv. Math. 293 (2016), 589–605.Google Scholar
Rudnev, M., ‘An improved sum-product inequality in fields of prime order’, Int. Math. Res. Not. IMRN 2012(16) (2012), 3693–3705.Google Scholar
Rudnev, M., ‘On the number of incidences between points and planes in three dimensions’, Combinatorica 38(1) (2017), 219–254.Google Scholar
Rudnev, M., Shakan, G. and Shkredov, I., ‘Stronger sum-product inequalities for small sets’, Preprint, 2018, arXiv:1808.08465.Google Scholar
Shakan, G., ‘On higher energy decomposition and the sum-product phenomenon’, Math. Proc. Came. Phil. Soc., to appear.Google Scholar
Shakan, G. and Shkredov, I. D., ‘Breaking the 6/5 threshold for sums and products modulo a prime’, Preprint, 2018, arXiv:1806.07091v1.Google Scholar
Shkredov, I. D., ‘Energies and structure of additive sets’, Electron. J. Combin. 21(3) (2014), 1–53.Google Scholar
Shkredov, I. D., ‘On asymptotic formulae in some sum-product questions’, Preprint, 2018, arXiv:1802.09066.Google Scholar
Stevens, S. and de Zeeuw, F., ‘An improved point-line incidence bound over arbitrary fields’, Bull. Lond. Math. Soc. 49(5) (2017), 842–858.Google Scholar