No CrossRef data available.
Published online by Cambridge University Press: 17 April 2009
Let {zj} be an interpolation sequence in the open unit disc and {wj} a bounded sequence. In this note, it is shown that there is a function F in H∞ + C satisfying ‖F‖ ≤ 1 and 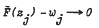 as j → ∞ if and only if there exists a compact matrix [tij] such that
as j → ∞ if and only if there exists a compact matrix [tij] such that 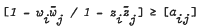 on
on 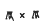 where
where 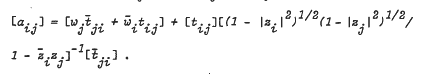 .
.