Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T23:23:09.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Multipliers on weighted function spaces over locally compact vilenkin groups

Published online by Cambridge University Press:  17 April 2009

Yueping Zhu
Yueping Zhu
Affiliation:
Department of Mathematics, Nantong Teachers' College, Nantong, 226007, jiangsu Province, People's Republic of China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, we consider multipliers on weighted function spaces over totally disconnected locally compact Abelian groups (Vilenkin groups). First we present an 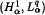multiplier result. Then we give an 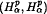multiplier result under a similar condition of Lu-Yang type. In Section 3, we obtain a result about the boundedness of multipliers on weighted Besov spaces.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 65 , Issue 2 , April 2002 , pp. 337 - 351
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Edwards, R.E. and Gaudry, G.I., Littlewood-Paley and multiplier theory (Springer-Verlag, Berlin, 1977).CrossRefGoogle Scholar
[2]Frazier, M. and Jawerth, B., ‘Decomposition of Besov spaces’, Indiana Univ. Math. J. 34 (1985), 777–799.CrossRefGoogle Scholar
[3]Gaudry, G.I. and Inglis, I.R., ‘Approximation of multipliers’, Proc. Amer. Math. Soc. 44 (1974), 381–384.Google Scholar
[4]Gaudry, G.I. and Inglis, I.R., ‘Weak-strong convolution operators on certain disconnected groups’, Studia Math. 64 (1979), 1–12.CrossRefGoogle Scholar
[5]Kitada, T., ‘H p multiplier theorems on certain totally disconnected groups’, Internat. J. Math. Sci. 11 (1988), 665–674.CrossRefGoogle Scholar
[6]Kitada, T., ‘Weighted Triebel-Lizorkin spaces on locally compact Vilenkin groups’, Math. Nachr. 168 (1994), 191–208.CrossRefGoogle Scholar
[7]Lu, S.Z. and yang, D.C., ‘Weak Hardy spaces over locally compact Vilenkin groups’, J. Beijing Normal Univ. (Natur. Sci.) 28 (1992), 409–419.Google Scholar
[8]Ombe, H., ‘Besov spaces and Bessel potential spaces on certain groups’, Proc. Japan Acad. Ser. A Math. Sci. 67 (1991), 6–10.Google Scholar
[9]Onneweer, C.W. and Quek, T.S., ‘Littlewood-Paley and multiplier theorems on weighted spaces over locally compact Vilenkin groups’, J. Math Anal. Appl. 210 (1997), 742–754.Google Scholar
[10]Onneweer, C.W. and Quek, T.S., ‘L p multipliers of mixed-norm on locally compact Vilenkin groups’, J. Austral. Math. Soc. Ser. A 645 (1999), 370–387.Google Scholar
[11]Onneweer, C.W. and Quek, T.S., ‘Multipliers on weighted Hardy spaces over locally compact Vilenkin groups’, J. Austral. Math. Soc. Ser. A 48 (1990), 472–496.CrossRefGoogle Scholar
[12]Onneweer, C.W. and Quek, T.S., ‘Multipliers on weighted Hardy spaces over locally compact Vilenkin groups II’, Colloq. Math. 60/61 (1990), 305–314.Google Scholar
[13]Onneweer, C.W. and Su, W., ‘Homogeneous Besov spaces on locally compact Vilenkin groups’, Studia Math. 93 (1989), 17–39.CrossRefGoogle Scholar
[14]Saloff-Coste, L., ‘Opéateurs pseudo-differentiels sur certains groupes totalement discontinus’, Studia Math. 83 (1986), 205–228.Google Scholar
[15]Taibleson, M.H., Fourier analysis on local fields (Princeton Univrsity Press, princeton, N.J., 1975).Google Scholar
[16]Triebel, H., Theory of function spaces (Birkhäuser, Basel, 1983).CrossRefGoogle Scholar
[17]Vilenkin, N.Ja., ‘On a class of complete orthonormal systems’, Amer. Math. Soc. Transl. Ser. 228 (1963), 1–35.Google Scholar
[18]Zhu, Y., ‘Multipliers on weighted Hardy spaces over locally compact Vilenkin groups’, Chinese Quart. J. Math. 15 (2000), 18–26.Google Scholar