Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T15:24:50.835Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MULTIPLIER ALGEBRA OF A BEURLING ALGEBRA

Part of: Commutative Banach algebras and commutative topological algebras Semigroups

Published online by Cambridge University Press:  15 May 2014

S. J. BHATT ,
P. A. DABHI  and
H. V. DEDANIA
S. J. BHATT
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar 388120, Gujarat, India email [email protected]
P. A. DABHI*
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar 388120, Gujarat, India email [email protected]
H. V. DEDANIA
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar 388120, Gujarat, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a discrete abelian cancellative semigroup 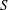$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}S$ with a weight function 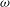$\omega $ and associated multiplier semigroup 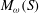$M_\omega (S)$ consisting of 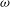$\omega $-bounded multipliers, the multiplier algebra of the Beurling algebra of 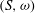$(S,\omega )$ coincides with the Beurling algebra of 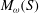$M_\omega (S)$ with the induced weight.

Keywords

Banach algebraBeurling algebramultiplier algebra

MSC classification

Secondary: 46J05: General theory of commutative topological algebras 20M15: Mappings of semigroups 20M14: Commutative semigroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 1 , August 2014 , pp. 113 - 120
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bhatt, S. J., Dabhi, P. A. and Dedania, H. V., ‘Beurling algebra analogues of theorems of Wiener–Lévy–Żelazko and Żelazko’, Stud. Math. 195 (2009), 219–225.CrossRefGoogle Scholar
Bhatt, S. J., Dabhi, P. A. and Dedania, H. V., ‘Multipliers of weighted semigroups and associated Beurling Banach algebras’, Proc. Indian Acad. Sci. Math. Sci. 121 (2011), 417–433.CrossRefGoogle Scholar
Bhatt, S. J. and Dedania, H. V., ‘Beurling algebra analogues of the classical theorems of Wiener and Lévy on absolutely convergent Fourier series’, Proc. Indian Acad. Sci. Math. Sci. 113 (2003), 179–182.Google Scholar
Dales, H. G., Banach Algebras and Automatic Continuity, London Mathematical Society Monographs Series, 24 (Clarendon Press, Oxford, 2000).Google Scholar
Dales, H. G. and Dedania, H. V., ‘Weighted convolution algebras on subsemigroups of the real line’, Dissertationes Math. (Rozprawy Mat.) 459 (2009), 1–60.Google Scholar
Edwards, R. E., Fourier Series, Vol. II (Holt, Rinehart and Winston, New York, 1967).Google Scholar
Gel’fand, I. M., Raǐkov, D. and Šilov, G. E., Commutative Normed Rings (Chelsea Publishing Company, New York, 1964).Google Scholar
Hewitt, E. and Zuckerman, H. S., ‘The ℓ 1algebra of a commutative semigroup’, Trans. Amer. Math. Soc. 83 (1956), 70–97.Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory (Clarendon Press, Oxford, 1995).Google Scholar
Kaniuth, E., A Course in Commutative Banach Algebras (Springer, New York, 2009).Google Scholar
Lahr, C. D., ‘Multipliers for ℓ 1-algebras with approximate identities’, Proc. Amer. Math. Soc. 42 (1974), 501–506.Google Scholar
Lahr, C. D., ‘Multipliers of certain convolution measure algebras’, Trans. Amer. Math. Soc. 185 (1976), 165–181.CrossRefGoogle Scholar
Larsen, R., An Introduction to the Theory of Multipliers (Springer, Berlin, 1971).Google Scholar
Reiter, H. and Stegeman, J. D., Classical Harmonic Analysis and Locally Compact Abelian Groups (Clarendon Press, Oxford, 2000).Google Scholar