Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Reukers, F.
1981.
Padé Approximation and its Applications Amsterdam 1980.
Vol. 888,
Issue. ,
p.
90.
Rhin, Georges
and
Toffin, Philippe
1986.
Approximants de Padé simultanés de logarithmes.
Journal of Number Theory,
Vol. 24,
Issue. 3,
p.
284.
Rivoal, Tanguy
2012.
On the arithmetic nature of the values of the gamma function, Euler's constant, and Gompertz's constant.
Michigan Mathematical Journal,
Vol. 61,
Issue. 2,
Qin, Hai-Hua
and
Liu, Xiaodong
2015.
The interior inverse scattering problem for cavities with an artificial obstacle.
Applied Numerical Mathematics,
Vol. 88,
Issue. ,
p.
18.
2021.
An Introduction to Hypergeometric, Supertrigonometric, and Superhyperbolic Functions.
p.
471.
Karatsuba, E. A.
2021.
On an Evaluation Method for Zeta Constants Based on a Number Theoretic Approach.
Problems of Information Transmission,
Vol. 57,
Issue. 3,
p.
265.
Yang, Xiao-Jun
2021.
An Introduction to Hypergeometric, Supertrigonometric, and Superhyperbolic Functions.
p.
345.
KAWASHIMA, MAKOTO
2024.
RODRIGUES FORMULA AND LINEAR INDEPENDENCE FOR VALUES OF HYPERGEOMETRIC FUNCTIONS WITH VARYING PARAMETERS.
Journal of the Australian Mathematical Society,
Vol. 117,
Issue. 3,
p.
308.


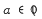 , π
, π