Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T06:45:13.076Z Has data issue: false hasContentIssue false
  • English
  • Français

LEE MONOIDS ARE NONFINITELY BASED WHILE THE SETS OF THEIR ISOTERMS ARE FINITELY BASED

Part of: Semigroups Varieties

Published online by Cambridge University Press:  28 March 2018

OLGA SAPIR Open the ORCID record for OLGA SAPIR [Opens in a new window]
OLGA SAPIR*
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN 37240, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We establish a new sufficient condition under which a monoid is nonfinitely based and apply this condition to Lee monoids 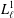$L_{\ell }^{1}$, obtained by adjoining an identity element to the semigroup generated by two idempotents $a$ and 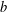$b$ with the relation 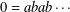$0=abab\cdots \,$ (length 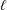$\ell$). We show that every monoid 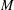$M$ which generates a variety containing 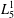$L_{5}^{1}$ and is contained in the variety generated by 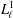$L_{\ell }^{1}$ for some 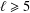$\ell \geq 5$ is nonfinitely based. We establish this result by analysing $\unicode[STIX]{x1D70F}$-terms for 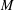$M$, where $\unicode[STIX]{x1D70F}$ is a certain nontrivial congruence on the free semigroup. We also show that if $\unicode[STIX]{x1D70F}$ is the trivial congruence on the free semigroup and 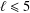$\ell \leq 5$, then the $\unicode[STIX]{x1D70F}$-terms (isoterms) for 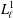$L_{\ell }^{1}$ carry no information about the nonfinite basis property of 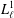$L_{\ell }^{1}$.

Keywords

Lee monoidsidentityfinite basis problemnonfinitely basedvarietyisoterm

MSC classification

Primary: 20M07: Varieties and pseudovarieties of semigroups
Secondary: 08B05: Equational logic, Mal′cev (Mal′tsev) conditions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 422 - 434
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Edmunds, C. C., ‘On certain finitely based varieties of semigroups’, Semigroup Forum 15(1) (1977), 21–39.CrossRefGoogle Scholar
Edmunds, C. C., ‘Varieties generated by semigroups of order four’, Semigroup Forum 21(1) (1980), 67–81.Google Scholar
Jackson, M. G., ‘Finiteness properties of varieties and the restriction to finite algebras’, Semigroup Forum 70 (2005), 159–187.CrossRefGoogle Scholar
Jackson, M. G. and Sapir, O. B., ‘Finitely based, finite sets of words’, Internat. J. Algebra Comput. 10(6) (2000), 683–708.Google Scholar
Lee, E. W. H., ‘A sufficient condition for the non-finite basis property of semigroups’, Monatsh. Math. 168 (2012), 461–472.Google Scholar
Lee, E. W. H., ‘On a class of completely join prime J-trivial semigroups with unique involution’, Algebra Universalis 78 (2017), 131–145.Google Scholar
Lee, E. W. H., ‘A sufficient condition for the absence of irredundant bases’, Houston J. Math. (to appear).Google Scholar
Mikhaylova, I. A. and Sapir, O. B., ‘Lee monoid $L_{4}^{1}$ is nonfinitely based’, Preprint, 2017, arXiv:1710.00820 [math.GR].Google Scholar
Perkins, P., ‘Bases for equational theories of semigroups’, J. Algebra 11 (1969), 298–314.CrossRefGoogle Scholar
Sapir, M. V., ‘Problems of Burnside type and the finite basis property in varieties of semigroups’, Izv. Akad. Nauk SSSR Ser. Mat. 51 (1987), 319–340 (in Russian); English translation Math. USSR Izv. 30(2) (1988), 295–314.Google Scholar
Sapir, O. B., ‘Nonfinitely based monoids’, Semigroup Forum 90(3) (2015), 557–586.CrossRefGoogle Scholar
Sapir, O. B., ‘The finite basis problem for words with at most two non-linear variables’, Semigroup Forum 93(1) (2016), 131–151.Google Scholar
Volkov, M. V., ‘The finite basis problem for finite semigroups’, Sci. Math. Jpn. 53 (2001), 171–199.Google Scholar
Zhang, W. T., ‘Existence of a new limit variety of aperiodic monoids’, Semigroup Forum 86 (2013), 212–220.Google Scholar
Zhang, W. T. and Luo, Y. F., ‘A new example of nonfinitely based semigroups’, Bull. Aust. Math. Soc. 84 (2011), 484–491.Google Scholar