Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2025-01-03T19:12:54.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinitary harmonic numbers

Published online by Cambridge University Press:  17 April 2009

Peter Hagis Jr  and
Graeme L. Cohen
Peter Hagis Jr
Affiliation:
Department of Mathematics, Temple University, Philadelphia PA 19122, United States of America
Graeme L. Cohen
Affiliation:
School of Mathematical Sciences, University of Technology, Sydney, Broadway NSW 2007, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The infinitary divisors of a natural number n are the products of its divisors of the 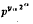, where py is an exact prime-power divisor of n and 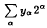(where yα = 0 or 1) is the binary representation of y. Infinitary harmonic numbers are those for which the infinitary divisors have integer harmonic mean. One of the results in this paper is that the number of infinitary harmonic numbers not exceeding x is less than 2.2 x1/2 2(1+ε)log x/log log x for any ε > 0 and x > n0(ε). A corollary is that the set of infinitary perfect numbers (numbers n whose proper infinitary divisors sum to n) has density zero.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 41 , Issue 1 , February 1990 , pp. 151 - 158
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Cohen, G.L., ‘On an integer's infinitary divisors’, Math. Comp. (to appear).Google Scholar
[2]Golomb, S.W., ‘Powerful numbers’, Amer. Math. Monthly 77 (1970), 848–855.CrossRefGoogle Scholar
[3]Hagis, P. Jr and Lord, G., ‘Unitary harmonic numbers’, Proc. Amer. Math. Soc. 51 (1975), 1–7.CrossRefGoogle Scholar
[4]Hardy, G.H. and Wright, E. M., An Introduction to the Theory of Numbers, (4th ed.) (Oxford University Press, London, 1960).Google Scholar
[5]Ore, O., ‘On the averages of the divisors of a number’, Amer. Math. Monthly 55 (1948), 615–619.CrossRefGoogle Scholar