Let G be a finite group and F a complete local noetherian commutative ring with residue field 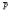of characteristic p # 0. Let A(G) denote the representation algebra of G with respect to F. This is a linear algebra over the complex field whose basis elements are the isomorphism-classes of indecomposable finitely generated FG-representation modules, with addition and multiplication induced by direct sum and tensor product respectively. The two authors have separately found decompositions of A(G) as direct sums of subalgebras. In this note we show that the decompositions in one case have a common refinement given in the other's paper.