Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T04:15:19.121Z Has data issue: false hasContentIssue false
  • English
  • Français

HEREDITARY TORSION THEORIES OF A LOCALLY NOETHERIAN GROTHENDIECK CATEGORY

Part of: Abelian categories

Published online by Cambridge University Press:  26 September 2016

KAIVAN AHMADI  and
REZA SAZEEDEH
KAIVAN AHMADI
Affiliation:
Department of Mathematics, Urmia University, PO Box 165, Urmia, Iran email [email protected]
REZA SAZEEDEH*
Affiliation:
Department of Mathematics, Urmia University, PO Box 165, Urmia, Iran email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 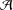${\mathcal{A}}$ be a locally noetherian Grothendieck category. We construct closure operators on the lattice of subcategories of ${\mathcal{A}}$ and the lattice of subsets of 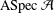$\text{ASpec}\,{\mathcal{A}}$ in terms of associated atoms. This establishes a one-to-one correspondence between hereditary torsion theories of 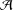${\mathcal{A}}$ and closed subsets of 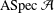$\text{ASpec}\,{\mathcal{A}}$ . If 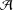${\mathcal{A}}$ is locally stable, then the hereditary torsion theories can be studied locally. In this case, we show that the topological space 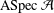$\text{ASpec}\,{\mathcal{A}}$ is Alexandroff.

Keywords

atom spectrumGrothendieck categorylocalising subcategory

MSC classification

Primary: 18E15: Grothendieck categories
Secondary: 18E40: Torsion theories, radicals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 421 - 430
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Gabriel, P., ‘Des catégories abéliennes’, Bull. Soc. Math. France 90 (1962), 323–448.CrossRefGoogle Scholar
Herzog, I., ‘The Ziegler spectrum of a locally coherent Grothendieck category’, Proc. Lond. Math. Soc. (3) 73(3) (1997), 503–558.Google Scholar
Hovey, M., ‘Classifying subcategories of modules’, Trans. Amer. Math. Soc. 353 (2001), 3181–3191.Google Scholar
Kanda, R., ‘Classifying Serre subcategories via atom spectrum’, Adv. Math. 231(3–4) (2012), 1572–1588.Google Scholar
Kanda, R., ‘Classification of categorical subspaces of locally noetherian schemes’, Doc. Math. 20 (2015), 1403–1465.Google Scholar
Krause, H., ‘The spectrum of a locally coherent category’, J. Pure Appl. Algebra 114(3) (1991), 259–271.Google Scholar
Popoescu, N., Abelian Categories with Applications to Rings and Modules, London Mathematical Society Monographs, 3 (Academic Press, London–New York, 1973).Google Scholar
Sazeedeh, R., ‘Monoform objects and localization theory in abelian categories’, submitted.Google Scholar
Stenstrom, B., Rings of Quotients: An Introduction to Methods of Ring Theory (Springer, Berlin, 1975).Google Scholar
Takahashi, R., ‘Classifying subcategories of modules over a commutative noetherian ring’, J. Lond. Math. Soc. (2) 78(3) (2008), 767–782.Google Scholar
Thomason, R. W., ‘The classification of triangulated subcategories’, Compositio Math. 105 (1997), 11–27.Google Scholar