Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Deville, Robert
and
Ghoussoub, Nassif
2001.
Vol. 1,
Issue. ,
p.
393.
Gaumont, D.
Kamburova, D.
and
Revalski, J. P.
2019.
Perturbations of Supinf Problems with Constraints.
Vietnam Journal of Mathematics,
Vol. 47,
Issue. 3,
p.
659.
Kamburova, Detelina
Marinov, Rumen
and
Zlateva, Nadia
2025.
Saddle Points in Completely Regular Topological Spaces.
Vietnam Journal of Mathematics,
Vol. 53,
Issue. 2,
p.
441.


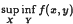 and give conditions under which the majority (in Baire category sense) of bounded functions
and give conditions under which the majority (in Baire category sense) of bounded functions 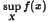 is well posed for the majority of bounded lsc real valued functions
is well posed for the majority of bounded lsc real valued functions 