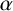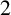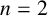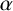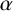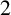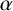1 Introduction
Throughout this paper, G will denote a finite group. Also, all the representations considered will be taken to be over the field of complex numbers. The set of all ordinary irreducible characters of G is denoted as usual by
![]() $\operatorname {\mathrm {Irr}}(G)$
, and
$\operatorname {\mathrm {Irr}}(G)$
, and
![]() $\operatorname {\mathrm {Lin}}(G)$
will denote the group of linear characters of
$\operatorname {\mathrm {Lin}}(G)$
will denote the group of linear characters of
![]() $G.$
$G.$
There are a number of results concerning
![]() $\operatorname {\mathrm {Irr}}(G)$
and Frobenius–Schur indicators, three of which are reviewed here. For the first, see [Reference Isaacs3, pages 49–50].
$\operatorname {\mathrm {Irr}}(G)$
and Frobenius–Schur indicators, three of which are reviewed here. For the first, see [Reference Isaacs3, pages 49–50].
Theorem 1.1. Define
![]() $\theta _n: G\rightarrow \mathbb {Z}_{\geq 0}$
by
$\theta _n: G\rightarrow \mathbb {Z}_{\geq 0}$
by
![]() $\theta _n(x) = \vert \{g\in G: g^n = x\}\vert $
for
$\theta _n(x) = \vert \{g\in G: g^n = x\}\vert $
for
![]() $n\in \mathbb {N}.$
Then
$n\in \mathbb {N}.$
Then
 $$ \begin{align*}\theta_n = \sum_{\chi\in\operatorname{\mathrm{Irr}}(G)}v_n(\chi)\chi,\end{align*} $$
$$ \begin{align*}\theta_n = \sum_{\chi\in\operatorname{\mathrm{Irr}}(G)}v_n(\chi)\chi,\end{align*} $$
where
 $$ \begin{align*}v_n(\chi) = \frac{1}{\vert G\vert}\sum_{x\in G}\chi(x^n)\end{align*} $$
$$ \begin{align*}v_n(\chi) = \frac{1}{\vert G\vert}\sum_{x\in G}\chi(x^n)\end{align*} $$
is the nth Frobenius–Schur indicator of
![]() $\chi $
and
$\chi $
and
![]() $v_n(\chi )\in \mathbb {Z}.$
$v_n(\chi )\in \mathbb {Z}.$
The second result is a consequence of this theorem (see [Reference Isaacs3, Corollary 4.6]).
Corollary 1.2. Let G have exactly t involutions. Then
 $$ \begin{align*}1+t =\sum_{\chi\in\operatorname{\mathrm{Irr}}(G)}v_2(\chi)\chi(1).\end{align*} $$
$$ \begin{align*}1+t =\sum_{\chi\in\operatorname{\mathrm{Irr}}(G)}v_2(\chi)\chi(1).\end{align*} $$
An element of G is real if it is conjugate to its inverse and
![]() $\chi \in \operatorname {\mathrm {Irr}}(G)$
is real if
$\chi \in \operatorname {\mathrm {Irr}}(G)$
is real if
![]() $\chi (x)\in \mathbb {R}$
for all
$\chi (x)\in \mathbb {R}$
for all
![]() $x\in G.$
For the third result connecting these two concepts, see [Reference Isaacs3, Problem 6.13].
$x\in G.$
For the third result connecting these two concepts, see [Reference Isaacs3, Problem 6.13].
Theorem 1.3. The number of real conjugacy classes of G is equal to the number of real
![]() $\chi \in \operatorname {\mathrm {Irr}}(G).$
$\chi \in \operatorname {\mathrm {Irr}}(G).$
The purpose of this paper is to find generalisations of these three results if irreducible projective characters of G are considered instead of ordinary ones. To generalise Theorem 1.1 it will be necessary to define the nth Frobenius–Schur indicator of an irreducible projective character of
![]() $G.$
A number of remarks and examples were made and given in [Reference Humphreys2, pages 27–28] to show that this and Theorem 1.3 do not have a straightforward generalisation to the projective character situation, but our approach overcomes those difficulties.
$G.$
A number of remarks and examples were made and given in [Reference Humphreys2, pages 27–28] to show that this and Theorem 1.3 do not have a straightforward generalisation to the projective character situation, but our approach overcomes those difficulties.
In Section 2, basic facts about projective representations of G with
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
will be stated. The nth Frobenius–Schur indicator of an irreducible projective character of G is then defined and interpreted for
$\alpha $
will be stated. The nth Frobenius–Schur indicator of an irreducible projective character of G is then defined and interpreted for
![]() $n = 2.$
Using this, the generalisations sought of the three results will be found in Section 3, although for the last two restricted to the case when both
$n = 2.$
Using this, the generalisations sought of the three results will be found in Section 3, although for the last two restricted to the case when both
![]() $\alpha $
and its cohomology class have order
$\alpha $
and its cohomology class have order
![]() $2$
.
$2$
.
2 Frobenius–Schur indicators for projective characters
All of the standard facts and concepts relating to projective representations below may be found in [Reference Karpilovsky4, Reference Karpilovsky5], or (albeit to a lesser extent) [Reference Isaacs3, Ch. 11] or [Reference Haggarty and Humphreys1].
Definition 2.1. A
![]() $2$
-cocycle of G over
$2$
-cocycle of G over
![]() $\mathbb {C}$
is a function
$\mathbb {C}$
is a function
![]() $\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
$\alpha : G\times G\rightarrow \mathbb {C}^*$
such that
![]() $\alpha (1, 1) = 1$
and
$\alpha (1, 1) = 1$
and
![]() $\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
$\alpha (x, y)\alpha (xy, z) = \alpha (x, yz)\alpha (y, z)$
for all x, y,
![]() $z\in G.$
$z\in G.$
The set of all such
![]() $2$
-cocycles of G form a group
$2$
-cocycles of G form a group
![]() $Z^2(G, \mathbb {C}^*)$
under multiplication. Let
$Z^2(G, \mathbb {C}^*)$
under multiplication. Let
![]() $\delta : G\rightarrow \mathbb {C}^*$
be any function with
$\delta : G\rightarrow \mathbb {C}^*$
be any function with
![]() $\delta (1) = 1.$
Then
$\delta (1) = 1.$
Then
![]() $t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
$t(\delta )(x, y) = \delta (x)\delta (y)/\delta (xy)$
for all
![]() $x, y\in G$
is a
$x, y\in G$
is a
![]() $2$
-cocycle of G, which is called a coboundary. Two
$2$
-cocycle of G, which is called a coboundary. Two
![]() $2$
-cocycles
$2$
-cocycles
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are cohomologous if there exists a coboundary
$\beta $
are cohomologous if there exists a coboundary
![]() $t(\delta )$
such that
$t(\delta )$
such that
![]() $\beta = t(\delta )\alpha .$
This defines an equivalence relation on
$\beta = t(\delta )\alpha .$
This defines an equivalence relation on
![]() $Z^2(G, \mathbb {C}^*)$
, and the cohomology classes
$Z^2(G, \mathbb {C}^*)$
, and the cohomology classes
![]() $[\alpha ]$
form a finite abelian group, called the Schur multiplier
$[\alpha ]$
form a finite abelian group, called the Schur multiplier
![]() $M(G).$
$M(G).$
Definition 2.2. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $G.$
Then
$G.$
Then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if
$\alpha $
-regular if
![]() $\alpha (x, y) = \alpha (y, x)$
for all
$\alpha (x, y) = \alpha (y, x)$
for all
![]() $y\in C_G(x).$
$y\in C_G(x).$
Let
![]() $\beta \in [\alpha ]$
. Then
$\beta \in [\alpha ]$
. Then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if it is
$\alpha $
-regular if and only if it is
![]() $\beta $
-regular. If x is
$\beta $
-regular. If x is
![]() $\alpha $
-regular then so too are
$\alpha $
-regular then so too are
![]() $x^{-1}$
and any conjugate of
$x^{-1}$
and any conjugate of
![]() $x,$
so from the latter one may refer to the
$x,$
so from the latter one may refer to the
![]() $\alpha $
-regular conjugacy classes of
$\alpha $
-regular conjugacy classes of
![]() $G.$
$G.$
Definition 2.3. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of
$2$
-cocycle of
![]() $G.$
Then an
$G.$
Then an
![]() $\alpha $
-representation of G of dimension n is a function
$\alpha $
-representation of G of dimension n is a function
![]() $P:G\rightarrow \mathrm {GL}(n, \mathbb {C})$
such that
$P:G\rightarrow \mathrm {GL}(n, \mathbb {C})$
such that
![]() $P(x)P(y) = \alpha (x, y)P(xy)$
for all x,
$P(x)P(y) = \alpha (x, y)P(xy)$
for all x,
![]() $y\in G.$
$y\in G.$
Observe that if P is an
![]() $\alpha $
-representation of
$\alpha $
-representation of
![]() $G,$
then
$G,$
then
![]() $P(g)P(x)P(g)^{-1}\! =\! f_{\alpha }(g, x)P(gxg^{-1})$
and
$P(g)P(x)P(g)^{-1}\! =\! f_{\alpha }(g, x)P(gxg^{-1})$
and
![]() $P(x)^m = p_{\alpha }(x, m)P(x^m)$
for all
$P(x)^m = p_{\alpha }(x, m)P(x^m)$
for all
![]() $g, x\in G$
and
$g, x\in G$
and
![]() $m\in \mathbb {N},$
where
$m\in \mathbb {N},$
where
 $$ \begin{align*}f_{\alpha}(g, x) = \frac{\alpha(g, xg^{-1})\alpha(x, g^{-1})}{\alpha(g, g^{-1})} \quad \text{and} \quad p_{\alpha}(x, m) = \prod_{i=1}^{m-1}\alpha(x, x^i) \quad\text{for } m> 1.\end{align*} $$
$$ \begin{align*}f_{\alpha}(g, x) = \frac{\alpha(g, xg^{-1})\alpha(x, g^{-1})}{\alpha(g, g^{-1})} \quad \text{and} \quad p_{\alpha}(x, m) = \prod_{i=1}^{m-1}\alpha(x, x^i) \quad\text{for } m> 1.\end{align*} $$
An
![]() $\alpha $
-representation is also called a projective representation of G with
$\alpha $
-representation is also called a projective representation of G with
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
and its trace function is its
$\alpha $
and its trace function is its
![]() $\alpha $
-character. Let
$\alpha $
-character. Let
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
$\operatorname {\mathrm {Proj}}(G, \alpha )$
denote the set of all irreducible
![]() $\alpha $
-characters of G. The relationship between
$\alpha $
-characters of G. The relationship between
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\alpha $
-representations is much the same as that between
$\alpha $
-representations is much the same as that between
![]() $\operatorname {\mathrm {Irr}}(G)$
and ordinary representations of G (see [Reference Karpilovsky4, page 184] for details). Next
$\operatorname {\mathrm {Irr}}(G)$
and ordinary representations of G (see [Reference Karpilovsky4, page 184] for details). Next
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $\xi (x)\not = 0$
for some
$\xi (x)\not = 0$
for some
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
$\vert \!\operatorname {\mathrm {Proj}}(G, \alpha )\vert $
is the number of
![]() $\alpha $
-regular conjugacy classes of
$\alpha $
-regular conjugacy classes of
![]() $G.$
$G.$
For
![]() $[\beta ]\in M(G)$
there exists
$[\beta ]\in M(G)$
there exists
![]() $\alpha \in [\beta ]$
such that
$\alpha \in [\beta ]$
such that
![]() $o(\alpha ) = o([\beta ])$
and
$o(\alpha ) = o([\beta ])$
and
![]() $\alpha $
is a class-function
$\alpha $
is a class-function
![]() $2$
-cocycle, that is, the elements of
$2$
-cocycle, that is, the elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions. If
$\operatorname {\mathrm {Proj}}(G, \alpha )$
are class functions. If
![]() $\alpha $
is a class-function
$\alpha $
is a class-function
![]() $2$
-cocycle of G, then
$2$
-cocycle of G, then
![]() $x\in G$
is
$x\in G$
is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $f_{\alpha }(g, x) = 1$
for all
$f_{\alpha }(g, x) = 1$
for all
![]() $g\in G.$
$g\in G.$
The nth Frobenius–Schur indicator of
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
can now be defined and agrees with the normal definition if
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
can now be defined and agrees with the normal definition if
![]() $\alpha $
is trivial.
$\alpha $
is trivial.
Definition 2.4. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order. Then the nth Frobenius–Schur indicator
$2$
-cocycle of G of finite order. Then the nth Frobenius–Schur indicator
![]() $v_n^{\alpha }(\xi )$
for
$v_n^{\alpha }(\xi )$
for
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $n\in \mathbb {N}$
is given by
$n\in \mathbb {N}$
is given by
 $$ \begin{align*}v_n^{\alpha}(\xi) = \left\{\! \begin{array}{@{}ll} \displaystyle{\frac{1}{\vert G\vert}\sum_{x\in G}p_{\alpha}(x, n)\xi(x^n)} & \text{if}\ n\equiv 0\pmod{o(\alpha)} \\ 0 & \text{otherwise.} \end{array} \right.\end{align*} $$
$$ \begin{align*}v_n^{\alpha}(\xi) = \left\{\! \begin{array}{@{}ll} \displaystyle{\frac{1}{\vert G\vert}\sum_{x\in G}p_{\alpha}(x, n)\xi(x^n)} & \text{if}\ n\equiv 0\pmod{o(\alpha)} \\ 0 & \text{otherwise.} \end{array} \right.\end{align*} $$
If
![]() $\alpha $
is a
$\alpha $
is a
![]() $2$
-cocycle of finite order of
$2$
-cocycle of finite order of
![]() $G,$
then this allows the construction of the
$G,$
then this allows the construction of the
![]() $\alpha $
-covering group H of G (see [Reference Karpilovsky4, Ch. 4, Section 1] or [Reference Haggarty and Humphreys1, page 191]). Let
$\alpha $
-covering group H of G (see [Reference Karpilovsky4, Ch. 4, Section 1] or [Reference Haggarty and Humphreys1, page 191]). Let
![]() $\omega $
be a primitive
$\omega $
be a primitive
![]() $o(\alpha )$
th root of unity and let
$o(\alpha )$
th root of unity and let
![]() $A = \langle \omega \rangle .$
The set of elements of H may be taken to be
$A = \langle \omega \rangle .$
The set of elements of H may be taken to be
![]() $\{ar(x): a\in A, x\in G\}$
, and H is a group under the binary operation
$\{ar(x): a\in A, x\in G\}$
, and H is a group under the binary operation
![]() $ar(x)br(y) = ab\alpha (x, y)r(xy)$
for all
$ar(x)br(y) = ab\alpha (x, y)r(xy)$
for all
![]() $a, b\in A$
and all
$a, b\in A$
and all
![]() $x, y\in G.$
This is a central extension of G:
$x, y\in G.$
This is a central extension of G:
with
![]() $\pi (r(x) )= x$
for all
$\pi (r(x) )= x$
for all
![]() $x\in G.$
It also has the following important property. Let P be an
$x\in G.$
It also has the following important property. Let P be an
![]() $\alpha ^i$
-representation of G for
$\alpha ^i$
-representation of G for
![]() $i\in \mathbb {Z}$
. Then
$i\in \mathbb {Z}$
. Then
![]() $R(ar(x)) = \lambda ^i(a)P(x)$
for all
$R(ar(x)) = \lambda ^i(a)P(x)$
for all
![]() $a\in A$
and all
$a\in A$
and all
![]() $x\in G$
is an ordinary representation of
$x\in G$
is an ordinary representation of
![]() $H,$
where
$H,$
where
![]() $\lambda \in \operatorname {\mathrm {Lin}}(A)$
with
$\lambda \in \operatorname {\mathrm {Lin}}(A)$
with
![]() $\lambda (\omega ) = \omega ;$
moreover, P is irreducible if and only if R is. Here R is said to linearise P (or to be the lift of P). Let
$\lambda (\omega ) = \omega ;$
moreover, P is irreducible if and only if R is. Here R is said to linearise P (or to be the lift of P). Let
![]() $\operatorname {\mathrm {Irr}}(H\vert \lambda ^i) = \{\chi \in \operatorname {\mathrm {Irr}}(H): \chi _A = \chi (1)\lambda ^i\}$
for
$\operatorname {\mathrm {Irr}}(H\vert \lambda ^i) = \{\chi \in \operatorname {\mathrm {Irr}}(H): \chi _A = \chi (1)\lambda ^i\}$
for
![]() $i\in \mathbb {Z}.$
Then the linearisation process outlined means that for each such i there exists a bijection from
$i\in \mathbb {Z}.$
Then the linearisation process outlined means that for each such i there exists a bijection from
![]() $\operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
to
$\operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
to
![]() $\operatorname {\mathrm {Proj}}(G, \alpha ^i)$
defined by
$\operatorname {\mathrm {Proj}}(G, \alpha ^i)$
defined by
![]() $\chi \mapsto \xi ,$
where
$\chi \mapsto \xi ,$
where
![]() $\chi (r(x)) = \xi (x)$
for all
$\chi (r(x)) = \xi (x)$
for all
![]() $x\in G$
and it is convenient to say that
$x\in G$
and it is convenient to say that
![]() $\chi $
linearises
$\chi $
linearises
![]() $\xi $
.
$\xi $
.
Now x is
![]() $\alpha $
-regular if and only if
$\alpha $
-regular if and only if
![]() $\omega ^ir(x)$
and
$\omega ^ir(x)$
and
![]() $\omega ^jr(x)$
are not conjugate for all i and j with
$\omega ^jr(x)$
are not conjugate for all i and j with
![]() $0\leq i<j\leq o(\alpha )-1.$
So for counting purposes there are exactly
$0\leq i<j\leq o(\alpha )-1.$
So for counting purposes there are exactly
![]() $o(\alpha )$
conjugacy classes of H that map under
$o(\alpha )$
conjugacy classes of H that map under
![]() $\pi $
to the conjugacy class of an
$\pi $
to the conjugacy class of an
![]() $\alpha $
-regular element of G and fewer than this for an element that is not
$\alpha $
-regular element of G and fewer than this for an element that is not
![]() $\alpha $
-regular. If
$\alpha $
-regular. If
![]() $o(\alpha ) = o([\alpha ]),$
then
$o(\alpha ) = o([\alpha ]),$
then
![]() $A\leq H'$
and the mapping
$A\leq H'$
and the mapping
![]() $\alpha ^i\mapsto [\alpha ^i] = [\alpha ]^i$
for
$\alpha ^i\mapsto [\alpha ^i] = [\alpha ]^i$
for
![]() $i =0,\ldots , o(\alpha )-1$
is a bijection.
$i =0,\ldots , o(\alpha )-1$
is a bijection.
Lemma 2.5. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order and let H be the
$2$
-cocycle of G of finite order and let H be the
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
If
$G.$
If
![]() $r(x)\in H$
is real, then so too is
$r(x)\in H$
is real, then so too is
![]() $x.$
Conversely if
$x.$
Conversely if
![]() $x\in G$
is real, then
$x\in G$
is real, then
![]() $r(x)$
is real if and only if there exists
$r(x)$
is real if and only if there exists
![]() $g\in G$
such that
$g\in G$
such that
![]() $gxg^{-1} = x^{-1}$
and
$gxg^{-1} = x^{-1}$
and
![]() $f_{\alpha }(g, x) = \alpha (x, x^{-1})^{-1}.$
$f_{\alpha }(g, x) = \alpha (x, x^{-1})^{-1}.$
Proof. If
![]() $r(x)$
is real with
$r(x)$
is real with
![]() $r(g)r(x)r(g)^{-1} = r(x)^{-1},$
it follows that
$r(g)r(x)r(g)^{-1} = r(x)^{-1},$
it follows that
![]() $f_{\alpha }(g, x)r(gxg^{-1}) = \alpha (x, x^{-1})^{-1}r(x^{-1}),$
so that in particular
$f_{\alpha }(g, x)r(gxg^{-1}) = \alpha (x, x^{-1})^{-1}r(x^{-1}),$
so that in particular
![]() $gxg^{-1} = x^{-1}$
and x is real. The converse is now obvious.
$gxg^{-1} = x^{-1}$
and x is real. The converse is now obvious.
Lemma 2.6. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order and let H be the
$2$
-cocycle of G of finite order and let H be the
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
Let
$G.$
Let
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ^i)$
for
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ^i)$
for
![]() $i\in \mathbb {Z}$
and let
$i\in \mathbb {Z}$
and let
![]() $\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
linearise
$\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
linearise
![]() $\xi .$
Then
$\xi .$
Then
![]() $v_n^{\alpha ^i}(\xi ) = v_n(\chi ).$
$v_n^{\alpha ^i}(\xi ) = v_n(\chi ).$
Proof. Using the notation introduced,
![]() $r(x)^n = p_{\alpha }(x, n)r(x^n)$
for
$r(x)^n = p_{\alpha }(x, n)r(x^n)$
for
![]() $n\in \mathbb {N}.$
So from Theorem 1.1,
$n\in \mathbb {N}.$
So from Theorem 1.1,
 $$ \begin{align*} v_n(\chi) & = \frac{1}{\vert H\vert}\sum_{a\in A, x\in G}\chi(a^np_{\alpha}(x, n)r(x^n)) \\ & = \frac{1}{\vert H\vert}\sum_{a\in A, x\in G}\lambda^i(a^n)p_{\alpha^i}(x, n)\xi(x^n) = v_n(\lambda^i)v_n^{\alpha^i}(\xi) = v_n^{\alpha^i}(\xi), \end{align*} $$
$$ \begin{align*} v_n(\chi) & = \frac{1}{\vert H\vert}\sum_{a\in A, x\in G}\chi(a^np_{\alpha}(x, n)r(x^n)) \\ & = \frac{1}{\vert H\vert}\sum_{a\in A, x\in G}\lambda^i(a^n)p_{\alpha^i}(x, n)\xi(x^n) = v_n(\lambda^i)v_n^{\alpha^i}(\xi) = v_n^{\alpha^i}(\xi), \end{align*} $$
since
![]() $v_n(\lambda ^i) = v_1(\lambda ^{ni})$
from Theorem 1.1, so that
$v_n(\lambda ^i) = v_1(\lambda ^{ni})$
from Theorem 1.1, so that
![]() $v_n(\lambda ^i) =1$
if
$v_n(\lambda ^i) =1$
if
![]() $o(\lambda ^{ni}) = 1$
and is
$o(\lambda ^{ni}) = 1$
and is
![]() $0$
otherwise.
$0$
otherwise.
Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order and let H be the
$2$
-cocycle of G of finite order and let H be the
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
Consider another transversal of A in
$G.$
Consider another transversal of A in
![]() $H, \{s(x): x\in G\}$
with
$H, \{s(x): x\in G\}$
with
![]() $s(1) = 1,$
where
$s(1) = 1,$
where
![]() $s(x) = \delta (x)r(x)$
for
$s(x) = \delta (x)r(x)$
for
![]() $\delta (x)\in A.$
This gives rise to a new
$\delta (x)\in A.$
This gives rise to a new
![]() $2$
-cocycle
$2$
-cocycle
![]() $\beta \in [\alpha ]$
with
$\beta \in [\alpha ]$
with
![]() $\beta = t(\delta )\alpha $
and for which
$\beta = t(\delta )\alpha $
and for which
![]() $o(\beta )$
divides
$o(\beta )$
divides
![]() $o(\alpha ).$
Let
$o(\alpha ).$
Let
![]() $\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
. Then
$\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda ^i)$
. Then
![]() $\chi $
linearises
$\chi $
linearises
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ^i)$
and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ^i)$
and
![]() $\xi '\in \operatorname {\mathrm {Proj}}(G, \beta ^i),$
where
$\xi '\in \operatorname {\mathrm {Proj}}(G, \beta ^i),$
where
![]() $\xi '(x) = \lambda ^i(\delta (x))\xi (x)$
for all
$\xi '(x) = \lambda ^i(\delta (x))\xi (x)$
for all
![]() $x\in G.$
Now
$x\in G.$
Now
![]() $s(x)^n = r(x)^n$
for
$s(x)^n = r(x)^n$
for
![]() $n\equiv 0 \pmod {o(\alpha )}$
and so, from the proof of Lemma 2.6,
$n\equiv 0 \pmod {o(\alpha )}$
and so, from the proof of Lemma 2.6,
![]() $v_n^{\alpha ^i}(\xi ) = v_n^{\beta ^i}(\xi ')$
for
$v_n^{\alpha ^i}(\xi ) = v_n^{\beta ^i}(\xi ')$
for
![]() $n\equiv 0 \pmod {o(\alpha )}.$
If
$n\equiv 0 \pmod {o(\alpha )}.$
If
![]() $o(\alpha ) = o([\alpha ]),$
then
$o(\alpha ) = o([\alpha ]),$
then
![]() $o(\beta ) = o(\alpha )$
and H is also the
$o(\beta ) = o(\alpha )$
and H is also the
![]() $\beta $
-covering group of
$\beta $
-covering group of
![]() $G.$
$G.$
Using this notation,
![]() $\{s(x): x\in G\}$
can be chosen to be conjugacy-preserving, that is,
$\{s(x): x\in G\}$
can be chosen to be conjugacy-preserving, that is,
![]() $s(x)$
and
$s(x)$
and
![]() $s(y)$
are conjugate in H whenever x and y are conjugate in G (see [Reference Karpilovsky5, Lemma 4.1.1] or [Reference Haggarty and Humphreys1, Proposition 1.1]) and this choice makes
$s(y)$
are conjugate in H whenever x and y are conjugate in G (see [Reference Karpilovsky5, Lemma 4.1.1] or [Reference Haggarty and Humphreys1, Proposition 1.1]) and this choice makes
![]() $\beta $
a class-function
$\beta $
a class-function
![]() $2$
-cocycle.
$2$
-cocycle.
The next result is an immediate corollary of Lemma 2.6 from [Reference Isaacs3, page 58].
Corollary 2.7. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ) = o([\alpha ]) = 2.$
Let
$o(\alpha ) = o([\alpha ]) = 2.$
Let
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ).$
Then
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha ).$
Then
![]() $v_2^{\alpha }(\xi ) = 0$
or
$v_2^{\alpha }(\xi ) = 0$
or
![]() $\pm 1.$
Moreover,
$\pm 1.$
Moreover,
![]() $v_2^{\alpha }(\xi ) = 0$
if and only if
$v_2^{\alpha }(\xi ) = 0$
if and only if
![]() $\xi $
is nonreal,
$\xi $
is nonreal,
![]() $v_2^{\alpha }(\xi ) =1$
if and only if
$v_2^{\alpha }(\xi ) =1$
if and only if
![]() $\xi $
is afforded by a real
$\xi $
is afforded by a real
![]() $\alpha $
-representation, and
$\alpha $
-representation, and
![]() $v_2^{\alpha }(\xi ) = -1$
if and only if
$v_2^{\alpha }(\xi ) = -1$
if and only if
![]() $\xi $
is real but is not afforded by any real
$\xi $
is real but is not afforded by any real
![]() $\alpha $
-representation of
$\alpha $
-representation of
![]() $G.$
$G.$
Lemma 2.6 also explains why the second Frobenius–Schur indicator is defined to be
![]() $0$
when
$0$
when
![]() $o(\alpha )> 2,$
but another rationale follows. If
$o(\alpha )> 2,$
but another rationale follows. If
![]() $\alpha (x, y)\not \in \mathbb {R}$
and P is an
$\alpha (x, y)\not \in \mathbb {R}$
and P is an
![]() $\alpha $
-representation of
$\alpha $
-representation of
![]() $G,$
then at least one of the three matrices
$G,$
then at least one of the three matrices
![]() $P(x), P(y)$
and
$P(x), P(y)$
and
![]() $P(xy)$
must contain a nonreal entry.
$P(xy)$
must contain a nonreal entry.
Example 2.8. Consider the elementary abelian group
![]() $G = C_p\times C_p$
for p a prime number, which has
$G = C_p\times C_p$
for p a prime number, which has
![]() $M(G)\cong C_p$
(see [Reference Karpilovsky4, Proposition 10.7.1]). Let
$M(G)\cong C_p$
(see [Reference Karpilovsky4, Proposition 10.7.1]). Let
![]() $\alpha $
be any
$\alpha $
be any
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o([\alpha ]) = p.$
Then the only
$o([\alpha ]) = p.$
Then the only
![]() $\alpha $
-regular element of G is the identity element and consequently the only element
$\alpha $
-regular element of G is the identity element and consequently the only element
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
has
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
has
![]() $\xi (1) = p$
and
$\xi (1) = p$
and
![]() $\xi (x) = 0$
for
$\xi (x) = 0$
for
![]() $x\ne 1$
(see [Reference Karpilovsky5, Theorem 8.2.21]). So
$x\ne 1$
(see [Reference Karpilovsky5, Theorem 8.2.21]). So
![]() $\xi $
is integer-valued, but is not afforded by any real
$\xi $
is integer-valued, but is not afforded by any real
![]() $\alpha $
-representation for
$\alpha $
-representation for
![]() $p\geq 3$
from the remark preceding this example. If
$p\geq 3$
from the remark preceding this example. If
![]() $o(\alpha )\geq 3$
and is finite, let H be the
$o(\alpha )\geq 3$
and is finite, let H be the
![]() $\alpha $
-covering group of G and let
$\alpha $
-covering group of G and let
![]() $\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda )$
linearise
$\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda )$
linearise
![]() $\xi .$
Then
$\xi .$
Then
![]() $\chi $
is nonreal since
$\chi $
is nonreal since
![]() $\lambda $
is nonreal.
$\lambda $
is nonreal.
It can be concluded from Example 2.8 that the results of Corollary 2.7 do not hold in general for any group G with a
![]() $2$
-cocycle of finite order greater than
$2$
-cocycle of finite order greater than
![]() $2$
and in this case
$2$
and in this case
![]() $v_2^{\alpha }(\xi ) = 0$
for all
$v_2^{\alpha }(\xi ) = 0$
for all
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
can only be interpreted as meaning that each
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
can only be interpreted as meaning that each
![]() $\xi $
is not afforded by any real
$\xi $
is not afforded by any real
![]() $\alpha $
-representation of
$\alpha $
-representation of
![]() $G.$
$G.$
It should be noted that in general the value of
![]() $v_n^{\alpha }(\xi )$
for
$v_n^{\alpha }(\xi )$
for
![]() $n\equiv 0\pmod {o(\alpha )}$
depends upon the choice of
$n\equiv 0\pmod {o(\alpha )}$
depends upon the choice of
![]() $\alpha $
, even if
$\alpha $
, even if
![]() $o(\alpha ) = o([\alpha ]) =2$
, as the next example illustrates.
$o(\alpha ) = o([\alpha ]) =2$
, as the next example illustrates.
Example 2.9. Let
![]() $G = C_2\times C_2.$
It is well known that G has two Schur representation groups (also known as covering groups) up to isomorphism, namely D and Q, the dihedral and quaternion groups of order
$G = C_2\times C_2.$
It is well known that G has two Schur representation groups (also known as covering groups) up to isomorphism, namely D and Q, the dihedral and quaternion groups of order
![]() $8$
, respectively. The character tables of these two groups are identical, and the irreducible characters
$8$
, respectively. The character tables of these two groups are identical, and the irreducible characters
![]() $\chi $
and
$\chi $
and
![]() $\chi '$
of degree
$\chi '$
of degree
![]() $2$
of each linearise
$2$
of each linearise
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\xi '\in \operatorname {\mathrm {Proj}}(G, \alpha ')$
respectively, where
$\xi '\in \operatorname {\mathrm {Proj}}(G, \alpha ')$
respectively, where
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are the
$\alpha '$
are the
![]() $2$
-cocycles of G constructed from D and Q of order
$2$
-cocycles of G constructed from D and Q of order
![]() $2$
with
$2$
with
![]() $o([\alpha ]) = o([\alpha ']) = 2.$
Now
$o([\alpha ]) = o([\alpha ']) = 2.$
Now
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
are identical and integer-valued from Example 2.8; however,
$\xi '$
are identical and integer-valued from Example 2.8; however,
![]() $v_2^{\alpha }(\xi ) = v_2(\chi ) = 1,$
whereas
$v_2^{\alpha }(\xi ) = v_2(\chi ) = 1,$
whereas
![]() $v_2^{\alpha '}(\xi ') = v_2(\chi ') = -1.$
$v_2^{\alpha '}(\xi ') = v_2(\chi ') = -1.$
Using Lemma 2.6 other results concerning
![]() $v_n$
carry over to
$v_n$
carry over to
![]() $v_n^{\alpha },$
as in the next lemma.
$v_n^{\alpha },$
as in the next lemma.
Lemma 2.10. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order. Let
$2$
-cocycle of G of finite order. Let
![]() $\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and let
$\xi \in \operatorname {\mathrm {Proj}}(G, \alpha )$
and let
![]() $\mu \in \operatorname {\mathrm {Lin}}(G)$
with
$\mu \in \operatorname {\mathrm {Lin}}(G)$
with
![]() $\mu ^n$
trivial for
$\mu ^n$
trivial for
![]() $n\in \mathbb {N}.$
Then
$n\in \mathbb {N}.$
Then
![]() $v_n^{\alpha }(\xi )\in \mathbb {Z}$
and
$v_n^{\alpha }(\xi )\in \mathbb {Z}$
and
![]() $v_n^{\alpha }(\mu \xi ) = v_n^{\alpha }(\xi ).$
$v_n^{\alpha }(\mu \xi ) = v_n^{\alpha }(\xi ).$
Proof. Let H be the
![]() $\alpha $
-covering group of G and
$\alpha $
-covering group of G and
![]() $\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda )$
linearise
$\chi \in \operatorname {\mathrm {Irr}}(H\vert \lambda )$
linearise
![]() $\xi $
. Then
$\xi $
. Then
![]() $v_n^{\alpha }(\xi )\in \mathbb {Z}$
from Lemma 2.6 and Theorem 1.1. Now let
$v_n^{\alpha }(\xi )\in \mathbb {Z}$
from Lemma 2.6 and Theorem 1.1. Now let
![]() $\nu \in \operatorname {\mathrm {Lin}}(H)$
linearise
$\nu \in \operatorname {\mathrm {Lin}}(H)$
linearise
![]() $\mu .$
Then
$\mu .$
Then
![]() $\nu \chi $
linearises
$\nu \chi $
linearises
![]() $\mu \xi $
and
$\mu \xi $
and
![]() $\nu ^n$
is trivial, so
$\nu ^n$
is trivial, so
![]() $v_n^{\alpha }(\mu \xi ) = v_n(\nu \chi ) = v_n(\chi ) = v_n^{\alpha }(\xi )$
using [Reference Isaacs3, Lemma 4.8] and Lemma 2.6.
$v_n^{\alpha }(\mu \xi ) = v_n(\nu \chi ) = v_n(\chi ) = v_n^{\alpha }(\xi )$
using [Reference Isaacs3, Lemma 4.8] and Lemma 2.6.
3 Frobenius–Schur indicator applications
Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G of finite order and define
$2$
-cocycle of G of finite order and define
 $$ \begin{align*} \theta_n^{\alpha} = \sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)}v_n^{\alpha}(\xi)\xi. \end{align*} $$
$$ \begin{align*} \theta_n^{\alpha} = \sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)}v_n^{\alpha}(\xi)\xi. \end{align*} $$
From Lemma 2.10,
![]() $\theta _n^{\alpha }$
is an integral linear combination of
$\theta _n^{\alpha }$
is an integral linear combination of
![]() $\alpha $
-characters of G and so
$\alpha $
-characters of G and so
![]() $\theta _n^{\alpha }(x) = 0$
if x is not
$\theta _n^{\alpha }(x) = 0$
if x is not
![]() $\alpha $
-regular. If, in addition,
$\alpha $
-regular. If, in addition,
![]() $\alpha $
is a class-function
$\alpha $
is a class-function
![]() $2$
-cocycle, then
$2$
-cocycle, then
![]() $\theta _n^{\alpha }$
is a class function. If
$\theta _n^{\alpha }$
is a class function. If
![]() $o(\alpha ) = 1,$
then
$o(\alpha ) = 1,$
then
![]() $\theta _n^{\alpha } = \theta _n$
as in Theorem 1.1.
$\theta _n^{\alpha } = \theta _n$
as in Theorem 1.1.
By analogy with the definition in Theorem 1.1, define
![]() $\theta _n^+: G\rightarrow \mathbb {Z}_{\geq 0}$
by
$\theta _n^+: G\rightarrow \mathbb {Z}_{\geq 0}$
by
for
![]() $n\in \mathbb {N}$
. This function is used in the generalisation of Theorem 1.1.
$n\in \mathbb {N}$
. This function is used in the generalisation of Theorem 1.1.
Theorem 3.1. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ) = o([\alpha ])$
of finite order m and let
$o(\alpha ) = o([\alpha ])$
of finite order m and let
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n\equiv 0\pmod {m}.$
Then
$n\equiv 0\pmod {m}.$
Then
 $$ \begin{align*}\sum_{i=1}^{m-1}\theta_n^{\alpha^i} = m\theta_n^+ - \theta_n.\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{m-1}\theta_n^{\alpha^i} = m\theta_n^+ - \theta_n.\end{align*} $$
Proof. Let H be the
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
Then, using Theorem 1.1 and Lemma 2.6,
$G.$
Then, using Theorem 1.1 and Lemma 2.6,
 $$ \begin{align*} \theta_n(r(x)) &= m\vert\{g\in G: p_{\alpha}(g, n) = 1\ \text{and}\ g^n = x\}\vert \\ &= \sum_{\chi\in\operatorname{\mathrm{Irr}}(H)} v_n(\chi)\chi(r(x)) = \sum_{\psi\in\operatorname{\mathrm{Irr}}(G)} v_n(\psi)\psi(x) + \sum_{i= 1}^{m-1}\sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha^i)} v_n^{\alpha^i}(\xi)\xi(x) \\ &= \theta_n(x) + \sum_{i=1}^{m-1}\theta_n^{\alpha^i}(x) \end{align*} $$
$$ \begin{align*} \theta_n(r(x)) &= m\vert\{g\in G: p_{\alpha}(g, n) = 1\ \text{and}\ g^n = x\}\vert \\ &= \sum_{\chi\in\operatorname{\mathrm{Irr}}(H)} v_n(\chi)\chi(r(x)) = \sum_{\psi\in\operatorname{\mathrm{Irr}}(G)} v_n(\psi)\psi(x) + \sum_{i= 1}^{m-1}\sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha^i)} v_n^{\alpha^i}(\xi)\xi(x) \\ &= \theta_n(x) + \sum_{i=1}^{m-1}\theta_n^{\alpha^i}(x) \end{align*} $$
for all
![]() $x\in G.$
$x\in G.$
Continuing with the notation and hypotheses in Theorem 3.1, suppose
![]() $g\in G$
with
$g\in G$
with
![]() $g^n = x$
and let
$g^n = x$
and let
![]() $y\in C_G(x).$
Then
$y\in C_G(x).$
Then
Now if m is a prime number and x is not
![]() $\alpha $
-regular, then
$\alpha $
-regular, then
![]() $r(x)$
is conjugate to
$r(x)$
is conjugate to
![]() $ar(x)$
for all
$ar(x)$
for all
![]() $a\in A.$
So if
$a\in A.$
So if
![]() $r(y)r(x)r(y)^{-1} = ar(x),$
then the mapping
$r(y)r(x)r(y)^{-1} = ar(x),$
then the mapping
![]() $g\mapsto ygy^{-1}$
defines a bijection from
$g\mapsto ygy^{-1}$
defines a bijection from
![]() $\{g\in G: p_{\alpha }(g, n) = 1~ \text {and}~g^n = x\}$
to
$\{g\in G: p_{\alpha }(g, n) = 1~ \text {and}~g^n = x\}$
to
![]() $\{g\in G: p_{\alpha }(g, n) = a~ \text {and}~g^n = x\},$
which explains why
$\{g\in G: p_{\alpha }(g, n) = a~ \text {and}~g^n = x\},$
which explains why
![]() $m\theta _n^+(x) = \theta _n(x)$
in this scenario.
$m\theta _n^+(x) = \theta _n(x)$
in this scenario.
The next result is a special case of Theorem 3.1 that generalises Corollary 1.2.
Corollary 3.2. Let
![]() $\alpha $
be a
$\alpha $
be a
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ) = o([\alpha ]) = 2.$
Let H be the
$o(\alpha ) = o([\alpha ]) = 2.$
Let H be the
![]() $\alpha $
-covering group of G and let H and G have exactly t and s involutions, respectively. Then
$\alpha $
-covering group of G and let H and G have exactly t and s involutions, respectively. Then
 $$ \begin{align*}t-s = \sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)} v_2^{\alpha}(\xi)\xi(1).\end{align*} $$
$$ \begin{align*}t-s = \sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)} v_2^{\alpha}(\xi)\xi(1).\end{align*} $$
Proof. Using Corollary 1.2 and the proof of Theorem 3.1,
 $$ \begin{align*}\sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)} v_2^{\alpha}(\xi)\xi(1) = \theta_2(r(1)) - \theta_2(1) = t -s.\\[-45pt] \end{align*} $$
$$ \begin{align*}\sum_{\xi\in\operatorname{\mathrm{Proj}}(G, \alpha)} v_2^{\alpha}(\xi)\xi(1) = \theta_2(r(1)) - \theta_2(1) = t -s.\\[-45pt] \end{align*} $$
The final aim is to generalise Theorem 1.3, which involves an analysis of the real conjugacy classes of
![]() $G.$
$G.$
Lemma 3.3. Let
![]() $\alpha $
be a class-function
$\alpha $
be a class-function
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ) = o([\alpha ]) = 2.$
Let H be the
$o(\alpha ) = o([\alpha ]) = 2.$
Let H be the
![]() $\alpha $
-covering group of G with its associated central subgroup
$\alpha $
-covering group of G with its associated central subgroup
![]() $A = \langle -1\rangle $
and transversal
$A = \langle -1\rangle $
and transversal
![]() $\{r(x): x\in G\}.$
Let
$\{r(x): x\in G\}.$
Let
![]() $x\in G$
be real. Then
$x\in G$
be real. Then
![]() $r(x)$
is nonreal if and only if x is
$r(x)$
is nonreal if and only if x is
![]() $\alpha $
-regular and
$\alpha $
-regular and
![]() $\alpha (x, x^{-1}) = -1.$
$\alpha (x, x^{-1}) = -1.$
Proof. If x is
![]() $\alpha $
-regular, then
$\alpha $
-regular, then
![]() $r(x)$
is real if and only if
$r(x)$
is real if and only if
![]() $\alpha (x, x^{-1}) = 1$
from Lemma 2.5. On the other hand, if x is not
$\alpha (x, x^{-1}) = 1$
from Lemma 2.5. On the other hand, if x is not
![]() $\alpha $
-regular, then there exists
$\alpha $
-regular, then there exists
![]() $y\in C_G(x)$
such that
$y\in C_G(x)$
such that
![]() $r(y)r(x^{-1})r(y)^{-1} = -r(x^{-1}).$
Now if
$r(y)r(x^{-1})r(y)^{-1} = -r(x^{-1}).$
Now if
![]() $gxg^{-1} = x^{-1},$
then either
$gxg^{-1} = x^{-1},$
then either
![]() $f_{\alpha }(g, x)$
or
$f_{\alpha }(g, x)$
or
![]() $f_{\alpha }(yg, x)$
equals
$f_{\alpha }(yg, x)$
equals
![]() $\alpha (x, x^{-1})^{-1}$
and so
$\alpha (x, x^{-1})^{-1}$
and so
![]() $r(x)$
is real from Lemma 2.5.
$r(x)$
is real from Lemma 2.5.
Let P be an
![]() $\alpha $
-representation of G of dimension
$\alpha $
-representation of G of dimension
![]() $n.$
Then for all
$n.$
Then for all
![]() $g, x\in G$
,
$g, x\in G$
,
![]() $P(g)P(x)P(x^{-1})P(g)^{-1}$
equals
$P(g)P(x)P(x^{-1})P(g)^{-1}$
equals
![]() $f_{\alpha }(g, x)f_{\alpha }(g, x^{-1})\alpha (gxg^{-1}, gx^{-1}g^{-1})I_n,$
but it also equals
$f_{\alpha }(g, x)f_{\alpha }(g, x^{-1})\alpha (gxg^{-1}, gx^{-1}g^{-1})I_n,$
but it also equals
![]() $\alpha (x, x^{-1})I_n.$
Thus if
$\alpha (x, x^{-1})I_n.$
Thus if
![]() $\alpha $
is a class-function
$\alpha $
is a class-function
![]() $2$
-cocycle of G and x is
$2$
-cocycle of G and x is
![]() $\alpha $
-regular, then
$\alpha $
-regular, then
![]() $\alpha (x, x^{-1}) = \alpha (gxg^{-1}, gx^{-1}g^{-1})$
for all
$\alpha (x, x^{-1}) = \alpha (gxg^{-1}, gx^{-1}g^{-1})$
for all
![]() $g\in G.$
In the context of Lemma 3.3 and using this result, let
$g\in G.$
In the context of Lemma 3.3 and using this result, let
![]() $k_0, k^+$
and
$k_0, k^+$
and
![]() $k^-$
denote the number of conjugacy classes
$k^-$
denote the number of conjugacy classes
![]() $\mathcal {C}$
of G that are respectively (a) real and not
$\mathcal {C}$
of G that are respectively (a) real and not
![]() $\alpha $
-regular, (b) real and
$\alpha $
-regular, (b) real and
![]() $\alpha $
-regular with
$\alpha $
-regular with
![]() $\alpha (x, x^{-1}) = 1$
for all
$\alpha (x, x^{-1}) = 1$
for all
![]() $x\in \mathcal {C},$
and (c) real and
$x\in \mathcal {C},$
and (c) real and
![]() $\alpha $
-regular with
$\alpha $
-regular with
![]() $\alpha (x, x^{-1}) = -1$
for all
$\alpha (x, x^{-1}) = -1$
for all
![]() $x\in \mathcal {C}.$
$x\in \mathcal {C}.$
Theorem 3.4. Let
![]() $\alpha $
be a class-function
$\alpha $
be a class-function
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ) = o([\alpha ]) = 2.$
Then the number of real elements of
$o(\alpha ) = o([\alpha ]) = 2.$
Then the number of real elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
is
$\operatorname {\mathrm {Proj}}(G, \alpha )$
is
![]() $k^+ - k^-.$
$k^+ - k^-.$
Proof. Let H be the
![]() $\alpha $
-covering group of
$\alpha $
-covering group of
![]() $G.$
The number of real conjugacy classes of G and H is
$G.$
The number of real conjugacy classes of G and H is
![]() $k_0 + k^+ + k^-$
and
$k_0 + k^+ + k^-$
and
![]() $k_0 + 2k^+$
, respectively, from Lemma 3.3 and previous remarks. Thus from Theorem 1.3 the number of real elements of
$k_0 + 2k^+$
, respectively, from Lemma 3.3 and previous remarks. Thus from Theorem 1.3 the number of real elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
is the second number minus the first.
$\operatorname {\mathrm {Proj}}(G, \alpha )$
is the second number minus the first.
If
![]() $\alpha '$
is a
$\alpha '$
is a
![]() $2$
-cocycle of G with
$2$
-cocycle of G with
![]() $o(\alpha ') = o([\alpha ']) = 2,$
then we may let H be the
$o(\alpha ') = o([\alpha ']) = 2,$
then we may let H be the
![]() $\alpha '$
-covering group of
$\alpha '$
-covering group of
![]() $G.$
As explained after Lemma 2.6: (a) there exists a change of transversal so that the resultant
$G.$
As explained after Lemma 2.6: (a) there exists a change of transversal so that the resultant
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
of G is a class-function
$\alpha $
of G is a class-function
![]() $2$
-cocycle with
$2$
-cocycle with
![]() $o(\alpha ) = 2$
and
$o(\alpha ) = 2$
and
![]() $\alpha \in [\alpha '];$
(b) the numbers of real elements of
$\alpha \in [\alpha '];$
(b) the numbers of real elements of
![]() $\operatorname {\mathrm {Proj}}(G, \alpha )$
and
$\operatorname {\mathrm {Proj}}(G, \alpha )$
and
![]() $\operatorname {\mathrm {Proj}}(G, \alpha ')$
are equal, with this number given by Theorem 3.4.
$\operatorname {\mathrm {Proj}}(G, \alpha ')$
are equal, with this number given by Theorem 3.4.
Example 3.5. Every element of the symmetric group
![]() $S_4$
is real,
$S_4$
is real,
![]() $M(S_4)\cong C_2$
and
$M(S_4)\cong C_2$
and
![]() $S_4$
has two Schur representation groups up to isomorphism (see [Reference Morris6, Theorem 1]). One is the binary octahedral group, and the three elements of
$S_4$
has two Schur representation groups up to isomorphism (see [Reference Morris6, Theorem 1]). One is the binary octahedral group, and the three elements of
![]() $\operatorname {\mathrm {Proj}}(S_4, \alpha )$
constructed from this group, for a class-function
$\operatorname {\mathrm {Proj}}(S_4, \alpha )$
constructed from this group, for a class-function
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha $
with
$\alpha $
with
![]() $o(\alpha ) = o([\alpha ]) = 2,$
are all real (see [Reference Morris6, page 70]), so
$o(\alpha ) = o([\alpha ]) = 2,$
are all real (see [Reference Morris6, page 70]), so
![]() $k^+ = 3$
and
$k^+ = 3$
and
![]() $k^- = 0.$
The other Schur representation group is
$k^- = 0.$
The other Schur representation group is
![]() $\mathrm {GL}(2, 3)$
, and only one element of
$\mathrm {GL}(2, 3)$
, and only one element of
![]() $\operatorname {\mathrm {Proj}}(S_4, \alpha ')$
constructed from this group, for a class-function
$\operatorname {\mathrm {Proj}}(S_4, \alpha ')$
constructed from this group, for a class-function
![]() $2$
-cocycle
$2$
-cocycle
![]() $\alpha '$
with
$\alpha '$
with
![]() $o(\alpha ') = 2$
and
$o(\alpha ') = 2$
and
![]() $\alpha '\in [\alpha ],$
is real (see [Reference Humphreys2, Remark (ii), pages 27–28] or [Reference Morris6, page 56]), so here
$\alpha '\in [\alpha ],$
is real (see [Reference Humphreys2, Remark (ii), pages 27–28] or [Reference Morris6, page 56]), so here
![]() $k^+ = 2$
and
$k^+ = 2$
and
![]() $k^- = 1.$
$k^- = 1.$