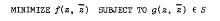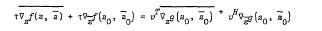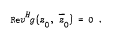Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Craven, B.D
and
Mond, B
1973.
Real and complex Fritz John theorems.
Journal of Mathematical Analysis and Applications,
Vol. 44,
Issue. 3,
p.
773.
Gulati, T.R.
1974.
A Fritz John type sufficient optimality theorem in complex space.
Bulletin of the Australian Mathematical Society,
Vol. 11,
Issue. 2,
p.
219.
Craven, B.D.
1975.
Sufficient Fritz John optimality conditions.
Bulletin of the Australian Mathematical Society,
Vol. 13,
Issue. 3,
p.
411.
Borwein, J.M.
1976.
A note on Fritz John sufficiency.
Bulletin of the Australian Mathematical Society,
Vol. 15,
Issue. 2,
p.
293.
Alders, C.D.
and
Sposito, V.A.
1977.
On a sufficient optimality condition over convex feasible regions.
Bulletin of the Australian Mathematical Society,
Vol. 16,
Issue. 2,
p.
199.
Craven, B. D.
1978.
Mathematical Programming and Control Theory.
p.
91.
Alders, D.C
and
Sposito, V.A
1979.
A note on “real and complex Fritz John theorems”.
Journal of Mathematical Analysis and Applications,
Vol. 67,
Issue. 1,
p.
92.
Das, C.
1979.
A Duality Theory of a General Class of Nonlinear Complex Programming.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 59,
Issue. 9,
p.
484.
Gulati, T. R.
1982.
On Nonlinear Nondifferentiable Complex Programming Problems.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 62,
Issue. 8,
p.
418.
Datta, Neelam
and
Bhatia, Davinder
1984.
Duality for a class of nondifferentiable mathematical programming problems in complex space.
Journal of Mathematical Analysis and Applications,
Vol. 101,
Issue. 1,
p.
1.
Youness, E.A
and
Elbrolosy, M.E
2004.
Extension to necessary optimality conditions in complex programming.
Applied Mathematics and Computation,
Vol. 154,
Issue. 1,
p.
229.