Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T08:32:37.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions of continuous functions: reflective functors

Published online by Cambridge University Press:  17 April 2009

W. N. Hunsaker  and
S. A. Naimpally
W. N. Hunsaker
Affiliation:
Department of Mathematics, Southern Illinois, University at Carbondale, Carbondale, Illinois 62901, United States of America
S. A. Naimpally
Affiliation:
Department of Mathematicsl Sciences, Lakehead University, Thunder Bay, Ontario, P7B 5E1, Canada.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to develop a general technique for attacking problems involving extensions of continuous functions from dense subspaces and to use it to obtain new results as well as to improve some of the known ones. The theory of structures developed by Harris is used to get some general results relating filters and covers. A necessary condition is derived for a continuous function f: X → Y to have a continuous extension 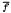: λx → λy where λZ denotes a given extension of the space Z. In the case of simple extensions, 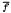is continuous and in the case of strict extensions 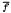is θ-continuous. In the case of strict extensions, sufficient conditions for uniqueness of 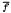are derived. These results are then applied to several extensions considered by Banaschewski, Fomin, Kat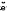tov, Liu-Strecker, Blaszczyk-Mioduszewski, Rudölf, etc.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 35 , Issue 3 , June 1987 , pp. 455 - 470
Copyright
Copyright © Australian Mathematical Society 1987

References

[1]Alo, R.A. and Shapiro, H.L., “L-realcompactifications and normal bases”, J. Austral. Math. Soc. 9 (1969), 489–495.CrossRefGoogle Scholar
[2]Banaschewski, B., “Uber Hausdorffsch-minimale Erweiterungen von Räumen”, Arch. Math. 12 (1961), 355–365.CrossRefGoogle Scholar
[3]Banaschewski, B., “Extensions of topological spaces”, Canad. Math. Bull. 7 (1964), 1–22.CrossRefGoogle Scholar
[4]Bentley, H.L. and Naimpally, S.A., “Wallman T1-compactification as epireflections”, General Topology and Appl. 4 (1974), 29–41.CrossRefGoogle Scholar
[5]Blaszczyk, A. and Miodusczewski, J., “On factorization of maps through τX”, Colloq. Math. 23 (1971), 45–52.CrossRefGoogle Scholar
[6]Chattopadhyay, K.C. and Njastad, Olav, “Quasi-regular nearness spaces and extensions of nearness-preserving maps”, Pacific J. Math. 105 (1983), 33–51.CrossRefGoogle Scholar
[7]Chattopadhyay, K.C. and Njastad, Olav, “Completion of merotopic spaces and extension of uniformly continuous maps”, Topology Appl. 15 (1983), 29–44.CrossRefGoogle Scholar
[8]Fan, K. and Gottesman, N., “On compactifications of Freudenthal and wallman”, Indag. Math. 14 (1952), 504–510.CrossRefGoogle Scholar
[9]Formin, S.V., “Extensions of topological spaces”, Ann. of Math. 44 (1943), 471–480.CrossRefGoogle Scholar
[10]Frolik, Z., “A generalization of realcompact spaces”, Czechoslovak Math. J. 13 (88) (1963), 127–138.CrossRefGoogle Scholar
[11]Gagrat, M.S. and Naimpally, S.A., “Proximity approach to extension problems”, Fund. Math. 71 (1971), 63–76.CrossRefGoogle Scholar
[12]Harris, D., “Structures in topology”, Mem. Amer. Math. Soc. 115 (1971), 1–96.Google Scholar
[13]Harris, D., “Katetov extension as a functor”, Math. Ann. 193 (1971), 171–175.CrossRefGoogle Scholar
[14]Harris, D., “The Wallman compactification is an epireflection”, Proc. Amer. Math. Soc. 31 (1972), 265–267.CrossRefGoogle Scholar
[15]Harris, D., “The Wallman compactification as a functor”, General Topology and Appl. 1 (1971), 273–281.CrossRefGoogle Scholar
[16]Herrlich, H., “Categorical topoloby”, General Topology and Appl. 1 (1971), 1–15.CrossRefGoogle Scholar
[17]Herlich, H., “On the concept of reflections in general topology”, in Contrib. Extens. Theory Topol. Struct. (VEB Deutscher Verlag der Wiss. Berlin, 1969), 105–114.Google Scholar
[18]Herrlich, H., “A concept of nearness”, General Topology and Appl. 4 (1974), 191–212.CrossRefGoogle Scholar
[19]Herrlich, H., “On the extendibility of continuous functions”, General Topology and Appl. 4 (1974), 213–215.CrossRefGoogle Scholar
[20]Herrlich, H. and Strecker, G., “H-closed spaces and reflective subcategories”, Math. Ann. 177 (1968), 302–309.CrossRefGoogle Scholar
[21]Hunsaker, W.N. and Naimpally, S.A., “Hausdorff compactifications as epireflections”, Canad. Math. Bull. 17 (5) (1975), 675–677.CrossRefGoogle Scholar
[22]Katětov, M., “On H-closed extensions of topological spaces”, Casopis Matem. Fys. 69 (1940), 36–49.CrossRefGoogle Scholar
[23]Liu, C.T., “The α-closure αx of a topological space X”, Proc. Amer. Math. Soc. 22 (1969), 620–624.Google Scholar
[24]Liu, C.T. and Strecker, G.E., “Concerning almost real-compactifications”, Czechoslovak. Math. J. 22 (1972), 181–190.CrossRefGoogle Scholar
[25]Mioduszewski, J. and Rudolf, L., “H-closed and extremally disconnected Hausdorff spaces”, Dissertationes Math. Rozprawy Mat. 66 (1969), 1–52.Google Scholar
[26]Naimpally, S.A., “Reflective functors via nearness”. Fund. Math. 85 (1974), 245–255.CrossRefGoogle Scholar
[27]Naimpally, S.A. and Warrack, B.D., Proximity Spaces, (Cambridge Univ. Press, 1970).Google Scholar
[28]Rudolf, L., “θ-continuous extensions of maps on τX”, Fund. Math. 74 (1972), 111–131.CrossRefGoogle Scholar
[29]van der Slot, J., “A general realcompactification method” Fund. Math. 67 (1970), 255–263.CrossRefGoogle Scholar
[30]Steiner, E.F., “Wallman spaces and compactifications”, Fund. Math. 61 (1968), 295–304.CrossRefGoogle Scholar
[31]Strecker, G.E., “Epireflection operators vs. perfect morphisms and closed classes of epimorphisms”, Bull. Austral. Math. Soc. 7 (1972), 359–366.CrossRefGoogle Scholar
[32]Taimanov, A.D., “On extension of continuous mappings of topological spaces”. Mat. Sb. 31 (1952), 459–463.Google Scholar
[33]Velicko, W.V., “H-closed topological spaces”, American Mathematical Society Translations, Series 2 78 (1968), 103–118.Google Scholar