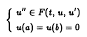Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Averna, Diego
and
Salvatore A., Marano
1999.
Existence theorems for inclusions of the type.
Applicable Analysis,
Vol. 72,
Issue. 3-4,
p.
449.
Halidias, Nikolaos
and
Papageorgiou, Nikolaos S.
2000.
Existence of solutions for quasilinear second order differential inclusions with nonlinear boundary conditions.
Journal of Computational and Applied Mathematics,
Vol. 113,
Issue. 1-2,
p.
51.
Castaing, Charles
and
Truong, Le Xuan
2012.
Some Topological Properties of Solution Sets in a Second Order Differential Inclusion with m-point Boundary Conditions.
Set-Valued and Variational Analysis,
Vol. 20,
Issue. 2,
p.
249.
Azzam-Laouir, Dalila
and
Boukrouk, Wafiya
2015.
A Delay Second-Order Set-Valued Differential Equation with Hukuhara Derivatives.
Numerical Functional Analysis and Optimization,
Vol. 36,
Issue. 6,
p.
704.
Candito, Pasquale
Livrea, Roberto
and
Sanchez, Luís
2025.
Existence and approximation of a solution for a two point nonlinear Dirichlet problem.
Discrete and Continuous Dynamical Systems - S,
Vol. 18,
Issue. 6,
p.
1540.