Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Andrade, Bruno
and
Cuevas, Claudio
2010.
-asymptotically -periodic and asymptotically -periodic solutions to semi-linear Cauchy problems with non-dense domain.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 6,
p.
3190.
Cuevas, Claudio
and
César de Souza, Julio
2010.
Existence of -asymptotically -periodic solutions for fractional order functional integro-differential equations with infinite delay.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 3-4,
p.
1683.
Lizama, Carlos
and
N’Guérékata, Gaston M.
2010.
Bounded Mild Solutions for Semilinear Integro Differential Equations in Banach Spaces.
Integral Equations and Operator Theory,
Vol. 68,
Issue. 2,
p.
207.
Hernández, Eduardo
Pierri, Michelle
and
Aparecida Bená, Maria
2011.
Asymptotically almost periodic solutions for abstract neutral integro-differential equations.
Applied Mathematics and Computation,
Vol. 217,
Issue. 22,
p.
8963.
Cuevas, Claudio
Pierri, Michelle
and
Sepulveda, Alex
2011.
Weighted S-Asymptotically ω-Periodic Solutions of a Class of Fractional Differential Equations.
Advances in Difference Equations,
Vol. 2011,
Issue. ,
p.
1.
Hernández, Eduardo M.
and
O’Regan, Donal
2011.
Existence of solutions for abstract neutral integro-differential equations with unbounded delay.
Czechoslovak Mathematical Journal,
Vol. 61,
Issue. 3,
p.
691.
Caicedo, Alejandro
Cuevas, Claudio
and
Henríquez, Hernán R.
2011.
Asymptotic Periodicity for a Class of Partial Integrodifferential Equations.
ISRN Mathematical Analysis,
Vol. 2011,
Issue. ,
p.
1.
Agarwal, Ravi P.
Cuevas, Claudio
Soto, Herme
and
El-Gebeily, Mohamed
2011.
Asymptotic periodicity for some evolution equations in Banach spaces.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 74,
Issue. 5,
p.
1769.
Agarwal, Ravi P.
Cuevas, Claudio
and
Frasson, Miguel V.S.
2012.
Semilinear functional difference equations with infinite delay.
Mathematical and Computer Modelling,
Vol. 55,
Issue. 3-4,
p.
1083.
Dimbour, William
and
N’Guérékata, Gaston M.
2012.
S-asymptotically ω-periodic solutions to some classes of partial evolution equations.
Applied Mathematics and Computation,
Vol. 218,
Issue. 14,
p.
7622.
Pierri, Michelle
2012.
On -asymptotically -periodic functions and applications.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 2,
p.
651.
Caicedo, A.
Cuevas, C.
Mophou, G.M.
and
N’Guérékata, G.M.
2012.
Asymptotic behavior of solutions of some semilinear functional differential and integro-differential equations with infinite delay in Banach spaces.
Journal of the Franklin Institute,
Vol. 349,
Issue. 1,
p.
1.
Henríquez, Hernán R.
2013.
Asymptotically periodic solutions of abstract differential equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 80,
Issue. ,
p.
135.
PIERRI, MICHELLE
and
ROLNIK, VANESSA
2013.
ON PSEUDO -ASYMPTOTICALLY PERIODIC FUNCTIONS.
Bulletin of the Australian Mathematical Society,
Vol. 87,
Issue. 2,
p.
238.
Lizama, Carlos
and
N'Guérékata, Gaston M.
2013.
Mild solutions for abstract fractional differential equations.
Applicable Analysis,
Vol. 92,
Issue. 8,
p.
1731.
Henríquez, Hernán R.
and
Cuevas, Claudio
2013.
Almost automorphy for abstract neutral differential equations via control theory.
Annali di Matematica Pura ed Applicata,
Vol. 192,
Issue. 3,
p.
393.
Henríquez, Hernán R.
Cuevas, Claudio
and
Caicedo, Alejandro
2013.
Asymptotically periodic solutions of neutral partial differential equations with infinite delay.
Communications on Pure and Applied Analysis,
Vol. 12,
Issue. 5,
p.
2031.
Xia, Zhinan
2014.
Asymptotically periodic solutions of semilinear fractional integro-differential equations.
Advances in Difference Equations,
Vol. 2014,
Issue. 1,
Cuevas, Claudio
Henríquez, Hernán R.
and
Soto, Herme
2014.
Asymptotically periodic solutions of fractional differential equations.
Applied Mathematics and Computation,
Vol. 236,
Issue. ,
p.
524.
Xia, Zhinan
2014.
Discrete Weighted Pseudo Asymptotic Periodicity of Second Order Difference Equations.
Discrete Dynamics in Nature and Society,
Vol. 2014,
Issue. ,
p.
1.


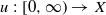 is said to be
is said to be 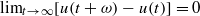 . This paper is devoted to study the existence and qualitative properties of
. This paper is devoted to study the existence and qualitative properties of 