Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ROYER, EMMANUEL
2007.
EVALUATING CONVOLUTION SUMS OF THE DIVISOR FUNCTION BY QUASIMODULAR FORMS.
International Journal of Number Theory,
Vol. 03,
Issue. 02,
p.
231.
Xia, Ernest X. W.
Yao, Olivia X. M.
and
Hartung, Ferenc
2012.
Eisenstein Series Identities Involving the Borweins′ Cubic Theta Functions.
Journal of Applied Mathematics,
Vol. 2012,
Issue. 1,
RAMAKRISHNAN, B.
and
SAHU, BRUNDABAN
2013.
EVALUATION OF THE CONVOLUTION SUMS ∑l+15m=nσ(l)σ(m) AND ∑3l+5m=nσ(l)σ(m) AND AN APPLICATION.
International Journal of Number Theory,
Vol. 09,
Issue. 03,
p.
799.
Cho, Bumkyu
Kim, Daeyeoul
and
Park, Ho
2013.
Evaluation of a certain combinatorial convolution sum in higher level cases.
Journal of Mathematical Analysis and Applications,
Vol. 406,
Issue. 1,
p.
203.
Xia, Ernest X. W.
Tian, X. L.
and
Yao, Olivia X. M.
2014.
Evaluation of the convolution sum ∑i+25j=n σ(i)σ(j).
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1421.
Cooper, Shaun
and
Ye, Dongxi
2014.
Evaluation of the convolution sums ∑l+20m=n σ(l)σ(m), ∑4l+5m=n σ(l)σ(m) and ∑2l+5m=n σ(l)σ(m).
International Journal of Number Theory,
Vol. 10,
Issue. 06,
p.
1385.
Ye, Dongxi
2015.
Evaluation of the convolution sums ∑l+36m=n σ(l)σ(m) and ∑4l+9m=n σ(l)σ(m).
International Journal of Number Theory,
Vol. 11,
Issue. 01,
p.
171.
Alaca, Şaban
and
Kesicioğlu, Yavuz
2016.
Evaluation of the convolution sums ∑l+27m=nσ(l)σ(m) and ∑l+32m=nσ(l)σ(m).
International Journal of Number Theory,
Vol. 12,
Issue. 01,
p.
1.
Park, Yoon Kyung
2016.
Evaluation of the convolution sums ∑++=σ(k)σ(l)σ(m) with lcm(a,b,c)≤6.
Journal of Number Theory,
Vol. 168,
Issue. ,
p.
257.
Ntienjem, Ebénézer
2017.
Evaluation of the convolution sum involving the sum of divisors function for 22, 44 and 52.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
446.
Lee, Joohee
and
Park, Yoon Kyung
2017.
Evaluation of the convolution sums ∑a1m1+a2m2+a3m3+a4m4=nσ(m1)σ(m2)σ(m3)σ(m4) with lcm(a1,a2,a3,a4) ≤ 4.
International Journal of Number Theory,
Vol. 13,
Issue. 08,
p.
2155.
Park, Yoon Kyung
2017.
Evaluation of the convolution sums ∑al+bm=n lσ(l) σ(m) with ab ≤ 9.
Open Mathematics,
Vol. 15,
Issue. 1,
p.
1389.
Park, Yoon Kyung
2018.
Evaluation of the convolution sums ∑ak+bl+cm=nσ(k)σ(l)σ(m) with lcm(a,b,c) = 7,8 or 9.
International Journal of Number Theory,
Vol. 14,
Issue. 06,
p.
1637.
Aygin, Zafer Selcuk
2019.
Eisenstein series and convolution sums.
The Ramanujan Journal,
Vol. 48,
Issue. 3,
p.
495.
Alaca, Şaban
and
Kesicioglu, Yavuz
2019.
Evaluation of the convolution sum $\sum_{al+bm=n} \sigma(l) \sigma(m)$ for $(a,b)=(1,48),(3,16),(1,54),(2,27)$.
Functiones et Approximatio Commentarii Mathematici,
Vol. 61,
Issue. 1,
Shruthi
and
Kumar, B. R. Srivatsa
2020.
Some new Eisenstein series containing the Borweins’ cubic theta functions and convolution sum $$\displaystyle {\sum _{i+4j=n}^{}\sigma (i)\sigma (j)}$$.
Afrika Matematika,
Vol. 31,
Issue. 5-6,
p.
971.
Cho, Bumkyu
2020.
Convolution sums of a divisor function for prime levels.
International Journal of Number Theory,
Vol. 16,
Issue. 03,
p.
537.
Köklüce, Bülent
2022.
Representations by certain octonary quadratic forms with coefficients 1, 2, 5 and 10.
Proceedings - Mathematical Sciences,
Vol. 132,
Issue. 2,
Pushpa, K.
and
Vasuki, K. R.
2022.
On Eisenstein series, color partition and divisor function.
Arabian Journal of Mathematics,
Vol. 11,
Issue. 2,
p.
355.
Pushpa, K.
and
Vasuki, K. R.
2022.
Evaluation of convolution sums $$\sum \limits _{l+15m=n} \sigma (l) \sigma (m)$$ and $$\sum \limits _{3l+5m=n} \sigma (l) \sigma (m)$$.
Indian Journal of Pure and Applied Mathematics,
Vol. 53,
Issue. 4,
p.
1110.


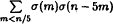 and
and  are evaluated for all
are evaluated for all 