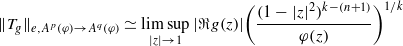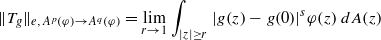Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tang, Xiaomin
2015.
Essential Norms of Weighted Composition Operators from Bloch-Type Space to $$H^\infty $$ H ∞ on the Unit Ball.
Complex Analysis and Operator Theory,
Vol. 9,
Issue. 1,
p.
229.


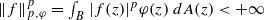 , where φ is a given normal weight. Let
, where φ is a given normal weight. Let 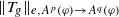 . In this paper it is proved that, for
. In this paper it is proved that, for