Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sun, Taixiang
2008.
On ω-limit sets of non-autonomous discrete systems on trees.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 68,
Issue. 4,
p.
781.
Sun, Taixiang
Xi, Hongjian
and
Chen, Zhanhuo
2008.
On topological entropy of commuting tree maps.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 69,
Issue. 1,
p.
167.
Naghmouchi, Issam
2011.
On the measure of scrambled sets of tree maps with zero topological entropy.
Journal of Difference Equations and Applications,
Vol. 17,
Issue. 12,
p.
1715.
Cánovas, Jose S.
and
Daghar, Aymen
2023.
Topological sequence entropy and topological dynamics of tree maps.
Journal of Mathematical Analysis and Applications,
Vol. 525,
Issue. 1,
p.
127133.


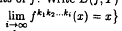 and g =
and g = 