Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T02:29:17.140Z Has data issue: false hasContentIssue false
  • English
  • Français

DOMINATION BY POSITIVE WEAK$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES

Part of: Special classes of linear operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  05 June 2014

JIN XI CHEN ,
ZI LI CHEN  and
GUO XING JI
JIN XI CHEN*
Affiliation:
Department of Mathematics, Southwest Jiaotong University, Chengdu 610031, PR China email [email protected]
ZI LI CHEN
Affiliation:
Department of Mathematics, Southwest Jiaotong University, Chengdu 610031, PR China email [email protected]
GUO XING JI
Affiliation:
College of Mathematics and Information Science, Shaanxi Normal University, Xi’an 710062, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, H’michane et al. [‘On the class of limited operators’, Acta Math. Sci. (submitted)] introduced the class of weak$^*$ Dunford–Pettis operators on Banach spaces, that is, operators which send weakly compact sets onto limited sets. In this paper, the domination problem for weak$^*$ Dunford–Pettis operators is considered. Let 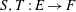$S, T:E\to F$ be two positive operators between Banach lattices 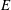$E$ and 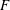$F$ such that 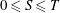$0\leq S\leq T$. We show that if 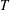$T$ is a weak$^{*}$ Dunford–Pettis operator and 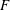$F$ is $\sigma $-Dedekind complete, then 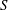$S$ itself is weak$^*$ Dunford–Pettis.

Keywords

limited setdomination propertyweak∗ Dunford–Pettis operatorpositive operatorBanach lattice

MSC classification

Secondary: 46B42: Banach lattices 47B65: Positive operators and order-bounded operators
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 311 - 318
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Aliprantis, C. D. and Burkinshaw, O., ‘Dunford–Pettis operators on Banach lattices’, Trans. Amer. Math. Soc. 274 (1982), 227–238.Google Scholar
Aliprantis, C. D. and Burkinshaw, O., Positive Operators (reprint of the 1985 original) (Springer, Dordrecht, 2006).Google Scholar
Andrews, K. T., ‘Dunford–Pettis sets in the space of Bochner integrable functions’, Math. Ann. 241 (1979), 35–41.Google Scholar
Borwein, J., Fabian, M. and Vanderwerff, J., ‘Characterizations of Banach spaces via convex and other locally Lipschitz functions’, Acta Math. Vietnam. 22 (1997), 53–69.Google Scholar
Bourgain, J. and Diestel, J., ‘Limited operators and strict cosingularity’, Math. Nachr. 119 (1984), 55–58.Google Scholar
Buhvalov, A. V., ‘Locally convex spaces that are generated by weakly compact sets (in Russian)’, Vestnik Leningrad Univ. No. 7 Mat. Meh. Astronom. 2 (1973), 11–17.Google Scholar
Burkinshaw, O., ‘Weak compactness in the order dual of a vector lattice’, Trans. Amer. Math. Soc. 187 (1974), 183–201.Google Scholar
Carrión, H., Galindo, P. and Lourenço, M. L., ‘A stronger Dunford–Pettis property’, Studia Math. 184 (2008), 205–216.CrossRefGoogle Scholar
Chen, J. X., Chen , Z. L. and Ji, G. X., ‘Almost limited sets in Banach lattices’, J. Math. Anal. Appl. 412 (2014), 547–553.Google Scholar
El Kaddouri, A., H’michane, J., Bouras, K. and Moussa, M., ‘On the class of weak∗ Dunford–Pettis operators’, Rend. Circ. Mat. Palermo (2) 62 (2013), 261–265.Google Scholar
H’michane, J., El Kaddouri, A., Bouras, K. and Moussa, M., ‘On the class of limited operators’, Acta Math. Sci., to appear, arXiv:1403.0136.Google Scholar
Kalton, N. J. and Saab, P., ‘Ideal properties of regular operators between Banach lattices’, Illinois J. Math. 29 (1985), 382–400.CrossRefGoogle Scholar
Meyer-Nieberg, P., Banach Lattices (Universitext) (Springer, Berlin, 1991).CrossRefGoogle Scholar
Wickstead, A. W., ‘Converses for the Dodds–Fremlin and Kalton–Saab theorems’, Math. Proc. Cambridge Philos. Soc. 120 (1996), 175–179.Google Scholar