Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Amano, Kazuo
1988.
The dirichlet problem for degenerate elliptic 2-dimensional monge-ampère equation: corrigendum.
Bulletin of the Australian Mathematical Society,
Vol. 38,
Issue. 3,
p.
479.
Kallel-Jallouli, Saoussen
2004.
The Dirichlet Problem for Degenerate Elliptic Darboux Equation.
Communications in Partial Differential Equations,
Vol. 29,
Issue. 7-8,
p.
1097.


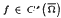 ,
, 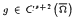 , find a solution
, find a solution 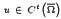 ,
, 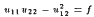 in Ω and
in Ω and 