Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:06:26.772Z Has data issue: false hasContentIssue false
  • English
  • Français

CONVERGENCE OF SOLUTIONS OF TIME-VARYING LINEAR SYSTEMS WITH INTEGRABLE FORCING TERM

Part of: Stability theory

Published online by Cambridge University Press:  01 December 2008

JITSURO SUGIE
JITSURO SUGIE*
Affiliation:
Department of Mathematics and Computer Science, Shimane University, Matsue 690-8504, Japan (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

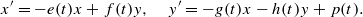The following system is considered in this paper: The primary goal is to establish conditions on time-varying coefficients e(t), f(t), g(t) and h(t) and a forcing term p(t) for all solutions to converge to the origin (0,0) as 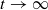. Here, the zero solution of the corresponding homogeneous linear system is assumed to be neither uniformly stable nor uniformly attractive. Sufficient conditions are given for asymptotic stability of the zero solution of the nonlinear perturbed system 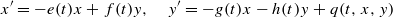under the assumption that q(t,0,0)=0.

Keywords

nonhomogeneous linear systemsweakly integrally positiveperturbation problems

MSC classification

Secondary: 34D05: Asymptotic properties 34D10: Perturbations 34D20: Stability
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 78 , Issue 3 , December 2008 , pp. 445 - 462
Copyright
Copyright © 2009 Australian Mathematical Society

References

[1]Coppel, W. A., Stability and Asymptotic Behavior of Differential Equations (Heath, Boston, MA, 1965).Google Scholar
[2]Halanay, A., Differential Equations: Stability, Oscillations, Time Lags (Academic Press, New York, 1966).Google Scholar
[3]Hale, J. K., Ordinary Differential Equations (Wiley-Interscience, New York, 1969). (Revised, Krieger, Malabar, 1980).Google Scholar
[4]Hatvani, L., ‘A generalization of the Barbashin-Krasovskij theorems to the partial stability in nonautonomous systems’, in: Qualitative Theory of Differential Equations I, II, Colloquia Mathematica Societatis János Bolyai, 30 (ed. M. Farkas) (North-Holland, Amsterdam, 1981), pp. 381–409.Google Scholar
[5]Hatvani, L., ‘On the uniform attractivity of solutions of ordinary differential equations by two Lyapunov functions’, Proc. Japan Acad. 67 (1991), 162–167.Google Scholar
[6]Hatvani, L., ‘On the asymptotic stability for a two-dimensional linear nonautonomous differential system’, Nonlinear Anal. 25 (1995), 991–1002.Google Scholar
[7]LaSalle, J. P. and Lefschetz, S., Stability by Liapunov’s Direct Method with Applications, Mathematics in Science and Engineering, 4 (Academic Press, New York, 1961).Google Scholar
[8]Merkin, D. R., Introduction to the Theory of Stability, Texts in Applied Mathematics, 24 (Springer, New York, 1997).Google Scholar
[9]Rouche, N., Habets, P. and Laloy, M., Stability Theory by Liapunov’s Direct Method, Applied Mathematical Sciences, 22 (Springer, New York, 1977).Google Scholar
[10]Strauss, A. and Yorke, J. A., ‘Perturbing uniformly stable linear systems with and without attraction’, SIAM J. Appl. Math. 17 (1969), 725–738.Google Scholar
[11]Sugie, J., ‘Influence of anti-diagonals on the asymptotic stability for linear differential systems’, accepted for Monatsh. Math. at press.Google Scholar
[12]Yoshizawa, T., Stability Theory by Liapunov’s Second Method, Publications of the Mathematical Society of Japan, 9 (Mathematical Society of Japan, Tokyo, 1966).Google Scholar