Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-08T09:02:58.471Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence criteria for Fourier series

Published online by Cambridge University Press:  17 April 2009

V. Venu Gopal Rao
V. Venu Gopal Rao
Affiliation:
Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The following convergence criterion of Fourier series is due to M. Izumi, S. Izumi and the author:

THEOREM. Let Δ ≥ 1. If

(i) 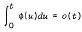, and

(ii) as t → 0

for an a, 0 < a < 1 and for a δ, 0 < δ < π, then the Fourier series of φ(t) is convergent at the origin.

The object of this paper is to generalize the above theorem in the Hardy-Littlewood direction.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 4 , Issue 2 , April 1971 , pp. 259 - 262
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Hardy, G.H. and Littlewood, J.E., “Notes on the theory of series (VII): On Young's convergence criterion for Fourier series”, Proc. London Math. Soc. (2) 28 (1928), 301–311.CrossRefGoogle Scholar
[2]Izumi, Masako, Izumi, Shin-ichi and Gopal Rao, V.V., “On the convergence criteria of Fourier series”, Proc. Japan Acad. (to appear).Google Scholar
[3]Pollard, S., “On the criteria for the convergence of a Fourier series”, J. London Math. Soc. 2 (1927), 255–262.CrossRefGoogle Scholar
[4]Sunouchi, Gen-ichirô, “Notes on Fourier analysis. XLVI. A convergence criterion for Fourier series”, Tôhoku Math. J. (2) 3 (1951), 216–219.Google Scholar