No CrossRef data available.
Article contents
A characterization of weak peak sets for function algebras
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let A ⊂ C(S) be a function algebra. In this paper we prove that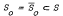 
is a weak peak set for A if and only if for any open neighbourhood U of S0 there is an f in A such that ∥f∥ ≤ 2, |f(x) − l| ≤ 1/3 on S0 and |f(x)| ≤ 1/3 on S\U.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1984
References
[1]Badé, W. and Curtis, P. Jr, “Embedding theorems for commutative Banach algebras”, Pacific J. Math. 18 (1966), 391–409.CrossRefGoogle Scholar
[2]Jarosz, K., “Metric and algebraic perturbations of function algebras”, Proc. Edinburgh Math. Soc. 26 (1983), 383–391.CrossRefGoogle Scholar
[3]Johnson, B.E., “Perturbations of Banach algebras”. Proc. London Math. Soc. (3) 34 (1977), 439–458.CrossRefGoogle Scholar
[4]Larsen, R., Banach algebras (Pure and Applied Mathematics #24, Marcel Dekker, Inc., New York, 1973).Google Scholar
[5]Rochberg, R., “Deformation of uniform algebras”, Proc. London Math. Soc. (3) 39 (1979), 93–118.CrossRefGoogle Scholar
You have
Access