Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T01:54:05.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Cauchy representation of distributions and applications to probability

Published online by Cambridge University Press:  17 April 2009

M. Aslam Chaudhry
M. Aslam Chaudhry
Affiliation:
Department of Mathematical Sciences KFUPM, Dhahran, Saudi Arabia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Cauchy representation is not valid for every Schwartz distribution f ∈ (D(R))′ because (t – x)−l ∉ D(R). Since for all z ∈ {z: Im z ≠ 0} the kernel (t – z)−l belongs to 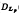(R) (1 > p > ∞), the Cauchy representation of the distributions in (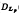(R))′ seems possible.

In this paper, we prove this fact. It is also proved that every probability density defines a generalised function on the space 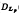(R)(1 < p < ∞), of test functions. Applications of these results in probability theory are discussed.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 42 , Issue 1 , August 1990 , pp. 125 - 131
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Bremermann, H.J., Distributions, Complex Variables and Fourier Transforms (Addison Wesley, 1965).Google Scholar
[2]Friedman, A., Generalized Functions and Partial Differential Equations (Prentice Hall, Englewood Cliffs, N.J., 1963).CrossRefGoogle Scholar
[3]Mitrovic, D., ‘A distributional representation of analytic functions’, Math. Balkanica 2 (1972), 161–164.Google Scholar
[4]Pandey, J.N. and Chaudhry, M.A., ‘Hilbert transform of generalized functions and applications’, Canad. J. Math. XXXV, No.3 (1983), 478–495.CrossRefGoogle Scholar
[5]Schwartz, L., Theories des Distributions, Vol. 1, II (Herman, Paris, 1957, 1959).Google Scholar
[6]Zemanian, A.H., Generalized Integral Transformations (Interscience Publishers, New York, 1968).Google Scholar