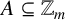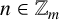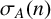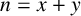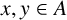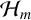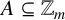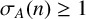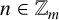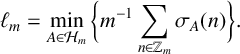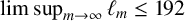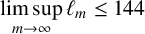1 Introduction
Let
$\mathbb {N}$
be the set of natural numbers and A a subset of
$\mathbb {N}$
. A remarkable conjecture of Erdős and Turán [Reference Erdős and Turán6] states that if all sufficiently large numbers n can be written as the sum of two elements of A, then the number of representations of n as the sum of two elements of A cannot be bounded. Progress on this conjecture was made by Grekos et al. [Reference Grekos, Haddad, Helou and Pihko8], who proved that the number of representations cannot be bounded by
$5$
, later improved to
$7$
by Borwein et al. [Reference Borwein, Choi and Chu1]. For more on the Erdős–Turán conjecture, see the books of Halberstam and Roth [Reference Halberstam and Roth10] and Tao and Vu [Reference Tao and Van Vu17].
A set A is called an asymptotic basis of natural numbers if all sufficiently large numbers n can be written as the sum of two elements of A. Motivated by Erdős’ question, Ruzsa [Reference Ruzsa12] constructed an asymptotic basis A of natural numbers which has a bounded square mean value. Ruzsa also considered a variant on the Erdős–Turán conjecture. Let
$\mathbb {Z}_m$
be the set of residue classes mod m and A a subset of
$\mathbb {Z}_m$
. For any
$n\in \mathbb {Z}_m$
, let
$$ \begin{align*} \sigma_A(n)=\#\{(x,y):n=x+y,~x,y\in \mathbb{Z}_m\}. \end{align*} $$
The Ruzsa number
$R_m$
is defined to be the least positive integer r so that there exists a set
$A\subseteq \mathbb {Z}_m$
with
$ 1\le \sigma _A(n)\le r \mbox { for all } n\in \mathbb {Z}_m. $
In his argument, Ruzsa proved that there is an absolute constant C such that
$R_m\le C$
for all positive integers m. Employing Ruzsa’s ideas, Tang and Chen [Reference Tang and Chen15] proved that
$R_m\le 768$
for all sufficiently large m. Later, in [Reference Tang and Chen16], they obtained
$R_m\le 5120$
for all positive integers m. In [Reference Chen2], Chen proved that
$R_m\le 288$
for all positive integers m, and this was recently improved to
$R_m\le 192$
by Ding and Zhao [Reference Ding and Zhao5]. However, Sándor and Yang [Reference Sándor and Yang13] showed that
$R_m\ge 6$
for all
$m\ge 36$
.
Ding and Zhao [Reference Ding and Zhao5] provided an average version of Ruzsa’s number. Precisely, let
$\mathcal {H}_m$
be the set of subsets
$A\subseteq \mathbb {Z}_m$
such that
$\sigma _A(n)\geq 1$
for all
$n\in \mathbb {Z}_m$
. Ding and Zhao defined the minimal mean value as
$$ \begin{align*} \ell_m=\min\limits_{A\in \mathcal{H}_m}\bigg\lbrace m^{-1}\sum_{n\in \mathbb{Z}_m}\sigma_A(n)\bigg\rbrace. \end{align*} $$
As they pointed out, their result on
$R_m\le 192$
clearly implies
$$ \begin{align} \limsup_{m\rightarrow\infty}\ell_m\le 192. \end{align} $$
Ding and Zhao [Reference Ding and Zhao5, Section 3] thought that ‘any improvement of the bound (1.1) would be of interest’. In this note, we shall make some progress on this problem.
Theorem 1.1. We have
$$ \begin{align*} \limsup\limits_{m\rightarrow\infty}\ell_m\leq 144. \end{align*} $$
Parallel to the additive bases of
$\mathbb {Z}_m$
, one naturally considers the corresponding results on subtractive bases of
$\mathbb {Z}_m$
. Let A be a subset of
$\mathbb {Z}_m$
. For any
$n\in \mathbb {Z}_m$
, let
$$ \begin{align*} \delta_A(n)=\#\{(x,y):n=x-y,~x,y\in \mathbb{Z}_m\}. \end{align*} $$
In [Reference Chen and Sun3], Chen and Sun proved that for any positive integer m, there exists a subset A of
$\mathbb {Z}_m$
so that
$\delta _A(n)\ge 1$
for any
$n\in \mathbb {Z}_m$
and
$\delta _A(n)\le 7$
for all
$n\in \mathbb {Z}_m$
with three exceptions. Their result was recently improved by Zhang [Reference Zhang18] who showed that
$\delta _A(n)\le 7$
could be refined to
$\delta _A(n)\le 5$
, again with three exceptions. The exceptions cannot be removed by their method. Motivated by the minimal mean value defined by Ding and Zhao, we consider a parallel quantity
$$ \begin{align*} g_m:=\min\limits_{A\in \mathcal{K}_m}\bigg\lbrace m^{-1}\sum_{n\in \mathbb{Z}_m}\delta_A(n)\bigg\rbrace, \end{align*} $$
where
$\mathcal {K}_m$
is the set of subsets
$A\subseteq \mathbb {Z}_m$
such that
$\delta _A(n)\geq 1$
for all
$n\in \mathbb {Z}_m$
. Obviously, Zhang’s bound implies that
$$ \begin{align*} \limsup\limits_{m\rightarrow\infty}g_m\leq 5 \end{align*} $$
since the total sums of
$\delta _A(n)$
for the three exceptions contribute only
$O(\sqrt {m})$
. Our second main result gives a small improvement on this bound.
Theorem 1.2. We have
$$ \begin{align*} \limsup\limits_{m\rightarrow\infty}g_m\leq 2. \end{align*} $$
There is an old conjecture known as the prime power conjecture (see, for example, [Reference Evans and Mann7, Reference Guy9, Reference Hall11]) which states that if A is a subset of
$\mathbb {Z}_m$
with
$\delta _A(n)=1$
for any nonzero
$ n\in \mathbb {Z}_m$
, then
$m=p^{2\alpha }+p^\alpha +1$
, where
$p^\alpha $
is a prime power. The reverse direction was proved by Singer [Reference Singer14] as early as 1938.
As mentioned by Ding and Zhao [Reference Ding and Zhao5], it is clear that
$\liminf _{m\rightarrow \infty }\ell _m\ge 2$
from [Reference Sándor and Yang13, Lemma 2.2]. They conjectured that
$\liminf _{m\rightarrow \infty }\ell _m\ge 3$
[Reference Ding and Zhao5, Conjecture 3.3]. Based on the results of Singer and Theorem 1.2, it seems reasonable to conjecture that
$$ \begin{align*} \lim\limits_{m\rightarrow\infty}g_m=1. \end{align*} $$
If true, these conjectures reflect rather different features between additive bases and subtractive bases.
2 Proof of Theorem 1.1
For any integer k, let
$$ \begin{align*} Q_k=\{(u,ku^2):u\in \mathbb{Z}_{p}\}\subset \mathbb{Z}_{p}^2. \end{align*} $$
We will make use of the following lemmas.
Lemma 2.1 (Chen [Reference Chen2, Lemma 2]).
Let p be an odd prime and m a quadratic nonresidue of p with
$m+1\not \equiv 0 \pmod {p}, 3m+1\not \equiv 0\pmod {p}$
and
$m+3\not \equiv 0 \pmod {p}$
. Put
$$ \begin{align*} B=Q_{m+1}\cup Q_{m(m+1)}\cup Q_{2m}. \end{align*} $$
Then, for any
$(c,d)\in \mathbb {Z}_{p}^2$
, we have
$1\le \sigma _B(c,d)\le 16$
, where
$\sigma _B(c,d)$
is the number of solutions of the equation
$(c,d)=x+y,~x,y\in B$
.
Lemma 2.2 (Prime number theorem; see, for example, [Reference Davenport4]).
Let
$\pi (x)$
be the number of primes p not exceeding x. Then,
$$ \begin{align*} \pi(x)\sim x/\!\log x \quad \text{as~} x\rightarrow\infty. \end{align*} $$
Lemma 2.3. Let m be a positive integer and A a subset of
$\mathbb {Z}_m$
. Then,
$$ \begin{align*} \sum_{n\in \mathbb{Z}_m}\sigma_A(n)=|A|^2, \end{align*} $$
where
$|A|$
denotes the number of elements of A.
Proof. Clearly,
$$ \begin{align*} \sum\limits_{n\in \mathbb{Z}_m}\sigma_A(n)=\sum\limits_{n\in\mathbb{Z}_m}\sum\limits_{\substack{a_1+a_2=n\\a_1,a_2\in A}}1=\sum\limits_{\substack{a_1,a_2\in A\\a_1+a_2\in \mathbb{Z}_m}}1=\sum\limits_{a_1,a_2\in A}1=|A|^{2}. \end{align*} $$
This completes the proof of Lemma 2.3.
Lemma 2.4. Let p be a prime greater than
$11$
. Then there is a subset
$A\subset \mathbb {Z}_{2p^2}$
with
$|A|\le 12p$
so that
$\sigma _A(n)\ge 1$
for any
$n\in \mathbb {Z}_{2p^2}$
.
Proof. Let p be a prime greater than
$11$
. Then there are at least
$(p-1)/2>5$
quadratic nonresidues mod p, which means that there is some quadratic nonresidue m so that
$$ \begin{align*} m+1\not\equiv 0 \pmod{p}, \quad 3m+1\not\equiv 0\pmod{p} \quad \text{and} \quad m+3\not\equiv 0 \pmod{p}. \end{align*} $$
Let
$B=Q_{m+1}\cup Q_{m(m+1)}\cup Q_{2m}$
,
$A_1=\lbrace u+2pv:(u,v)\in B\rbrace $
and
$A=A_1\cup (A_1+p)$
, where
$A_1+p:=\{a_1+p:a_1\in A_1\}$
. Obviously, A can be viewed as a subset of
$\mathbb {Z}_{2p^2}$
.
We first show that
$\sigma _A(n)\ge 1$
for any
$n\in \mathbb {Z}_{2p^2}$
, that is,
$A\in \mathcal {H}_{2p^2}$
(by the definition of
$\mathcal {H}_{m}$
). We follow the proof of Chen [Reference Chen2, Theorem 1]. For any
$(u,v)\in B$
, we have
$0\le u,v\le p-1$
. Let n be an element of
$\mathbb {Z}_{2p^2}$
with
$0\le n\le 2p^2-1$
. Then, we can assume that
$$ \begin{align*} n=c+2pd \end{align*} $$
with
$p\le c\le 3p-1$
and
$-1\le d\le p-1$
. By Lemma 2.1, there are
$(u_1,v_1),(u_2,v_2)\in B$
so that
$$ \begin{align*} (c,d)=(u_1,v_1)+(u_2,v_2) \pmod{p}, \end{align*} $$
or in other words,
$$ \begin{align*} c\equiv u_1+u_2 \pmod{p} \quad \text{and} \quad d\equiv v_1+v_2 \pmod{p}. \end{align*} $$
Suppose that
$$ \begin{align*} c=u_1+u_2+ps \quad \text{and} \quad d=v_1+v_2+ph, \end{align*} $$
with
$s,h\in \mathbb {Z}$
. Then,
$s=0$
or
$1$
or
$2$
since
$0\le u_1+u_2\le 2p-2$
and
$p\le c\le 3p-1$
. Hence,
$$ \begin{align*} n&=c+2pd\\ &= u_1+2pv_1+u_2+2pv_2+ps+2p^2h \\ &\equiv u_1+2pv_1+u_2+2pv_2+ps \pmod{2p^2}. \end{align*} $$
If
$s=0$
, then in
$\mathbb {Z}_{2p^2}$
,
$$ \begin{align*} n= (u_1+2pv_1)+(u_2+2pv_2)\in A_1+A_1\subset A+A. \end{align*} $$
If
$s=1$
, then in
$\mathbb {Z}_{2p^2}$
,
$$ \begin{align*} n= (u_1+2pv_1+p)+(u_2+2pv_2)\in (A_1+p)+A_1\subset A+A. \end{align*} $$
If
$s=2$
, then in
$\mathbb {Z}_{2p^2}$
,
$$ \begin{align*} n= (u_1+2pv_1+p)+(u_2+2pv_2+p)\in (A_1+p)+(A_1+p)\subset A+A. \end{align*} $$
Hence, in all cases,
$\sigma _A(n)\ge 1$
for
$n\in \mathbb {Z}_{2p^2}$
.
It can be easily seen that
$|A_1|\le 2|B|$
from the construction. Therefore, for the set A constructed above,
$$ \begin{align*} |A|\le |A_1|+|A_1+p|=2|A_1|\le 2\times 2|B|=4|B| \end{align*} $$
and
$$ \begin{align*} |B|\leqslant|Q_{m+1}|+|Q_{m(m+1)}|+|Q_{2m}|=3p, \end{align*} $$
from which it follows that
$$ \begin{align*} |A|\le 12p. \end{align*} $$
This completes the proof of Lemma 2.4.
The final lemma gives a relation between the bases of
$\mathbb {Z}_{m_1}$
and
$\mathbb {Z}_{m_2}$
with certain constraints.
Lemma 2.5. Let
$\varepsilon>0$
be an arbitrarily small number. Let
$m_1$
and
$m_2$
be two positive integers with
$(2-\varepsilon )m_1<m_2<2m_1$
. If A is a subset of
$\mathbb {Z}_{m_1}$
with
$\sigma _A(n)\ge 1$
for any
$n\in \mathbb {Z}_{m_1}$
, then there is a subset B of
$\mathbb {Z}_{m_2}$
with
$|B|\le 2|A|$
such that
$\sigma _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m_2}$
.
Proof. Suppose that
$m_2=m_1+r$
, so that
$(1-\varepsilon )m_1<r< m_1$
. Let
$$ \begin{align*} B=A\cup \{a+r:a\in A\}. \end{align*} $$
Then,
$|B|\le 2|A|$
. It remains to prove
$\sigma _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m_2}$
.
Without loss of generality, we may assume
$0\le a\le m_1-1$
for any
$a\in A$
. For
$0\le n\le m_1-1$
, there are two integers
$a_1,a_2\in A$
so that
$ n\equiv a_1+a_2\pmod {m_1}. $
Since
$0\le a_1+a_2\le 2m_1-2$
, it follows that
$$ \begin{align*} n=a_1+a_2 \quad \text{or} \quad n=a_1+a_2-m_1. \end{align*} $$
If
$n=a_1+a_2$
, then clearly
$n\equiv a_1+a_2\pmod {m_2}$
. If
$n=a_1+a_2-m_1$
, then
$$ \begin{align*} n+m_2=n+m_1+r=a_1+(a_2+r), \end{align*} $$
which means that
$n\equiv a_1+(a_2+r)\pmod {m_2}$
. In both cases,
$\sigma _B(n)\ge 1$
for any n with
$0\le n\le m_1-1$
. We are left to consider the case
$m_1\le n\le m_2-1$
. In this range,
$$ \begin{align*} 0<n-r\le m_2-1-r= m_1-1. \end{align*} $$
Thus, there are two elements
$\widetilde {a_1},\widetilde {a_2}$
of A so that
$$ \begin{align*} n-r\equiv \widetilde{a_1}+\widetilde{a_2}\pmod{m_1}. \end{align*} $$
Again, by the constraint
$0\le \widetilde {a_1}+\widetilde {a_2}\le 2m_1-2$
,
$$ \begin{align*} n-r=\widetilde{a_1}+\widetilde{a_2} \quad \text{or} \quad n-r=\widetilde{a_1}+\widetilde{a_2}-m_1. \end{align*} $$
If
$n-r=\widetilde {a_1}+\widetilde {a_2}$
, then we clearly have
$n-r\equiv \widetilde {a_1}+\widetilde {a_2}\pmod {m_2}$
. Otherwise, we have
$n-r=\widetilde {a_1}+\widetilde {a_2}-m_1$
. So, it can now be deduced that
$$ \begin{align*} n+m_2=\widetilde{a_1}+r+\widetilde{a_2}+r, \end{align*} $$
which is equivalent to
$n\equiv (\widetilde {a_1}+r)+(\widetilde {a_2}+r)\pmod {m_2}$
.
Proof of Theorem 1.1.
Let
$\varepsilon>0$
be an arbitrarily small given number. Then, by Lemma 2.2, there is some prime p so that
$$ \begin{align} \sqrt{\frac{m}{4}}<p<\sqrt{\frac{m}{2(2-\varepsilon)}}, \end{align} $$
provided that m is sufficiently large (in terms of
$\varepsilon $
). By Lemma 2.4, there is a subset
$A\subset \mathbb {Z}_{2p^2}$
with
$|A|\le 12p$
so that
$\sigma _{A}(n)\ge 1$
for any
$n\in \mathbb {Z}_{2p^2}$
. From (2.1),
$$ \begin{align} (2-\varepsilon)2p^2<m<2\times2p^2. \end{align} $$
Thus, by Lemma 2.5, there is a subset B of
$\mathbb {Z}_{m}$
with
$$ \begin{align} |B|\le 2|A|\le 24p \end{align} $$
such that
$\sigma _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m}$
. Hence, by Lemma 2.3,
$$ \begin{align*} \ell_m=\min\limits_{\widetilde{A}\in \mathcal{H}_m}\bigg\lbrace m^{-1}\sum_{n\in \mathbb{Z}_m}\sigma_{\widetilde{A}}(n)\bigg\rbrace\le m^{-1}\sum_{n\in \mathbb{Z}_m}\sigma_{B}(n)=\frac{|B|^2}{m}. \end{align*} $$
$$ \begin{align*} \frac{|B|^2}{m}\le \frac{(24p)^2}{(2-\varepsilon)2p^2}=144\times\frac{2}{2-\varepsilon}. \end{align*} $$
Hence, it follows that
$$ \begin{align*} \limsup_{m\rightarrow\infty}\ell_m\le 144\times\frac{2}{2-\varepsilon} \end{align*} $$
for any
$\varepsilon>0$
, which clearly means that
$$ \begin{align*} \limsup_{m\rightarrow\infty}\ell_m\le 144. \end{align*} $$
This completes the proof of Theorem 1.1.
3 Proof of Theorem 1.2
The proof of Theorem 1.2 is based on the following remarkable result of Singer.
Lemma 3.1 (Singer [Reference Singer14]).
Let p be a prime. Then, there exists a subset A of
$\mathbb {Z}_{p^{2}+p+1}$
so that
$\delta _A(n)=1$
for any
$n\in \mathbb {Z}_{p^{2}+p+1}$
with
$n\neq \overline {0}$
.
The next lemma is a variant of Lemma 2.3.
Lemma 3.2. Let m be a positive integer and A a subset of
$\mathbb {Z}_m$
. Then,
$$ \begin{align*} \sum_{n\in \mathbb{Z}_m}\delta_A(n)=|A|^2, \end{align*} $$
where
$|A|$
denotes the number of elements of A.
Proof. It is clear that
$$ \begin{align*} \sum\limits_{n\in \mathbb{Z}_m}\delta_A(n)=\sum\limits_{n\in\mathbb{Z}_m}\sum\limits_{\substack{a_1-a_2=n\\a_1,a_2\in A}}1=\sum\limits_{\substack{a_1,a_2\in A\\a_1-a_2\in \mathbb{Z}_m}}1=\sum\limits_{a_1,a_2\in A}1=|A|^{2}. \end{align*} $$
This completes the proof of Lemma 3.2.
We need another auxiliary lemma.
Lemma 3.3. Let
$\varepsilon>0$
be an arbitrarily small number. Let m be a positive integer and p a prime number with
$$ \begin{align*} (2-\varepsilon)(p^{2}+p+1)<m<2(p^{2}+p+1). \end{align*} $$
If A is a subset of
$\mathbb {Z}_{p^{2}+p+1}$
with
$\delta _A(n)\ge 1$
for any
$n\in \mathbb {Z}_{p^{2}+p+1}$
, then there is a subset B of
$\mathbb {Z}_{m}$
with
$|B|\le 2|A|$
such that
$\delta _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m}$
.
Proof. Suppose that
$m{\kern-1pt}={\kern-1pt}(p^2{\kern-1pt}+{\kern-1pt}p{\kern-1pt}+{\kern-1pt}1){\kern-1pt}+{\kern-1pt}r$
. Then,
$(1-\varepsilon )(p^2{\kern-1pt}+{\kern-1pt}p{\kern-1pt}+{\kern-1pt}1){\kern-1pt}<{\kern-1pt}r{\kern-1pt}<{\kern-1pt} (p^2{\kern-1pt}+{\kern-1pt} p{\kern-1pt}+{\kern-1pt}1)$
. Let
$$ \begin{align*} B=A\cup \{a+r:a\in A\}. \end{align*} $$
Then,
$|B|\le 2|A|$
. It remains to prove
$\delta _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m}$
.
Without loss of generality, we can assume
$0\le a\le p^2+p$
for any
$a\in A$
. For
$0\le n\le p^2+p$
, there are two integers
$a_1,a_2\in A$
so that
$$ \begin{align*} n\equiv a_1-a_2\pmod{p^2+p+1}, \end{align*} $$
which means that
$$ \begin{align*} n= a_1-a_2 \quad \text{or} \quad n=a_1-a_2+(p^2+p+1) \end{align*} $$
since
$-p^2-p\le a_1-a_2\le p^2+p$
. If
$n=a_1-a_2$
, then we clearly have
$n\equiv a_1-a_2 \pmod {m}$
. If
$n=a_1-a_2+(p^2+p+1)$
, then
$$ \begin{align*} n-m=n-(p^2+p+1)-r=a_1-(a_2+r), \end{align*} $$
from which it can be deduced that
$n\equiv a_1-(a_2+r)\pmod {m}$
. In both cases, we have
$\delta _B(n)\ge 1$
for any n with
$0\le n\le p^2+p$
. We are left to consider the case
$p^2+p+1\le n\le m-1$
. In this case,
$$ \begin{align*} 0<n-r\le m-1-r=p^2+p. \end{align*} $$
Thus, there are two elements
$\widetilde {a_1},\widetilde {a_2}$
of A so that
$$ \begin{align*} n-r\equiv \widetilde{a_1}-\widetilde{a_2}\pmod{m}. \end{align*} $$
Again, by the constraint
$-p^2-p\le \widetilde {a_1}-\widetilde {a_2}\le p^2+p$
, we have
$$ \begin{align*} n-r=\widetilde{a_1}-\widetilde{a_2} \quad \text{or} \quad n-r=\widetilde{a_1}-\widetilde{a_2}+(p^2+p+1). \end{align*} $$
If
$n-r=\widetilde {a_1}-\widetilde {a_2}$
, then we clearly have
$n-r\equiv \widetilde {a_1}-\widetilde {a_2}\pmod {m}$
. Otherwise, we have
$n-r=\widetilde {a_1}-\widetilde {a_2}+(p^2+p+1)$
, from which it clearly follows that
$$ \begin{align*} n-m=\widetilde{a_1}-\widetilde{a_2}. \end{align*} $$
So we also deduce
$n\equiv \widetilde {a_1}-\widetilde {a_2}\pmod {m}$
.
We now turn to the proof of Theorem 1.2.
Proof of Theorem 1.2.
Let
$\varepsilon>0$
be an arbitrarily small given number. By Lemma 2.2, there is some prime p so that
$$ \begin{align*} \frac{\sqrt{2m-3}-1}{2}<p<\frac{\sqrt{\frac{4}{2-\varepsilon}m-3}-1}{2} \end{align*} $$
providing that m is sufficiently large (in terms of
$\varepsilon $
). Equivalently,
$$ \begin{align} (2-\varepsilon)(p^{2}+p+1)<m<2(p^{2}+p+1). \end{align} $$
By Lemma 3.1, there is a subset A of
$\mathbb {Z}_{p^{2}+p+1}$
so that
$\delta _A(n)=1$
for any
$n\in \mathbb {Z}_{p^{2}+p+1}$
with
$n\neq \overline {0}$
. Employing Lemma 3.2,
$$ \begin{align*} |A|^2=\sum\limits_{n\in \mathbb{Z}_{p^{2}+p+1}}\delta_A(n)=\sum\limits_{n\in \mathbb{Z}_{p^{2}+p+1},~n\neq \overline{0}}\delta_A(n)+\delta_A(0)=p^{2}+p+|A|, \end{align*} $$
from which it follows clearly that
$$ \begin{align*} |A|=p+1. \end{align*} $$
By Lemma 3.3 and (3.1), there is a subset B of
$\mathbb {Z}_{m}$
with
$$ \begin{align} |B|\le 2|A|\le 2(p+1) \end{align} $$
such that
$\delta _B(n)\ge 1$
for any
$n\in \mathbb {Z}_{m}$
. Thus, by the definition of
$g_m$
and Lemma 3.2 again,
$$ \begin{align*} g_m=\min\limits_{\widetilde{A}\in \mathcal{K}_m}\bigg\lbrace m^{-1}\sum_{n\in \mathbb{Z}_m}\delta_{\widetilde{A}}(n)\bigg\rbrace\le m^{-1}\sum_{n\in \mathbb{Z}_m}\delta_{B}(n)=\frac{|B|^2}{m}. \end{align*} $$
$$ \begin{align*} \frac{|B|^2}{m}\le \frac{4(p+1)^2}{(2-\varepsilon)(p^{2}+p+1)}\le \frac{4}{2-\varepsilon/2}, \end{align*} $$
provided that m (hence p) is sufficiently large (in terms of
$\varepsilon $
). Hence, we conclude that
$$ \begin{align*} \limsup_{m\rightarrow\infty}g_m\le \frac{4}{2-\varepsilon/2} \end{align*} $$
for any
$\varepsilon>0$
, which clearly means that
$$ \begin{align*} \limsup_{m\rightarrow\infty}g_m\le 2. \end{align*} $$
This completes the proof of Theorem 1.2.
Acknowledgement
The authors would like to thank Professor Yuchen Ding for his generous help and very helpful comments.
