Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-24T17:18:01.781Z Has data issue: false hasContentIssue false
  • English
  • Français

SUM-PRODUCT ESTIMATES FOR DIAGONAL MATRICES

Part of: Polynomials and matrices Sequences and sets

Published online by Cambridge University Press:  24 June 2020

AKSHAT MUDGAL Open the ORCID record for AKSHAT MUDGAL [Opens in a new window]
AKSHAT MUDGAL*
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067, USA School of Mathematics, University of Bristol, Fry Building, Woodland Road, Bristol, BS8 1UG, UK email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given 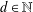$d\in \mathbb{N}$, we establish sum-product estimates for finite, nonempty subsets of 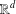$\mathbb{R}^{d}$. This is equivalent to a sum-product result for sets of diagonal matrices. In particular, let 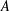$A$ be a finite, nonempty set of 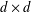$d\times d$ diagonal matrices with real entries. Then, for all 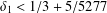$\unicode[STIX]{x1D6FF}_{1}<1/3+5/5277$,

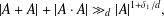$$\begin{eqnarray}|A+A|+|A\cdot A|\gg _{d}|A|^{1+\unicode[STIX]{x1D6FF}_{1}/d},\end{eqnarray}$$
which strengthens a result of Chang [‘Additive and multiplicative structure in matrix spaces’, Combin. Probab. Comput.16(2) (2007), 219–238] in this setting.

Keywords

arithmetic combinatoricssum-product estimates

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11C20: Matrices, determinants
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 28 - 37
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author’s work was supported in part by a studentship sponsored by a European Research Council Advanced Grant under the European Union’s Horizon 2020 research and innovation programme via grant agreement no. 695223.

References

Basit, A. and Lund, B., ‘An improved sum-product bound for quaternions’, SIAM J. Discrete Math. 33(2) (2019), 1044–1060.10.1137/18M1231468CrossRefGoogle Scholar
Bloom, T. and Jones, T., ‘A sum-product theorem in function fields’, Int. Math. Res. Not. IMRN 2014(19) (2014), 5249–5263.10.1093/imrn/rnt125CrossRefGoogle Scholar
Chang, M. C., ‘A sum-product estimate in algebraic division algebras’, Israel J. Math. 150 (2005), 369–380.CrossRefGoogle Scholar
Chang, M. C., ‘Additive and multiplicative structure in matrix spaces’, Combin. Probab. Comput. 16(2) (2007), 219–238.10.1017/S0963548306008145CrossRefGoogle Scholar
Erdős, P. and Szemerédi, E., ‘On sums and products of integers’, in: Studies in Pure Mathematics (Birkhäuser, Basel, 1983), 213–218.10.1007/978-3-0348-5438-2_19CrossRefGoogle Scholar
Granville, A. and Solymosi, J., ‘Sum-product formulae’, in: Recent Trends in Combinatorics, The IMA Volumes in Mathematics and its Applications, 159 (Springer, Cham, 2016), 419–451.10.1007/978-3-319-24298-9_18CrossRefGoogle Scholar
Konyagin, S. V. and Rudnev, M., ‘On new sum-product-type estimates’, SIAM J. Discrete Math. 27(2) (2013), 973–990.10.1137/120886418CrossRefGoogle Scholar
Shakan, G., ‘On higher energy decompositions and the sum-product phenomenon’, Math. Proc. Cambridge Philos. Soc. 167(3) (2019), 599–617.10.1017/S0305004118000506CrossRefGoogle Scholar
Solymosi, J., ‘On sum-sets and product-sets of complex numbers’, J. Théor. Nombres Bordeaux 17(3) (2005), 921–924.10.5802/jtnb.527CrossRefGoogle Scholar
Solymosi, J. and Tao, T., ‘An incidence theorem in higher dimensions’, Discrete Comput. Geom. 48(2) (2012), 255–280.10.1007/s00454-012-9420-xCrossRefGoogle Scholar
Solymosi, J. and Vu, V. H., ‘Sum-product estimates for well-conditioned matrices’, Bull. Lond. Math. Soc. 41(5) (2009), 817–822.10.1112/blms/bdp054CrossRefGoogle Scholar
Solymosi, J. and Wong, C., ‘An application of kissing number in sum-product estimates’, Acta Math. Hungar. 155(1) (2018), 47–60.CrossRefGoogle Scholar
Tao, T., ‘The sum-product phenomenon in arbitrary rings’, Contrib. Discrete Math. 4(2) (2009), 59–82.Google Scholar