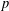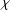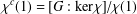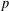Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ahanjideh, Neda
2021.
The one-prime hypothesis on the co-degrees of irreducible characters.
Communications in Algebra,
Vol. 49,
Issue. 9,
p.
4016.
Bahramian, Roya
and
Ahanjideh, Neda
2021.
p-parts of co-degrees of irreducible characters.
Comptes Rendus. Mathématique,
Vol. 359,
Issue. 1,
p.
79.
Ahanjideh, Neda
2022.
Co-degree Graphs and Order Elements.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 5,
p.
2653.
AHANJIDEH, NEDA
2022.
NONDIVISIBILITY AMONG IRREDUCIBLE CHARACTER CO-DEGREES.
Bulletin of the Australian Mathematical Society,
Vol. 105,
Issue. 1,
p.
68.
Ahanjideh, Neda
2023.
Finite groups admitting at most two irreducible characters having equal co-degrees.
Journal of Algebra and Its Applications,
Vol. 22,
Issue. 04,
Bahramian, Roya
Ahanjideh, Neda
and
Naghipour, Ali Reza
2023.
Groups with some cube-free irreducible character co-degrees.
Communications in Algebra,
Vol. 51,
Issue. 4,
p.
1772.
Bahramian, Roya
Ahanjideh, Neda
and
Naghipour, Ali Reza
2024.
The character co-degree sets and solvability.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 06,
Wang, Zhongbi
Qian, Guohua
Lv, Heng
and
Chen, Guiyun
2024.
On the average codegree of a finite group.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 05,
Gao, Li
Wang, Zhongbi
and
Chen, Guiyun
2024.
Finite groups with gcd(χ(1), χc
(1)) a prime.
Open Mathematics,
Vol. 22,
Issue. 1,