Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T15:20:22.386Z Has data issue: false hasContentIssue false
  • English
  • Français

ON UNRAMIFIED SOLVABLE EXTENSIONS OF SMALL NUMBER FIELDS

Part of: Algebraic number theory: global fields Field extensions

Published online by Cambridge University Press:  09 November 2020

JOACHIM KÖNIG Open the ORCID record for JOACHIM KÖNIG [Opens in a new window]
JOACHIM KÖNIG*
Affiliation:
Department of Mathematics Education, Korea National University of Education, Cheongju, South Korea
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate unramified extensions of number fields with prescribed solvable Galois group G and certain extra conditions. In particular, we are interested in the minimal degree of a number field K, Galois over 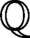$\mathbb {Q}$ , such that K possesses an unramified G-extension. We improve the best known bounds for the degree of such number fields K for certain classes of solvable groups, in particular for nilpotent groups.

Keywords

Galois theorynilpotent groupsolvable groupunramified extension

MSC classification

Primary: 11R32: Galois theory
Secondary: 12F12: Inverse Galois theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 3 , June 2021 , pp. 428 - 437
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baumslag, G., ‘Wreath products and $p$ -groups’, Math. Proc. Cambridge Philos. Soc. 55(3) (1959), 224–231.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
Hall, P., ‘A contribution to the theory of groups of prime power order’, Proc. Lond. Math. Soc. Ser. 2 36(1) (1934), 29–95.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen, Part I (Springer, Berlin, 1967).CrossRefGoogle Scholar
Kim, K.-S., ‘Construction of unramified extensions with a prescribed Galois group’, Osaka J. Math. 52 (2015), 1039–1050.Google Scholar
Kim, K.-S., ‘Construction of unramified extensions with a prescribed solvable Galois group’, Acta Arith. 190 (2019), 49–56.CrossRefGoogle Scholar
Kim, K.-S. and König, J., ‘On Galois extensions with prescribed decomposition groups’, J. Number Theory, to appear.Google Scholar
König, J., Neftin, D. and Sonn, J., ‘Unramified extensions over low degree number fields’, J. Number Theory 212 (2020), 72–87.CrossRefGoogle Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields (Springer, Berlin, 2000).Google Scholar
Nomura, A., ‘On the existence of unramified $p$ -extensions with prescribed Galois group’, Osaka J. Math. 47 (2010), 1159–1165.Google Scholar
Uchida, K., ‘Unramified extensions of quadratic number fields, II’, Tohoku Math. J. 22 (1970), 220–224.Google Scholar
Wood, M. M., ‘Nonabelian Cohen–Lenstra moments’, Duke Math. J. 168(3) (2019), 377–427.CrossRefGoogle Scholar
Yamamoto, Y., ‘On unramified Galois extensions of quadratic number fields’, Osaka J. Math. 7 (1970), 57–76.Google Scholar