Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T07:08:48.654Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE POSITION OF NODES OF PLANE CURVES

Part of: Cycles and subschemes Curves

Published online by Cambridge University Press:  01 June 2020

CÉSAR LOZANO HUERTA Open the ORCID record for CÉSAR LOZANO HUERTA [Opens in a new window]  and
TIM RYAN Open the ORCID record for TIM RYAN [Opens in a new window]
CÉSAR LOZANO HUERTA*
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, Oaxaca, Mexico email [email protected]
TIM RYAN
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, USA email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Severi variety 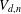$V_{d,n}$ of plane curves of a given degree 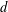$d$ and exactly $n$ nodes admits a map to the Hilbert scheme 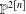$\mathbb{P}^{2[n]}$ of zero-dimensional subschemes of 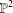$\mathbb{P}^{2}$ of degree $n$. This map assigns to every curve 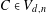$C\in V_{d,n}$ its nodes. For some $n$, we consider the image under this map of many known divisors of the Severi variety and its partial compactification. We compute the divisor classes of such images in 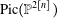$\text{Pic}(\mathbb{P}^{2[n]})$ and provide enumerative numbers of nodal curves. We also answer directly a question of Diaz–Harris [‘Geometry of the Severi variety’, Trans. Amer. Math. Soc.309 (1988), 1–34] about whether the canonical class of the Severi variety is effective.

Keywords

Hilbert scheme of pointsSeveri varietynodal plane curves

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14C22: Picard groups 14H50: Plane and space curves
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 62 - 68
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

During the preparation of this article the first named author was partly supported by the CONACYT grant CB-2015/253061; he is currently a CONACYT Research Fellow in Mathematics, project no. 1036.

References

Arbarello, E. and Cornalba, M., ‘Footnotes to a paper of Beniamino Segre’, Math. Ann. 256 (1981), 341–362.CrossRefGoogle Scholar
Boucksom, S., Demailly, J. P., Păun, M. and Peternell, T., ‘The pseudo-effective cone of a compact Kähler manifold and varieties of negative Kodaira dimension’, J. Algebraic Geom. 22(2) (2013), 201–248.CrossRefGoogle Scholar
Diaz, S. and Harris, J., ‘Geometry of the Severi variety’, Trans. Amer. Math. Soc. 309 (1988), 1–34.CrossRefGoogle Scholar
Diaz, S. and Harris, J., ‘Ideals associated to deformations of singular plane curves’, Trans. Amer. Math. Soc. 309 (1988), 433–468.CrossRefGoogle Scholar
Fulton, W., Intersection Theory (Springer, New York, 1998).10.1007/978-1-4612-1700-8CrossRefGoogle Scholar
Huizenga, J., ‘Effective divisors on the Hilbert scheme of points in the plane and interpolation for stable bundles’, J. Algebraic Geom. 25 (2016), 19–75.CrossRefGoogle Scholar
Lozano Huerta, C. and Ryan, T., ‘On the birational geometry of Hilbert schemes of points and Severi divisors’, Comm. Algebra (to appear), arXiv:1807.09881.Google Scholar
Sernesi, E., Deformations of Algebraic Schemes, Grundlehren der mathematischen Wissenschaften, 334 (Springer, Berlin–Heidelberg, 2006).Google Scholar
Treger, R., ‘Plane curves with nodes’, Canad. J. Math. 41(2) (1989), 193–212.CrossRefGoogle Scholar