No CrossRef data available.
Published online by Cambridge University Press: 17 November 2021
We investigate, for given positive integers a and b, the least positive integer
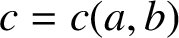 $c=c(a,b)$
such that the quotient
$c=c(a,b)$
such that the quotient
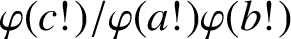 $\varphi (c!\kern-1.2pt)/\varphi (a!\kern-1.2pt)\varphi (b!\kern-1.2pt)$
is an integer. We derive results on the limit of
$\varphi (c!\kern-1.2pt)/\varphi (a!\kern-1.2pt)\varphi (b!\kern-1.2pt)$
is an integer. We derive results on the limit of
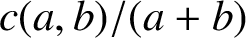 $c(a,b)/(a+b)$
as a and b tend to infinity and show that
$c(a,b)/(a+b)$
as a and b tend to infinity and show that
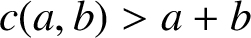 $c(a,b)>a+b$
for all pairs of positive integers
$c(a,b)>a+b$
for all pairs of positive integers
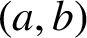 $(a,b)$
, with the exception of a set of density zero.
$(a,b)$
, with the exception of a set of density zero.
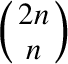 $\left(\genfrac{}{}{0pt}{}{2n}{n}\right)$
’, Math. Comp. 29 (1975), 83–92.CrossRefGoogle Scholar
$\left(\genfrac{}{}{0pt}{}{2n}{n}\right)$
’, Math. Comp. 29 (1975), 83–92.CrossRefGoogle Scholar