No CrossRef data available.
Article contents
ON A PROBLEM ABOUT ADDITIVE REPRESENTATION FUNCTIONS
Published online by Cambridge University Press: 08 February 2022
Abstract
For a set A of positive integers and any positive integer n, let
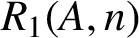 $R_{1}(A, n)$
,
$R_{1}(A, n)$
,
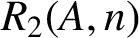 $R_{2}(A,n)$
and
$R_{2}(A,n)$
and
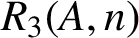 $R_{3}(A,n)$
denote the number of solutions of
$R_{3}(A,n)$
denote the number of solutions of
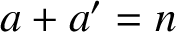 $a+a^{\prime }=n$
with
$a+a^{\prime }=n$
with
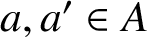 $a, a^{\prime }\in A$
and the additional restriction that
$a, a^{\prime }\in A$
and the additional restriction that
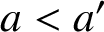 $a<a^{\prime }$
for
$a<a^{\prime }$
for
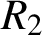 $R_{2}$
and
$R_{2}$
and
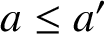 $a\leq a^{\prime }$
for
$a\leq a^{\prime }$
for
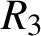 $R_{3}$
. We consider Problem 6 of Erdős et al. [‘On additive properties of general sequences’, Discrete Math. 136 (1994), 75–99] about locally small and locally large values of
$R_{3}$
. We consider Problem 6 of Erdős et al. [‘On additive properties of general sequences’, Discrete Math. 136 (1994), 75–99] about locally small and locally large values of
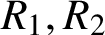 $R_{1}, R_{2}$
and
$R_{1}, R_{2}$
and
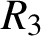 $R_{3}$
.
$R_{3}$
.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported by the National Natural Science Foundation of China (Grant No. 11971033) and top talents project of Anhui Department of Education (Grant No. gxbjZD05).



