No CrossRef data available.
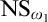 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 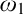 $\omega _1$-Dense” from Large Cardinals
$\omega _1$-Dense” from Large CardinalsPublished online by Cambridge University Press: 18 March 2025
We answer a question of Woodin [3] by showing that “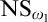 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 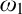 $\omega _1$-dense” holds in a stationary set preserving extension of any universe with a cardinal
$\omega _1$-dense” holds in a stationary set preserving extension of any universe with a cardinal 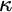 $\kappa $ which is a limit of
$\kappa $ which is a limit of 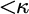 ${<}\kappa $-supercompact cardinals. We introduce a new forcing axiom
${<}\kappa $-supercompact cardinals. We introduce a new forcing axiom 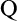 $\mathrm {Q}$-Maximum, prove it consistent from a supercompact limit of supercompact cardinals, and show that it implies the version of Woodin’s
$\mathrm {Q}$-Maximum, prove it consistent from a supercompact limit of supercompact cardinals, and show that it implies the version of Woodin’s 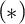 $(*)$-axiom for
$(*)$-axiom for 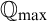 $\mathbb Q_{\mathrm {max}}$. It follows that
$\mathbb Q_{\mathrm {max}}$. It follows that 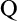 $\mathrm {Q}$-Maximum implies “
$\mathrm {Q}$-Maximum implies “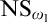 $\mathrm {NS}_{\omega _1}$ is
$\mathrm {NS}_{\omega _1}$ is 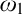 $\omega _1$-dense.” Along the way we produce a number of other new instances of Asperó–Schindler’s
$\omega _1$-dense.” Along the way we produce a number of other new instances of Asperó–Schindler’s 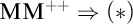 $\mathrm {MM}^{++}\Rightarrow (*)$ (see [1]).
$\mathrm {MM}^{++}\Rightarrow (*)$ (see [1]).
To force 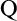 $\mathrm {Q}$-Maximum, we develop a method which allows for iterating
$\mathrm {Q}$-Maximum, we develop a method which allows for iterating 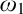 $\omega _1$-preserving forcings which may destroy stationary sets, without collapsing
$\omega _1$-preserving forcings which may destroy stationary sets, without collapsing 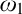 $\omega _1$. We isolate a new regularity property for
$\omega _1$. We isolate a new regularity property for 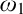 $\omega _1$-preserving forcings called respectfulness which lies at the heart of the resulting iteration theorem.
$\omega _1$-preserving forcings called respectfulness which lies at the heart of the resulting iteration theorem.
In the second part, we show that the 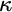 $\kappa $-mantle, i.e., the intersection of all grounds which extend to V via forcing of size
$\kappa $-mantle, i.e., the intersection of all grounds which extend to V via forcing of size 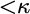 ${<}\kappa $, may fail to be a model of
${<}\kappa $, may fail to be a model of 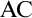 $\mathrm {AC}$ for various types of
$\mathrm {AC}$ for various types of 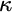 $\kappa $. Most importantly, it can be arranged that
$\kappa $. Most importantly, it can be arranged that 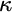 $\kappa $ is a Mahlo cardinal. This answers a question of Usuba [2].
$\kappa $ is a Mahlo cardinal. This answers a question of Usuba [2].
Abstract prepared by Andreas Lietz
E-mail: [email protected].
URL: https://andreas-lietz.github.io/resources/PDFs/AJourneyGuidedByThe Stars.pdf.
Supervised by Ralf Schindler.