The thesis uses various approaches to explore the algorithmic complexity of families of subsets of natural numbers. One of these approaches involves investigating upper semilattices of computable numberings of a given family and their complexity in different hierarchies. These semilattices, known as Rogers semilattices, can help distinguish different structural properties of families of partial computable functions and computably enumerable sets. As a result, by using Rogers semilattices of computable numberings, we can measure the algorithmic complexity of the corresponding family.

In the first part of thesis, we focus on limitwise monotonic numberings for families of limitwise monotonic sets and define their Rogers semilattices. The chapter investigates global invariants that show differences in the algebraic and elementary properties of the Rogers semilattices of families of sets from arithmetical hierarchy and Rogers semilattices of limitwise monotonic numberings. Such invariants include cardinality, laticeness, and types of isomorphism.

Within the second part of thesis, we explore the different forms of isomorphism exhibited by Rogers semilattices of families of sets in the analytical hierarchy. Additionally, we take into account various set-theoretic assumptions. Our research demonstrates that, when set-theoretic assumption known as Projective Determinacy is assumed, there exist an infinite number of non-isomorphic Rogers semilattices at each 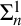$\Sigma _n^1$-level of the analytical hierarchy.

I would also like to acknowledge the Grant of Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (AP19676989) and the Nazarbayev University Faculty Development Grant (N021220FD3851) for funding this research.

Abstract prepared by Zhansaya Tleuliyeva

[email protected].

URL: http://nur.nu.edu.kz/handle/123456789/7769.