Published online by Cambridge University Press: 15 January 2014
The Euclidean algorithm on the natural numbers ℕ = {0,1,…} can be specified succinctly by the recursive program
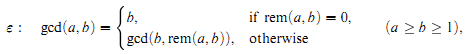
where rem(a, b) is the remainder in the division of a by b, the unique natural number r such that for some natural number q,

It is an algorithm from (relative to) the remainder function rem, meaning that in computing its time complexity function cε (a, b), we assume that the values rem(x, y) are provided on demand by some “oracle” in one “time unit”. It is easy to prove that
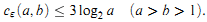
Much more is known about cε(a, b), but this simple-to-prove upper bound suggests the proper formulation of the Euclidean's (worst case) optimality among its peers—algorithms from rem:
Conjecture. If an algorithm α computes gcd (x,y) from rem with time complexity cα (x,y), then there is a rational number r > 0 such that for infinitely many pairs a > b > 1, cα (a,b) > r log2a.