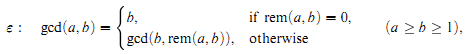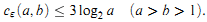Research Article
Forcing in Proof Theory
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 305-333
-
- Article
- Export citation
Notes on Quasiminimality and Excellence
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 334-366
-
- Article
- Export citation
Transfinite Progressions: A Second Look at Completeness
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 367-389
-
- Article
- Export citation
Is the Euclidean Algorithm Optimal Among its Peers?
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 390-418
-
- Article
- Export citation
Reviews
Risto Vilkko. A hundred years of logical investigations. Reform efforts of logic in Germany 1781–1879. Mentis, Paderborn, 2002, 208 pp.
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 419-421
-
- Article
- Export citation
V. A. Bazhanov. Ocerki sotsialnoj istorii logiki v Rossii [Sketches of the social history of logic in Russia]. Izdatel'stvo Srednevolzhskogo nauchnogo tsentra, Simbirsk-Ul'yanovsk, 2002, 124 pp.
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 421-423
-
- Article
- Export citation
Dennis E. Hesseling. Gnomes in the fog. The reception of Brouwer's intuitionism in the 1920s. Science Networks. Historical Studies, vol. 28. Birkhäuser, Boston, 2003, xxiii + 447 pp.
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 423-427
-
- Article
- Export citation
Joseph Y. Halpern. Reasoning about Uncertainty. MIT Press Cambridge, MA, 2003, xiv + 483 pp.
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 427-429
-
- Article
- Export citation
Gabriel Debs and Jean Saint Raymond. Compact covering mappings and cofinal families of compact subsets of a Borel set. Fundamenta Mathematicae, vol. 167, no. 3 (2001), pp. 213–249. - Gabriel Debs and Jean Saint Raymond. Compact covering mappings between Borel spaces. Acta Universitatis Carolinae. Mathematica et Physica, vol. 40, no. 2 (1999), pp. 53–64. - Gabriel Debs and Jean Saint Raymond. Cofinal and subsets of ωω . Fundamenta Mathematicae, vol. 159, no. 2 (1999), pp. 161–193. - Gabriel Debs and Jean Saint Raymond. Compact-covering-properties of finite-to-one mappings. Topology and its Applications, vol. 81, no. 1 (1997), pp. 55–84. - Gabriel Debs and Jean Saint Raymond. Some applications of game determinacy. Acta Universitatis Carolinae. Mathematica et Physica, vol. 37, no. 2 (1996), pp. 7–23. - Gabriel Debs and Jean Saint Raymond. Compact covering and game determinacy. Topology and its Applications, vol. 68, no. 2 (1996), pp. 153–185. - Gabriel Debs and Jean Saint Raymond. Compact covering mappings between Borel sets and the size of constructible reals. Transactions of the American Mathematical Society, vol. 356, no. 1 (2004), pp. 73–117.
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 430-434
-
- Article
- Export citation
Obituary
In Memoriam: Willem Johannes Blok 1947–2003
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 435-437
-
- Article
-
- You have access
- Export citation
Meeting Report
2004 Spring Meeting of the Association for Symbolic Logic
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 438-446
-
- Article
- Export citation
2004 Annual Conference of the Australasian Association for Logic
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 447-451
-
- Article
- Export citation
Other
Notices
-
- Published online by Cambridge University Press:
- 15 January 2014, pp. 452-456
-
- Article
- Export citation
Front matter
BSL volume 10 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 July 2016, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BSL volume 10 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 July 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation