Introduction
Governments can increase welfare by addressing market failures and providing public goods. In addition, they often try to make constituents better informed, hoping to raise welfare by inducing consumers to make better decisions. For example, government agencies such as the Food and Drug Association (FDA) and the Consumer Protection Agency disseminate recommendations and guidelines. In addition, firms are increasingly required to disclose information that is deemed relevant to consumers, so credit card companies must disclose important details about the products they offer and food producers must adhere to labeling regulations.
Yet processing this information requires consumers’ attention. If attention is unlimited, more information is weakly better, so any regulation that mandates disclosure cannot do harm. There is growing evidence that consumers’ attention is limited, however (see, e.g. Chetty et al., Reference Chetty, Looney and Kroft2009; Dellavigna & Pollet, Reference Dellavigna and Pollet2009; Abaluck & Gruber, Reference Abaluck and Gruber2011), which makes the welfare consequences of regulation that mandates disclosure a priori less clear, as consumer attention devoted to one piece of information may crowd out attention to others. The literature on rational inattention analyzes how a decision-maker with limited attention allocates it across various passive sources of information (e.g. Sims, Reference Sims2003; Wiederholt, Reference Wiederholt2010). The core idea in this paper is that consumers’ limited attention gives information providers, such as firms, incentives to be active. To be more precise, when a consumer's attention is limited, her ultimate purchasing decisions may hinge on what she pays attention to; this, in turn, incentivizes firms to engage in attention manipulation – that is, strategic actions to influence how she allocates her attention. This is distinct from, and operates on top of, any incentive to manipulate the substance of consumer-facing communication.
The first part of the paper shows that, in the presence of attention manipulation, competitive information supply from firms competing for attention can reduce consumer knowledge by causing information overload. In the second part of the paper I show that a single information provider, such as a firm mandated to disclose information, may deliberately induce information overload to conceal information. Thus, requiring a firm to disclose all hidden, undesirable features of its product may have no impact on social welfare; the firm will simply disclose these features along with an avalanche of irrelevant information. But if full disclosure policies can backfire, intuition suggests that there is an easy fix: simply to mandate not only what firms disclose, but also how it should be disclosed. The paper's third result is a disconcerting one, however: mandating that firms provide easy-to-understand information about the products they sell will induce ‘complexification’ of the underlying products themselves. This is essential as it limits the potential welfare gains from mandated information provision; in fact, complexification can eradicate all welfare gains. Together, these findings demonstrate that taking attention manipulation into account has important implications for the design of consumer protection regulation by suggesting a role for rules that restrict communication, mandate not only the content but also the format of disclosure and regulate product design.
These findings arise in a theoretical framework of information exchange between one consumer (the decision-maker; henceforth the ‘DM’) and various suppliers of information (firms; henceforth ‘experts’). To capture attention manipulation, I want to permit the experts to be active, in the sense that they make persuasion effort choices that, in turn, affect the optimal attention allocation of the DM. I depart from the framework of Dewatripont and Tirole (Reference Dewatripont and Tirole2005), who model a DM interacting with a single expert. The DM considers taking an action with an uncertain payoff to her, but that would surely benefit the expert (e.g. buying a good from the expert). Before the DM decides, she can communicate with the expert. Communication is a moral-hazard-in-team problem: the more attention the DM pays to the expert and the greater the expert's effort, the more likely it is that information is exchanged successfully between them. Dewatripont and Tirole (Reference Dewatripont and Tirole2005) refer to this as issue-relevant communication, because it concerns the DM's actual benefits from the action. Importantly, the expert does not know what conclusion the DM will draw from the information he provides; he only knows that it may affect her decision.Footnote 1 In addition, Dewatripont and Tirole (Reference Dewatripont and Tirole2005) include a pre-play stage in which cue communication takes place. This does not concern the actual benefits associated with the action, but rather the decision's ex ante appeal – that is, the likelihood that (issue-relevant communication will show that) the action is beneficial.
To analyze attention manipulation, I introduce multitasking into this framework. A single DM (she) considers several binary actions and can communicate with one distinct expert (he) on each of them. Each of these issue-relevant information exchanges is a moral-hazard-in-team's problem and the DM now faces a multitasking problem because she must divide her limited attention between the various experts. In the first part of next section, I show that, in this framework, attention substitution leads to externalities that I refer to as attention crowding out: each expert ignores the effects of his chosen persuasion effort on the attention that the DM devotes to other experts. Interestingly, an expert benefits or suffers from crowding out depending on whether he believes that attention from the DM will raise or lower the likelihood that she takes the action from which he benefits. This makes an expert's expected payoff non-monotonic in the appeal of other experts’ proposed actions.
In the second part of next section, I allow each action's ex ante appeal to be unobserved by the DM and add a stage before issue-relevant communication in which cue communication can take place. Specifically, each expert can, at a cost, send hard information about his proposed action's appeal to the DM and she can process this cue at a cost. Intuitively, in the presence of competition between experts for the DM's attention, cue communication takes place first and helps the DM select which experts (actions) to devote attention to in the second stage. Cue communication thus shapes the set of actions on which the DM ends up deliberating. For this reason, I say that cue communication takes place in the ‘selection stage’ and issue-relevant communication in the subsequent ‘deliberation stage’.
I analyze how the DM's welfare changes as the cost of sending cues – or proposing actions to the DM – falls and, consequently, more experts seek attention and more choices enter the picture. Initially, she benefits from the fact that she has more actions from which to choose. But as entry becomes cheaper, it becomes profitable for experts who propose less-appealing actions to enter. As a result, the average quality of the proposed actions deteriorates and the DM must read cues, at a cost, to find the attractive ones. Eventually, as the supply escalates, screening ceases to be worthwhile to her and she picks proposed actions for deliberation randomly.
Thus, at a certain point, as the competition for the DM's attention increases and she gets more information, she processes less of it – or tunes out – and fares worse. I refer to this as information overload. Its immediate cause is that the quality of the proposed actions decreases with the quantity; actions worthy of deliberation become the proverbial needle in a haystack. The deeper cause, though, is negative externalities: entry is individually rational for each expert, even as it complicates the selection problem for the DM and spoils overall communication. A DM with limited attention may hence want to limit access to her attention space, even if that reduces her choice set. She faces a trade-off between comprehensiveness and comprehensibility.
The subsequent section reinterprets the framework to capture a DM who communicates with a single expert on one action that has several aspects. In the deliberation stage, the DM's multi-tasking problem now stems from the fact that the DM must decide how to allocate her scarce attention across the various aspects of the action. Recall that, in the selection stage, in the ‘multiple experts’ setting analyzed in the next section, the DM is unsure of each action's ex ante appeal. The analogue in the ‘single expert’ setting is that the DM is unsure which aspects of the (single) action are financially relevant and hence worth devoting attention to in the deliberation stage.
The analysis in the ‘single expert’ setting picks up on the information overload result from the ‘multiple experts’ setting and shows that a single expert may induce this outcome. Specifically, in the ‘multiple experts’ setting, information overload resulted from various experts’ competition for attention. I then show that a single expert who faces no competition for the DM's attention, but who can communicate with the DM about multiple aspects of the action for which he advocates, may strategically induce information overload in the DM. This arises when the expert wants to divert attention from relevant aspects that are ‘unfavorable’ in the sense that, if the DM learns more about those aspects, she may not take the action. Of course, if it were up to the expert, he would not bring up any such unfavorable aspect – that is, he would not send any cue about it. But sometimes the expert cannot or may not withhold such information (e.g. due to laws that mandate disclosure of relevant information). I show that, in response to such a disclosure mandate, the expert chooses to inundate the DM with cues relating mostly to irrelevant aspects of the action. This induces information overload, which, in turn, effectively conceals the inconvenient aspects that the firm was mandated to disclose in the first place. In other words, the expert shares superfluous information to strategically induce information overload, which essentially obfuscates the DM. When consumers’ attention is limited, simple disclosure rules can thus be completely ineffective and have no impact on social welfare.
But if disclosure mandates can backfire because firms can induce information overload, intuition suggests an immediate solution: to mandate not only what firms disclose, but also that it be disclosed in an easy-to-understand way. The final part of the analysis shows, however, that requiring a firm to provide easy-to-understand information about a product it sells can induce a ‘complexification’ of the underlying product itself. I show this by extending the model with a single expert to allow the DM's payoff from the (single) action to be composed of many components and to allow the expert to manipulate that composition so long as the total payoff stays constant. Intuitively, such payoff-equivalent variations amount to changing the number of financially relevant aspects of the product. This gives the expert yet another tactic with which to thwart learning: the expert can force the DM to understand more details of the action, or product, to grasp its total payoff; in other words, he can make it more complex. Complexification ensures that an increasing amount of relevant information slips the DM's attention and, by the same token, that whatever she can learn in the deliberation stage is so trivial that it no longer affects her decision. In a nutshell, even if she fully understands all the aspects on which she can deliberate, she will always do what she would have done anyway. Complexification thus has the same welfare consequences as inducing information overload – it can eradicate all intended welfare gains from mandated information provision. But complexity is a more delicate issue for regulation: unlike strategic information overload, it cannot be tackled at the level of communication, information and disclosure; it may call for intervention in product design.
This paper builds on and contributes to several strands of the literature. First, I advance recent work on two-sided communication as a moral-hazard-in-teams problem, where the ‘softness’ of information is intermediate and endogenous (Dewatripont & Tirole, Reference Dewatripont and Tirole2005), by introducing multiple experts that vie for a DM's attention.Footnote 2 Competition for attention leads to attention substitution, which in turn invites attention manipulation. More generally, this relates to a number of studies that examine how a DM communicates with multiple experts or with a single expert on multiple topics. Krishna and Morgan (Reference Krishna and Morgan2001), Battaglini (Reference Battaglini2002) and Ambrus and Takahashi (Reference Ambrus and Takahashi2008) study competing experts in a soft information setting. In contrast, Milgrom and Roberts (Reference Milgrom and Roberts1986) and Gentzkow and Kamenica (Reference Gentzkow and Kamenica2017) study multiple experts in a hard information setting, and Chakraborty and Harbaugh (Reference Chakraborty and Harbaugh2007, Reference Chakraborty and Harbaugh2010) study soft communication between a DM and one expert on several topics. In these papers, competition or multiplicity typically increases the amount of knowledge the DM gains.Footnote 3 Kartik et al. (Reference Kartik, Xu Lee and Suen2017) endogenize information acquisition in a hard information setting with multiple experts and show that adding more experts can reduce the DM's welfare. The mechanism driving this result – that adding experts reduces each expert's incentive to acquire costly information – is, however, distinct from information overload. In my setting, there is no information acquisition; instead, central to my finding that more information can reduce a DM's knowledge is that experts manipulate not only the substance of communication, but also the DM's attention allocation. This suggests that limits to attention are important in determining whether individuals stand to benefit from a more competitive, or greater, information supply.Footnote 4
Second, my focus on attention limitations relates to recent work in the industrial organization literature with attention-constrained consumers. Spiegler and Eliaz (Reference Spiegler and Eliaz2011a, Reference Spiegler and Eliaz2011b) and de Clippel et al. (Reference de Clippel, Eliaz and Rozen2014) analyze a setting where consumers pay attention only to a subset of available options and firms can manipulate this ‘consideration set’ through marketing or price setting. Hefti (Reference Hefti2017) studies a similar but more general setting with imperfect price competition and derives a mechanism akin to the information overload result presented in the next section (and in Persson, Reference Persson2013), suggesting that this result is robust to various modeling assumptions – so long as consumers’ attention is limited. The two key results presented in the subsequent section relate to Carlin (Reference Carlin2009), Wilson (Reference Wilson2010) and Ellison and Wolitzky (Reference Ellison and Wolitzky2012), whose papers model obfuscation or complexification as a strategic choice firms make to raise search costs in settings with optimal consumer search.Footnote 5 In these papers, firms’ incentives to raise these search costs stem from competition between firms. The present paper shows that obfuscation and complexification can be individually rational even when a single firm operates in the absence of competition, if it is subjected to disclosure regulation. In addition, the paper makes a distinction between obfuscation – which alters communication about a product without altering the product itself – and complexification – which affects the product characteristics per se. While the consumer welfare consequences of these phenomena are similar, the distinction has crucial implications for optimal disclosure regulation.
Third, Bordalo et al. (Reference Bordalo, Gennaioli and Shleifer2012, Reference Bordalo, Gennaioli and Shleifer2013) model the attributes to which an individual's attention is drawn when it is limited: attention is unproportionally allocated to salient issues. I instead focus on how, when individuals have limited attention, market participants’ strategically act to make a certain attribute of a good salient or invisible, depending on whether the market participant wants to conceal or emphasize the attribute. Put differently, I allow interested parties to influence the relative salience of a product's attributes. This relates to Bordalo et al. (Reference Bordalo, Gennaioli and Shleifer2016) and Manzini and Mariotti (Reference Manzini and Mariotti2017), who study competitive markets where the salience of goods’ characteristics is endogenously determined.
Many experts competing for limited attention
In this section, I introduce the multiple expert setting and analyze, in turn, the deliberation stage and the selection stage.
The deliberation stage
Set-up I introduce multiple senders, or experts, into the framework proposed by Dewatripont and Tirole (Reference Dewatripont and Tirole2005). A DM faces two simultaneous decisions, i = 1, 2.Footnote 6 Each decision i concerns whether to take a distinct action, A i. For each decision, there is a distinct expert who gets a deterministic payoff d > 0 if the DM takes the action and zero otherwise. The DM's payoff ![]() $\tilde x_i $ from A i takes the value
$\tilde x_i $ from A i takes the value ![]() $\bar{x}{\rm \;} \gt \; 0$ with probability α i and otherwise the value x < 0. The probability α i is common knowledge. The larger the α i, the more attractive A i seems to the DM and the more aligned are her interests with those of the expert vested in A i. Everyone is risk-neutral. In the absence of additional information, the DM takes A i if and only if its expected payoff is positive:
$\bar{x}{\rm \;} \gt \; 0$ with probability α i and otherwise the value x < 0. The probability α i is common knowledge. The larger the α i, the more attractive A i seems to the DM and the more aligned are her interests with those of the expert vested in A i. Everyone is risk-neutral. In the absence of additional information, the DM takes A i if and only if its expected payoff is positive: ![]() $\alpha _i \gt \alpha ^{\rm *} \equiv \displaystyle{{ - \underline{x}} / \lpar {\bar x - \underline{x}}\rpar } $.Footnote 7
$\alpha _i \gt \alpha ^{\rm *} \equiv \displaystyle{{ - \underline{x}} / \lpar {\bar x - \underline{x}}\rpar } $.Footnote 7
Before making any decision, the DM can learn more about the actions. For each action, the vested expert can provide information and the DM can devote attention to processing this information. Through such communication, the DM can learn the realization of ![]() $\tilde x_i $. The expert himself knows neither whether
$\tilde x_i $. The expert himself knows neither whether ![]() $\tilde x_i = \bar x$ or
$\tilde x_i = \bar x$ or ![]() $\tilde x_i = \underline{x} $ nor whether the (truthful) information he provides will help the DM find out. Nevertheless, his information may persuade the DM to take A i even though α i < α*, since the DM may find out that
$\tilde x_i = \underline{x} $ nor whether the (truthful) information he provides will help the DM find out. Nevertheless, his information may persuade the DM to take A i even though α i < α*, since the DM may find out that ![]() $\tilde x_i = \bar x$. The probability that the DM learns
$\tilde x_i = \bar x$. The probability that the DM learns ![]() $\tilde x_i $ is given by p(s i, r i), where s i and r i are, respectively, the expert's effort to communicate about A i and the attention that the DM devotes to learning about A i.
$\tilde x_i $ is given by p(s i, r i), where s i and r i are, respectively, the expert's effort to communicate about A i and the attention that the DM devotes to learning about A i.
Assumption
The function p(s i, r i) is twice continuously differentiable on [0, 1]2, with p(0, 0) = 0 and p(1, 1) = 1. It is strictly concave and satisfies p 1( · ) > 0, p 2( · ) > 0, p 12( · ) > 0 and the Inada condition ![]() $\forall s_i \in \left[ {0,1} \right],$ p 2( · ) → 0 as r i → 1 and p 2( · ) → ∞ as r i → 0.Footnote 8
$\forall s_i \in \left[ {0,1} \right],$ p 2( · ) → 0 as r i → 1 and p 2( · ) → ∞ as r i → 0.Footnote 8
Successful communication is more likely the more effort the expert devotes to persuasion (p 1( · ) > 0) and the more attention the DM devotes to his message (p 2( · ) > 0). In short, communication is a team effort. Because communication efforts are complements (p 12( · ) > 0), an expert's return from expending effort is higher when the DM listens more attentively and the DM's return from paying attention is higher when the expert makes a greater effort to explain. The formulation encompasses communication technologies with the property p(0, r i) ≠ 0: even if an expert makes no effort to transmit information to the DM, it is possible for her to find the relevant information by herself.Footnote 9
Communication is costly to both parties. The DM's attention is scarce, ![]() $\mathop \sum \nolimits_i r_i \le 1$, so the cost is attention substitution: paying more attention to one action necessarily comes at the expense of others. An expert's cost of persuasion effort is given by c(s i).
$\mathop \sum \nolimits_i r_i \le 1$, so the cost is attention substitution: paying more attention to one action necessarily comes at the expense of others. An expert's cost of persuasion effort is given by c(s i).
Assumption
The function c(s i) is twice continuously differentiable on (0, 1) and satisfies c′( · ) > 0 and c″( · ) > 0 as well as the Inada conditions c′( · ) → 0 as s i → 0 and c′( · ) ![]() $ \to $ ∞ as s i → 1.
$ \to $ ∞ as s i → 1.
The persuasion efforts and the attention allocation are chosen simultaneously and non-cooperatively. I refer to the above game as the deliberation stage.
I determine the Nash equilibrium for this game and then analyze how the experts affect each other in equilibrium.
Lemma 1
If α1, α2 ≤ α*, there is a unique equilibrium ![]() $\left( {{\rm r}_1^{\rm *}, {\rm s}_1^{\rm *}, {\rm s}_2^{\rm *}} \right)$, which is interior. If α1 ≤ α*< α2, there is a unique equilibrium
$\left( {{\rm r}_1^{\rm *}, {\rm s}_1^{\rm *}, {\rm s}_2^{\rm *}} \right)$, which is interior. If α1 ≤ α*< α2, there is a unique equilibrium ![]() $\left( {{\rm r}_1^{\rm *}, {\rm s}_1^{\rm *}, 0} \right)$. If α1, α2 > α*, there is a unique equilibrium
$\left( {{\rm r}_1^{\rm *}, {\rm s}_1^{\rm *}, 0} \right)$. If α1, α2 > α*, there is a unique equilibrium ![]() $\left( {{\rm r}_1^{\rm *}, 0,0} \right)$.
$\left( {{\rm r}_1^{\rm *}, 0,0} \right)$.
The proof of this lemma, as well as proofs of all subsequent formal results, is available in the Online Appendix.
An expert's behavior hinges on whether the DM uses an opt-in rule or an opt-out rule for the decision in which he is vested. When αi ≤ α*, the DM uses an opt-in rule with respect to A i. Her default is not to take A i, but she departs from this default – opts in – if she learns that ![]() $\tilde x_i = \bar x$. Hence, expert i has an incentive to communicate with her. Thus, when α1, α2 ≤ α*, each expert solves
$\tilde x_i = \bar x$. Hence, expert i has an incentive to communicate with her. Thus, when α1, α2 ≤ α*, each expert solves
and the DM's problem is
In the unique equilibrium, both experts communicate and the DM pays attention to both. The Inada condition rules out corners; global concavity of p(s i, r i) guarantees uniqueness.
In contrast, when αi > α*, the receiver uses an opt-out rule with respect to A i. Her default is to take A i, but she departs from this default – opts out – if she learns that ![]() $\tilde x_i = \underline{x} $. Because communication can only persuade the DM not to take A i, expert i makes no effort. The DM can nevertheless devote attention to A i; that is, she can engage in (one-sided) information acquisition. If α1 ≤ α*, α2 > α*, her problem is
$\tilde x_i = \underline{x} $. Because communication can only persuade the DM not to take A i, expert i makes no effort. The DM can nevertheless devote attention to A i; that is, she can engage in (one-sided) information acquisition. If α1 ≤ α*, α2 > α*, her problem is
In the unique equilibrium, expert 1 exerts effort, expert 2 is passive and the DM communicates with expert 1 about A 1 and devotes some attention to acquiring information about A 2. The distinction between one-sided and two-sided communication arises endogenously.
Crowding out How well an expert fares in the deliberation stage depends not only on how attractive his own action seems to the DM, but also on the other experts’ attractiveness.
Proposition 1 (crowding out)
Fix expert 2's attractiveness, α 2. If expert 2 wants the DM's attention (α 2 ≤ α*), his expected utility is a strictly decreasing function of the attention given to expert 1, ![]() $r_1^* \left( {\alpha _1} \right)$. If expert 2 does not want the DM's attention (α 2 > α*), his expected utility is a strictly increasing function of the attention given to expert 1,
$r_1^* \left( {\alpha _1} \right)$. If expert 2 does not want the DM's attention (α 2 > α*), his expected utility is a strictly increasing function of the attention given to expert 1, ![]() $r_1^* \left( {\alpha _1} \right)$.
$r_1^* \left( {\alpha _1} \right)$.
As ![]() $r_2^* \left( {\alpha _1} \right) = 1 - r_1^* \left( {\alpha _1} \right)$, a change in α1 that causes the DM to pay more attention to expert 1 in equilibrium crowds out attention to expert 2. When expert 2 wants the DM's attention, this crowding out harms him; otherwise, it benefits him. Thus, the presence of expert 1 imposes a negative or positive externality on expert 2 and the size of this externality is captured by
$r_2^* \left( {\alpha _1} \right) = 1 - r_1^* \left( {\alpha _1} \right)$, a change in α1 that causes the DM to pay more attention to expert 1 in equilibrium crowds out attention to expert 2. When expert 2 wants the DM's attention, this crowding out harms him; otherwise, it benefits him. Thus, the presence of expert 1 imposes a negative or positive externality on expert 2 and the size of this externality is captured by ![]() $r_1^* \left( {\alpha _1} \right)$.
$r_1^* \left( {\alpha _1} \right)$.
Corollary 1
Fix expert 2's attractiveness, α 2. Expert 2's expected utility is non-monotonic in the attractiveness of expert 1, α 1.
This follows from the fact that the attention the DM devotes to expert 1 in equilibrium, ![]() $r_1^{\rm *} \left( {\alpha _1} \right)$, is non-monotonic in α 1:
$r_1^{\rm *} \left( {\alpha _1} \right)$, is non-monotonic in α 1: ![]() $r_1^{\rm *} \left( {\alpha _1} \right)$ increases for α 1 ∈ (0, α*), falls at α* and decreases for α 1 ∈ (α*, 1). If expert 2 wants the DM's attention (α 2 ≤ α*),
$r_1^{\rm *} \left( {\alpha _1} \right)$ increases for α 1 ∈ (0, α*), falls at α* and decreases for α 1 ∈ (α*, 1). If expert 2 wants the DM's attention (α 2 ≤ α*), ![]() ${\bi E}U_{Exp_2} \left( {\alpha _1} \right)$ is negatively related to
${\bi E}U_{Exp_2} \left( {\alpha _1} \right)$ is negatively related to ![]() $r_1^{\rm *} \left( {\alpha_1} \right)$; otherwise, the reverse holds. This is illustrated in Figure 1.
$r_1^{\rm *} \left( {\alpha_1} \right)$; otherwise, the reverse holds. This is illustrated in Figure 1.
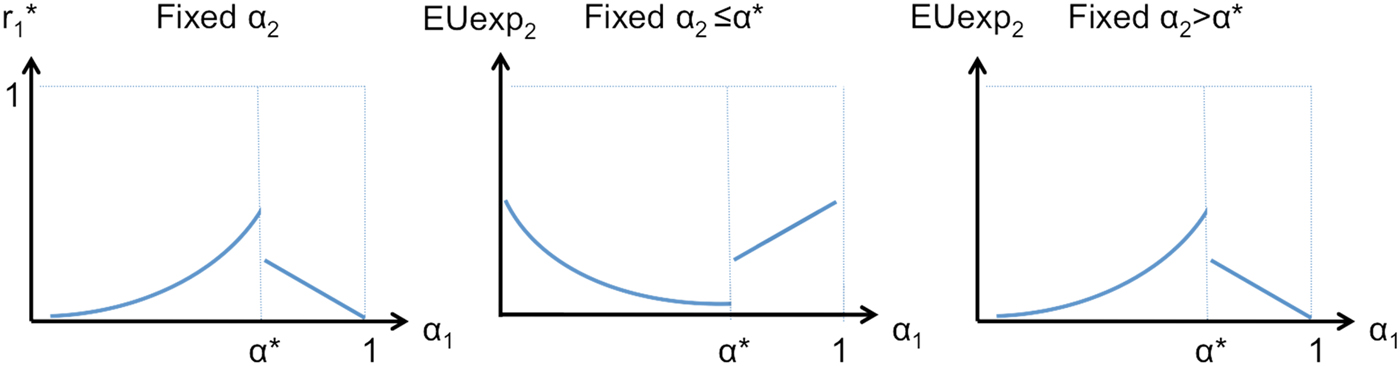
Figure 1. Crowding out. The DM's attention devoted to expert 1 in equilibrium ![]() $r_1^* \left( {\alpha _1} \right)$ for a given α 2 is non-monotonic in expert 1's attractiveness (left panel). This makes expert 2's utility non-monotonic in α 1: when expert 2 desires attention (α 2 ≤ α*),
$r_1^* \left( {\alpha _1} \right)$ for a given α 2 is non-monotonic in expert 1's attractiveness (left panel). This makes expert 2's utility non-monotonic in α 1: when expert 2 desires attention (α 2 ≤ α*), ![]() $r_1^* \left( {\alpha _1} \right)$ represents a negative externality on expert 2, so EU Exp2(α 1) is negatively related to
$r_1^* \left( {\alpha _1} \right)$ represents a negative externality on expert 2, so EU Exp2(α 1) is negatively related to ![]() $r_1^* \left( {\alpha _1} \right)\; $(middle panel). When expert 2 does not desire attention (α2 > α*),
$r_1^* \left( {\alpha _1} \right)\; $(middle panel). When expert 2 does not desire attention (α2 > α*), ![]() $r_1^* \left( {\alpha _1} \right)$ represents a positive externality on expert 2, so EU Exp2(α 1) is positively related to
$r_1^* \left( {\alpha _1} \right)$ represents a positive externality on expert 2, so EU Exp2(α 1) is positively related to ![]() $r_1^* \left( {\alpha _1} \right)$ (right panel).
$r_1^* \left( {\alpha _1} \right)$ (right panel).
The selection stage
We now add a pre-play stage by introducing cue communication, as in Dewatripont and Tirole (Reference Dewatripont and Tirole2005).
Set-up The DM can pay attention to two distinct actions in the deliberation stage.Footnote 10 When more than two experts seek the DM's attention, selection becomes an important issue. To capture this, I add a pre-play stage in which the DM must select at most two experts for the deliberation stage. I refer to the pre-play stage as the ‘selection stage’.Footnote 11 ![]() $N = N_{\bar \alpha} + N_{\underline{\alpha}} $ experts can enter the competition to be selected. Of these,
$N = N_{\bar \alpha} + N_{\underline{\alpha}} $ experts can enter the competition to be selected. Of these, ![]() $N_{\bar \alpha} $ propose actions of high quality
$N_{\bar \alpha} $ propose actions of high quality ![]() $\left( {\alpha = \bar \alpha} \right)$ and N α; of low quality
$\left( {\alpha = \bar \alpha} \right)$ and N α; of low quality ![]() $\left( {\alpha = \underline{\alpha} \lt \bar \alpha} \right)$.
$\left( {\alpha = \underline{\alpha} \lt \bar \alpha} \right)$. ![]() $N_{\bar \alpha} \gt t$ is finite; N α is infinite. I set parameters such that all experts want attention,
$N_{\bar \alpha} \gt t$ is finite; N α is infinite. I set parameters such that all experts want attention, ![]() $\underline{\alpha} \lt \bar \alpha \lt \alpha ^{\rm *} $.
$\underline{\alpha} \lt \bar \alpha \lt \alpha ^{\rm *} $.
As in Dewatripont and Tirole (Reference Dewatripont and Tirole2005), each expert's quality is his private information. Hence, an expert may be willing to signal the quality of his action if it helps him get selected and the DM may be willing to read such signals before choosing on which actions to deliberate; that is, with which experts to communicate. Specifically, at cost q S > 0, an expert can send a cue (signal) that contains hard information about the quality of his action. Upon receiving a cue, the DM decides whether to process it, at cost q R >0, to learn the action's quality. No expert can be selected without having sent a cue; hence, q S can be thought of as an entry cost. As I explain below, this last assumption is not crucial.
I solve this game, deliberation stage plus selection stage, for a perfect Bayesian equilibrium. Furthermore, I focus on the equilibria favored by the DM; that is, those with the maximum number of high-quality entrants.
Information overload As would be expected, when the cost of entry decreases, the supply of experts – and hence the number of actions from which the DM can choose – increases. However, as the DM's choice set grows, her expected utility first increases, but then decreases. Proposition 2 states this key result.
Proposition 2 (information overload)
As qS → 0, the DM receives more cues, but eventually processes fewer. Her expected utility first increases and then decreases.
It is instructive to describe how equilibrium behavior in the selection stage changes as the cost of sending cues, q S, falls from prohibitively large to negligibly small. The impact on the DM's expected utility is illustrated in Figure 2, where a decrease in q S represents a movement from right to left on the x-axis.
• For high enough q S, cues are so expensive that no expert enters.
• As q S falls, it at some point becomes sufficiently attractive for some high-quality experts to enter. Here, the cues in themselves are signals of high quality, so the DM need not process them, but can select her communication partner(s) for the deliberation stage at random from the pool of entrants. (This relies on the assumption that the DM can observe that a cue was sent even if she does not assimilate it. If we relax this, the economic insights remain valid, as I explain below.) In this signaling outcome, the DM's welfare increases as q S falls so long as the number of entrants is smaller than two – or, more generally, smaller than the number of experts with whom she can communicate in the deliberation stage; otherwise, the DM's welfare remains constant. This is captured in Figure 2: as q S decreases, the DM benefits from an expansion in information supply so long as
 $q_S \gt \overline {q_S} $. Then, as q S falls further (but remains above qS), the DM has access to (at least) two high-quality experts, but no low-quality experts, so her expected utility remains flat as q S falls further.
$q_S \gt \overline {q_S} $. Then, as q S falls further (but remains above qS), the DM has access to (at least) two high-quality experts, but no low-quality experts, so her expected utility remains flat as q S falls further.• As q S falls below qS, some low-quality experts find it attractive to enter as well. A signaling equilibrium, in which a random pick from among the entrants ensures a high-quality expert for the deliberation stage, no longer exists. The DM reacts in one of two ways: either she continues to randomize and simply accepts the lower (average) expert quality or, if q R is not too high, she reads cues with positive probability to screen out low-quality experts. So as not to make the selection stage trivial, I focus on q R that is low enough for the DM to engage in active screening. Clearly, her welfare decreases as q S falls, as it becomes harder to spot high quality. Already, the arrival of more cues – essentially, access to more information – makes the DM worse off. The next stage is merely the copestone.
• As q S vanishes, the avalanche of low-quality cues reduces the average quality in the entrant pool so much that screening becomes futile – high quality becomes the proverbial needle in the haystack. As a result, there is neither signaling nor screening, just pooling: the DM gives up on active selection and accepts that she is all but bound to encounter low quality in the deliberation stage. Her expected utility thus approaches U*, her expected utility from communicating with two low-quality experts (on two low-quality actions) in the deliberation stage.
Thus, at a certain point, as the competition for the DM's attention increases and she gets more information, she processes less of it – or tunes out – and fares worse. I refer to this phenomenon – the more cues the DM gets, the fewer she processes and the worse she fares – as information overload.Footnote 12
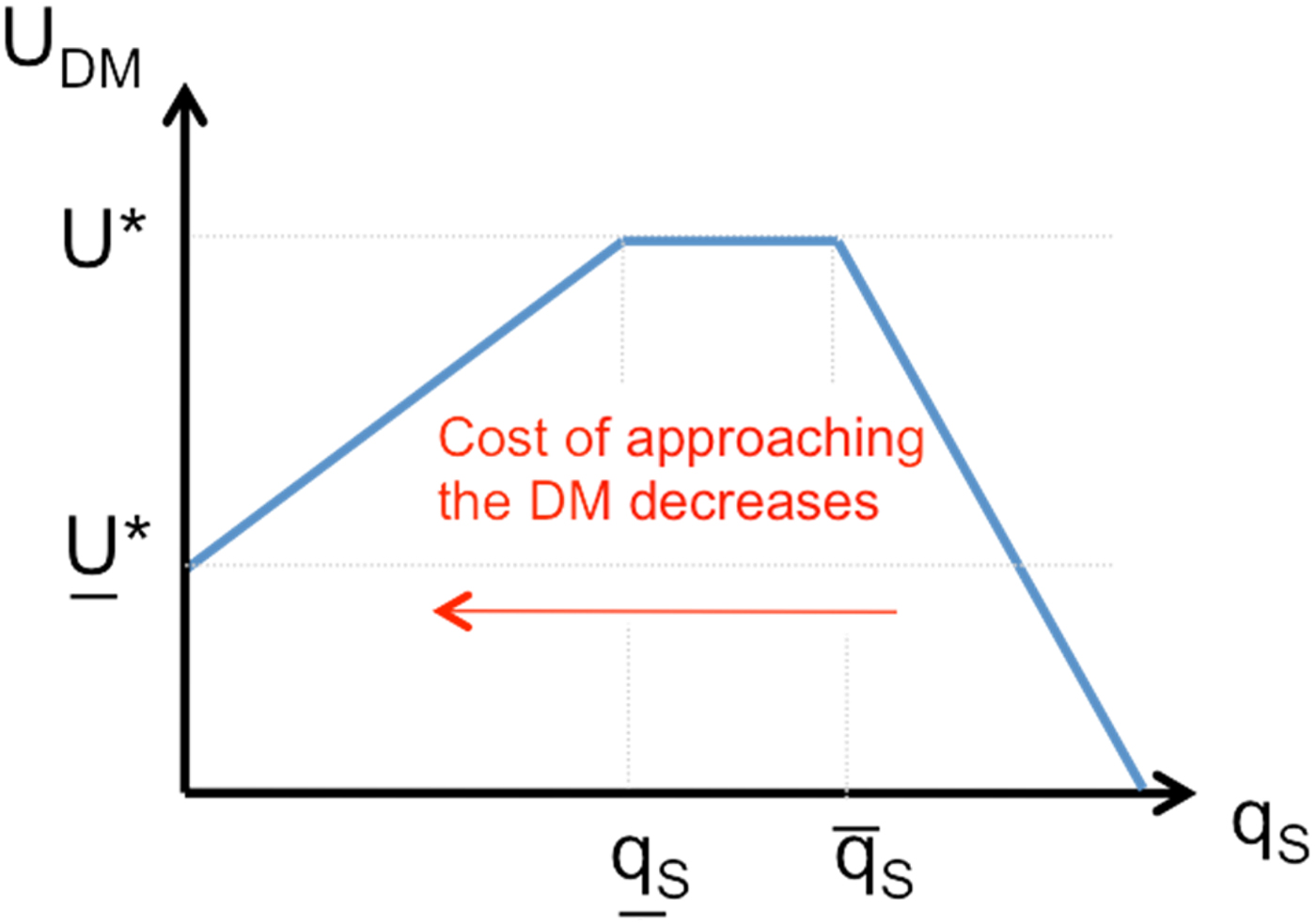
Figure 2. Information overload. A movement from right to left on the x-axis represents a decrease in the cost of entry, q S. As q S decreases, the DM first benefits from an expansion in information supply (so long as ![]() $q_S \gt \overline {q_S} $). Then the DM has access to (at least) two high-quality experts, but no low-quality experts, so she obtains her maximum possible (decision) payoff, U*. As the cost of entry falls below qS, low-quality experts join the battle for access to the DM's attention and her expected utility falls below U*. When q S → 0, the number of low-quality experts who enter tends to infinity, so the DM ceases to screen experts. Her decision payoff falls, as she relies on information of lower quality on average. Thus, when information becomes cheap enough, the more information she gets, the less information she processes and the worse she fares.
$q_S \gt \overline {q_S} $). Then the DM has access to (at least) two high-quality experts, but no low-quality experts, so she obtains her maximum possible (decision) payoff, U*. As the cost of entry falls below qS, low-quality experts join the battle for access to the DM's attention and her expected utility falls below U*. When q S → 0, the number of low-quality experts who enter tends to infinity, so the DM ceases to screen experts. Her decision payoff falls, as she relies on information of lower quality on average. Thus, when information becomes cheap enough, the more information she gets, the less information she processes and the worse she fares.
It is instructive to make precise how (the idea of) information overload is related to (the idea of) limited attention. To this end, consider this quote by Simon (Reference Simon and Greenberger1971: 40–41):
What information consumes is rather obvious: it consumes the attention of its recipients. Hence a wealth of information creates a poverty of attention, and a need to allocate that attention efficiently among the overabundance of information sources that might consume it.
Thus, attention, in limited supply, becomes a scarcer resource in relative terms when confronted with more information. But this does not imply information overload or that more information provided can decrease knowledge acquired. The idea of information overload is that a wealth of information not only “creates … a need to allocate that attention” (emphasis added), but actually impairs the ability to do so efficiently.
Alternative assumptions If I instead assume that the DM cannot observe that a cue was sent unless she incurs a cost to read it, the economic insights remain: she must open exactly two cues so long as only high-quality experts enter; then, she must either open exactly two cues but rely on information of lower quality or open more than two cues on average to identify two high-quality experts. In either case, her expected utility remains constant when only high-quality types enter and decreases with the number of low-quality types.
Further, the equilibria described above exist even if we relax the assumption that an expert must send a cue to enter. However, in that case, there is a further equilibrium for q S → 0 in which the experts cease to send cues, aware that they are no longer processed, and the DM picks randomly from the entire pool of experts. Still, the DM favors the equilibrium in which she picks randomly from a subset of experts – which includes all high-quality experts – who send a cue, because it offers better odds of picking a high-quality expert.
Also, we need not assume differences in quality. Instead, suppose experts invest in quality. Specifically, suppose all N experts begin with low quality (α = α), but can invest in high quality ![]() $\left( {{\rm \alpha} = \bar {\rm \alpha}} \right)$ at some cost c > 0 before entering. Proposition 2 implies that information overload frustrates investment in high quality. Intuitively, the value of quality is reflected in the expected utility difference between a high-quality and a low-quality type. For prohibitive q S, both types expect to earn zero, so there is no incentive to invest in quality. As q S falls, if c is not too high, some invest in quality and send cues. But as q S → 0, information overload erodes the premium on quality, so again no one invests. The supply of high quality collapses when it becomes too cheap to approach the DM. This is not because the DM ceases to value quality. On the contrary, she would like to treat high-quality experts preferentially; however, she in unable to do so when finding them amounts to looking for a needle in a haystack.
$\left( {{\rm \alpha} = \bar {\rm \alpha}} \right)$ at some cost c > 0 before entering. Proposition 2 implies that information overload frustrates investment in high quality. Intuitively, the value of quality is reflected in the expected utility difference between a high-quality and a low-quality type. For prohibitive q S, both types expect to earn zero, so there is no incentive to invest in quality. As q S falls, if c is not too high, some invest in quality and send cues. But as q S → 0, information overload erodes the premium on quality, so again no one invests. The supply of high quality collapses when it becomes too cheap to approach the DM. This is not because the DM ceases to value quality. On the contrary, she would like to treat high-quality experts preferentially; however, she in unable to do so when finding them amounts to looking for a needle in a haystack.
Externalities as the driving force of information overload The immediate cause of information overload is that the quality of proposed actions decreases with the quantity; actions worthy of deliberation become the proverbial needle in a haystack. The deeper cause, though, is negative externalities: entry is individually rational for each expert, even as it complicates the selection problem for the DM and spoils overall communication. This is because each expert ignores how his own entry affects the communication environment as a whole. If the expert were identical for all actions, he would send cues only for two high-quality actions. In the decentralized setting, however, sending cues remains individually rational even as each cue sent aggravates the complexity of the DM's selection problem up to a point where active selection breaks down. This, in turn, frustrates the incentives to produce quality. Intuitively, it is as if the low-quality experts, each seeking to be noticed, pollute the DM's attention field. Indeed, information overload is similar to pollution or congestion and, like them, may be amenable to efficiency-improving intervention. The next subsection addresses practical expressions of information overload and discusses the fact that a DM with limited attention may want to limit access to her attention space, even if that reduces her choice set. In a nutshell, she faces a trade-off between comprehensiveness and comprehensibility.
Information overload in practice
With recent advances in information technology, individuals face massive data via more channels (phone, Internet, email, instant messages, etc.) and on more platforms (Facebook, Twitter, blogs, etc.). In the presence of information overload, such an abundance of information can be counterproductive. Indeed, a business research firm nominated information overload as the ‘problem of the year’ in 2008, predicting that it would cost firms US$650 billion in lost productivity and innovation due to ‘unnecessary interruptions’. The main concern is that an escalating quantity of information comes with a decline in average quality and that this inverse relationship between amount and relevance makes it harder to find ‘good’ information.Footnote 13 This makes selection, as in my model, a daunting issue and suggests that consumers should value products that help reduce their choice sets and improve selection.
In this vein, several technology firms, including Microsoft, Intel, Google and IBM, recently formed a nonprofit organization, the Information Overload Research Group, to develop solutions to information overload.Footnote 14 Google's success formula, its ranking algorithm, implements pre-selection. And its ubiquity on the Internet, as gateway and gatekeeper, betrays the import of information overload. The logic of pre-selection also underlies solutions such as email filters, ranking inbox messages by imputed importance, compiling communication histories for every sender, displaying email portions to allow for fast screening and sophisticated filing and search functions. Such ranking of electronic messages minimizes information overload; that is, it reduces the “economic loss associated with the examination of a number of non- or less-relevant messages” and distinguishes “communications that are probably of interest from those that probably aren't” (Losee, Reference Losee1998).
Information overload is not just a matter of Internet and emails. In a seminal study, Jacoby et al. (Reference Jacoby, Speller and Kohn Berning1974) explored how the quality of consumption decisions depends on ‘information load’, measured as the number of brands as well as the amount of information per brand provided. Their experiment showed that the ability to pick the best product dropped off at high levels of information load. In Jacoby et al. (Reference Jacoby, Kohn Berning and Speller1973), a companion paper, they further showed that the subjects spent less time on processing information – or, in their words, ‘tuned out’ – once the information load exceeded a certain threshold.Footnote 15 Many other experiments in organization science, accounting, marketing and information science corroborate the notion that more information can impair cognitive processes and decisions (Edmunds & Morris, Reference Edmunds and Morris2000; Eppler & Mengis, Reference Eppler and Mengis2004).
Because information overload is a driving force behind innovations in communication and information management, it is connected to recent research on choice architecture; that is, how the presentation of choices affects decisions (Thaler & Sunstein, Reference Thaler and Sunstein2008). Cronqvist and Thaler (Reference Cronqvist and Thaler2004), for example, studied the introduction of a new retirement savings plan in Sweden in 1993. Eligible Swedes were encouraged to choose five out of 456 funds, to which their savings would be allocated. A third of all eligibles made no active choices; their savings were instead allocated to a default fund (essentially a pre-selection by the government). Information overload seems a likely reason that so many Swedes relied on the default choice: comparing hundreds of funds is a Herculean task for ordinary households, and one might expect many of them to resort to the default or make superficial active decisions. Indeed, studying the same Swedish reform, Karlsson et al. (Reference Karlsson, Massa and Simonov2006) showed that funds that (for exogenous reasons) were better represented in the fund catalogue – that is, had better ‘menu exposure’ – received more active contributions.Footnote 16
All of the above examples suggest that DMs can benefit from receiving less information, despite the associated decrease in choice set. Indeed, in the presence of information overload, there is a trade-off between variety and simplicity, or between comprehensiveness and comprehensibility. This evidence contrasts with models of decision-making under unlimited attention, where a larger choice set cannot make an individual worse off.
A single expert and strategic attention manipulation
In the previous section, we saw that crowding out and information overload result from the strategic interaction between multiple experts, each of whom try to persuade the DM to take one distinct action. By making minor modifications to the original setting, this section reinterprets the framework to study a DM who communicates with a single expert on one action that has several aspects. In the deliberation stage, the DM's multi-tasking problem now stems from the fact that the DM must decide how to allocate her scarce attention between the various aspects of the action. In the selection stage, recall that in the ‘multiple experts’ setting analyzed in the previous section, the DM is unsure of each action's ex ante appeal. The analogue in this section is that the DM is unsure which aspects of the (single) action are financially relevant and hence worth devoting attention to in the deliberation stage. Next, we introduce the setup in detail.
Modified setup: deliberation and selection stages
The DM communicates with a single expert about one action, A, which has many aspects. Specifically, suppose the DM's payoff from A can be expressed as the sum of N R components: ![]() $\tilde x = \mathop \sum \nolimits_1^{N_R} \tilde x_i $. Each component takes the value
$\tilde x = \mathop \sum \nolimits_1^{N_R} \tilde x_i $. Each component takes the value ![]() $\bar x \gt 0$ with probability α i and otherwise the value x < 0. So the expected payoff from A is
$\bar x \gt 0$ with probability α i and otherwise the value x < 0. So the expected payoff from A is ![]() $E\left( {\tilde x} \right) = N_R \left[ {\bar \alpha \bar x + \left( {1 - \bar \alpha} \right)\underline{x}} \right]$, where
$E\left( {\tilde x} \right) = N_R \left[ {\bar \alpha \bar x + \left( {1 - \bar \alpha} \right)\underline{x}} \right]$, where ![]() $\bar \alpha = \displaystyle{(1 / {N_R})} \mathop \sum \nolimits_1^{N_R} \alpha _i $. Similar to before, absent more information, the DM takes A in the deliberation stage if and only if
$\bar \alpha = \displaystyle{(1 / {N_R})} \mathop \sum \nolimits_1^{N_R} \alpha _i $. Similar to before, absent more information, the DM takes A in the deliberation stage if and only if ![]() $\bar \alpha \gt \alpha ^{\rm *} \equiv \displaystyle{{ - \underline{x}} / ({\bar x - \underline{x}})} $. Or, put differently, if the DM can obtain more information, she uses an opt-in rule if
$\bar \alpha \gt \alpha ^{\rm *} \equiv \displaystyle{{ - \underline{x}} / ({\bar x - \underline{x}})} $. Or, put differently, if the DM can obtain more information, she uses an opt-in rule if ![]() $\bar \alpha \; $≤ α* and an opt-out rule if
$\bar \alpha \; $≤ α* and an opt-out rule if ![]() $\bar \alpha$ > α*.
$\bar \alpha$ > α*.
In addition to the N R components of the action A that are relevant to the action's payoff, there exist additional ![]() $N_\emptyset $ components of A that are irrelevant to the DM's payoff. I assume that the DM does not know which components are relevantFootnote 17 and is potentially unaware of components per se. Intuitively, this captures a plausible situation: inclined toward a particular choice, the DM might yet discover (financially relevant) aspects that change her opinion. Thus, the DM is faced with two sets of questions: what components exist and which ones are relevant (selection stage)? And how much attention should a given component receive (deliberation stage)?
$N_\emptyset $ components of A that are irrelevant to the DM's payoff. I assume that the DM does not know which components are relevantFootnote 17 and is potentially unaware of components per se. Intuitively, this captures a plausible situation: inclined toward a particular choice, the DM might yet discover (financially relevant) aspects that change her opinion. Thus, the DM is faced with two sets of questions: what components exist and which ones are relevant (selection stage)? And how much attention should a given component receive (deliberation stage)?
As before, the expert's communication incentives hinge on the DM's decision rule: if the DM follows an opt-in rule, the expert must persuade her to take the action. To maximize the chances that the DM revises her beliefs upward and so opts in, the expert seeks to draw her attention to those aspects that are most likely to yield favorable information; that is, he sends her cues about, and exerts persuasion effort on, the topics with the highest α i.
By contrast, if the DM follows an opt-out rule, her default is to take action A, but she may depart from this default – and opt out – if she learns about any relevant aspects of the action that are unfavorable. Then, the expert wants to withhold the relevant information. In the model, this means that, on his own accord, he would never send a cue about any relevant aspect in the selection stage, since this could only induce the DM to devote attention to it in the deliberation stage and subsequently to change her mind and abandon the action after all. In this situation, a mandatory disclosure law would make a difference to the expert's communication strategy: by mandating that the expert (firm) reveals any relevant financial aspects of the product, it would be illegal to withhold this information.
To formalize what happens when the expert is subjected to such a mandate, assume for simplicity that there is one relevant topic, N R = 1, that the number of irrelevant topics ![]() $N_\emptyset $ is infinite and that the DM can at most deliberate on two topics (as in the previous section). These assumptions are merely simplifying; indeed, the ‘strategic information overload’ result reported below holds as long as the DM can devote attention to only a limited number of topics in the deliberation stage and
$N_\emptyset $ is infinite and that the DM can at most deliberate on two topics (as in the previous section). These assumptions are merely simplifying; indeed, the ‘strategic information overload’ result reported below holds as long as the DM can devote attention to only a limited number of topics in the deliberation stage and ![]() $N_\emptyset $ is sufficiently large relative to N R. Finally, as before, it is costly for the DM to process cues: q R >0. For convenience, I refer to cues about relevant (irrelevant) topics as relevant (irrelevant) cues.
$N_\emptyset $ is sufficiently large relative to N R. Finally, as before, it is costly for the DM to process cues: q R >0. For convenience, I refer to cues about relevant (irrelevant) topics as relevant (irrelevant) cues.
Strategic information overload and the limitations of mandatory disclosure laws
When ![]() $\bar \alpha \gt \alpha ^{\rm *} $, the DM follows an opt-out rule. Thus, if the DM lacks access to – or is unaware of – the relevant topic, the expert has no reason to bring it to her attention by sending a relevant cue. In fact, the expert is best off sending no cues at all. Now suppose that, by a disclosure mandate, the relevant cue must be sent.
$\bar \alpha \gt \alpha ^{\rm *} $, the DM follows an opt-out rule. Thus, if the DM lacks access to – or is unaware of – the relevant topic, the expert has no reason to bring it to her attention by sending a relevant cue. In fact, the expert is best off sending no cues at all. Now suppose that, by a disclosure mandate, the relevant cue must be sent.
Proposition 3 (strategic information overload)
Let ![]() $\bar \alpha \gt \alpha ^{\rm *} $. Suppose that disclosure laws mandate that the relevant cue is sent. As q S → 0, the expert sends an increasing swarm of irrelevant cues and the DM's expected utility decreases.
$\bar \alpha \gt \alpha ^{\rm *} $. Suppose that disclosure laws mandate that the relevant cue is sent. As q S → 0, the expert sends an increasing swarm of irrelevant cues and the DM's expected utility decreases.
Proposition 3 is closely related to the information overload result in the previous section, yet the underlying economic mechanism is different. In the previous section, information overload resulted from various experts’ competition for attention. Proposition 3 shows that a single expert, who faces no competition for the DM's attention but who can communicate with the DM about multiple aspects of the action for which he advocates, strategically induces information overload in the DM when he is subjected to a disclosure provision that mandates drawing the DM's attention to the financially relevant aspect of the action (the product he tries to persuade the DM to buy).
Intuitively, the expert is afraid that the DM, by paying attention to the relevant topic, might discover unfavorable information about the action and opt out. To reduce the odds that the DM identifies – that is, selects – the relevant topic, the disclosure mandate thus gives the expert an incentive to supply irrelevant aspects in the selection stage by sending out irrelevant cues, even though this is costly for him. A swarm of mostly irrelevant cues, in turn, thwarts the DM's chances, and hence her incentives, to pinpoint the relevant topic. In other words, the expert intentionally induces information overload, which effectively conceals the inconvenient aspect that the firm was mandated to disclose in the first place. In a nutshell, the disclosure mandate, which is intended to raise the DM's awareness of the financially relevant aspect of the product that she considers, generates a response on the part of the expert that in practice renders the DM financially illiterate, or obfuscates her.
As a result, the disclosure mandate has no impact on the DM's final decision; she buys the product even if an understanding of the financially relevant aspect would have pushed her to opt out, since strategic information overload makes her as uninformed in the presence of a mandate as she is in its absence. This sharply illustrates that, when consumers’ attention is limited, simple disclosure rules can be completely impotent and have no impact on social welfare.
Strategic information overload in practice USA Today recently ran an internal study on the costs of maintaining a basic checking account at the ten largest US banks and credit unions. While the most basic fees were found to be disclosed on the institutions’ websites, many others were listed only in the ‘Schedule of Fees and Charges’. That, however, turned out to be difficult to find.
But even the world's largest search engine couldn't unearth a fee schedule for HSBC, TD Bank, Citibank and Capital One. To get their fee information, we had to e-mail or call the banks.
Determined customers can search for information about fees in banks’ official disclosure documents, but they'll need a lot of time and a couple of cups of coffee, too. An analysis of checking accounts for the 10 largest banks by the Pew Health Group found that the median length of their disclosure statements was 111 pages. None of the banks provided key information about fees on a single page…Footnote 18
Note that the issue was not only that the ‘inconvenient’ information was at times unavailable, it was also that, even when provided, it was made available in a way that made it costly to locate the relevant information; that is, in a way that induced strategic information overload in the customer. Ordinary customers would be hard-pressed to know not only where to look for relevant items, but also what items to look for. Similar conditions prevail in other countries. In 2008, the website This Is Money cited a warning by the British consumer and competition authority, the Office of Fair Trading, that:
[credit card] providers can add to the problem knowing that consumers cannot process complex information … They can create ‘noise’ by increasing the quantity and complexity of information, which makes it difficult for consumers to see the real price.Footnote 19
Note that the concern here is the complexity of information; even if a product itself is simple, information overload effectively presents it in an overly complex fashion by hiding it in very long disclosure statements. The financial products market seems rife with such practices.Footnote 20 Credit cards are perhaps the most widely debated example. As quoted in a 2009 Reuters article, President Obama said, “No more fine print, no more confusing terms and conditions,” in a meeting with US credit card company executives on consumer protection regulation.Footnote 21
These examples underscore an interesting aspect that eludes many communication models: mandatory disclosure is not a panacea. In the above examples, the communication problem is neither a willful misrepresentation (‘cheap talk’) nor the withholding of facts (‘strategic non-disclosure’). Here, the banks are mandated to provide fee information; cheap talk and non-disclosure are illegal and would have serious consequences ex post. Still, this does not mean that consumers become well-informed. Even when information is hard and disclosed, senders can still – through strategic attention manipulation – conceal what is relevant by manipulating the sheer amount of information. Thus, simple disclosure rules like the Truth in Lending Act may prove completely ineffective when consumers’ attention is limited.Footnote 22
Complexification and the limitations of ‘simple labels’ for consumer protection
The previous subsection illustrates that too much disclosure can be as concerning as too little; a surfeit of details can prove as uninformative as a dearth thereof. But if disclosure mandates can backfire because firms can induce information overload, intuition suggests an immediate solution: to mandate not only what firms disclose, but also that it is disclosed in an easy-to-understand way. Indeed, more recent disclosure rules often are of this flavor: credit card companies must now disclose key details of the products they offer in a salient fashion, health insurance companies must provide a Summary of Benefits and Coverage of each plan offered and food producers must adhere to standardized labeling regulations to declare all ingredients and the caloric content of each serving, for example.
In this subsection, I use the theoretical framework to analyze the strategic response on the part of an expert (firm) when faced with a mandate to provide easy-to-understand information about the product it sells. As we will see, even detailed mandates to disclose easy-to-understand information can backfire by inducing a ‘complexification’ of the underlying product itself. I show this by extending the model with a single expert to allow the DM's payoff from the (single) action to be composed of many components and to allow the expert to manipulate that composition so long as the total payoff stays constant. Intuitively, such payoff-equivalent variations amount to changing the number of financially relevant aspects of the product. Below, I formalize this.
To allow for complexification, I introduce an option enabling the expert to design A in a way that makes its payoff less transparent. As before, the DM's payoff is – at least initially – the sum of N R components, ![]() $\tilde x = \mathop \sum \nolimits_1^{N_R} \tilde x_i $, and each component takes the value
$\tilde x = \mathop \sum \nolimits_1^{N_R} \tilde x_i $, and each component takes the value ![]() $\bar x$ > 0 with probability α i and otherwise the value x < 0. However, the expert can now recompose the payoff structure into any form
$\bar x$ > 0 with probability α i and otherwise the value x < 0. However, the expert can now recompose the payoff structure into any form ![]() $\tilde y = \mathop \sum \nolimits_1^N \tilde y_J $, so long as the total (realized) payoff is invariant:
$\tilde y = \mathop \sum \nolimits_1^N \tilde y_J $, so long as the total (realized) payoff is invariant: ![]() $\tilde y = \tilde x$. I call
$\tilde y = \tilde x$. I call ![]() $\tilde y$ a payoff-equivalent variation (of
$\tilde y$ a payoff-equivalent variation (of ![]() $\tilde x$). Crucially, I assume that the DM does not know the ‘original’ composition,
$\tilde x$). Crucially, I assume that the DM does not know the ‘original’ composition, ![]() $\left\{ {\tilde x_i} \right\}$.Footnote 23 In any case, absent communication, such variation does not matter; it affects neither the DM's decision nor her welfare.
$\left\{ {\tilde x_i} \right\}$.Footnote 23 In any case, absent communication, such variation does not matter; it affects neither the DM's decision nor her welfare.
As an illustration, consider two simple mathematical operations the expert can use to create payoff-equivalent variations. One is to divide each ![]() $\tilde x_i $ into m parts,
$\tilde x_i $ into m parts, ![]() $\mathop \sum \nolimits_{h = 1}^m \tilde x_{ih} = \tilde x_i $, so that the new payoff structure has N = mN R components:
$\mathop \sum \nolimits_{h = 1}^m \tilde x_{ih} = \tilde x_i $, so that the new payoff structure has N = mN R components: ![]() $\tilde y = \mathop \sum \nolimits_{i = 1}^{N_R} \mathop \sum \nolimits_{h = 1}^m \tilde x_{ih} = \mathop \sum \nolimits_{j = 1}^N \tilde y_j $. For example, instead of incorporating total expenses into one salient item, such as the monthly rent, a landlord might disaggregate them into various fees, such as for maintenance, utilities, move-in or move-out, parking, laundry room or other administrative services. The other operation is to add components that neutralize each other, as in
$\tilde y = \mathop \sum \nolimits_{i = 1}^{N_R} \mathop \sum \nolimits_{h = 1}^m \tilde x_{ih} = \mathop \sum \nolimits_{j = 1}^N \tilde y_j $. For example, instead of incorporating total expenses into one salient item, such as the monthly rent, a landlord might disaggregate them into various fees, such as for maintenance, utilities, move-in or move-out, parking, laundry room or other administrative services. The other operation is to add components that neutralize each other, as in ![]() $\tilde y = \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i + \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i - \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i = \mathop \sum \nolimits_{j = 1}^N \tilde y_j $, where N = 3N R. A real-world example is a purchase involving a nominal price, fees, taxes, discounts, bonuses, rewards and so forth that partly offset each other. In both examples, seeing one component is not informative about the others.
$\tilde y = \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i + \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i - \mathop \sum \nolimits_{i = 1}^{N_R} \tilde x_i = \mathop \sum \nolimits_{j = 1}^N \tilde y_j $, where N = 3N R. A real-world example is a purchase involving a nominal price, fees, taxes, discounts, bonuses, rewards and so forth that partly offset each other. In both examples, seeing one component is not informative about the others.
Even if the total expected payoff remains unchanged, the payoff composition matters for communication. As before, suppose the DM cannot deliberate on more than a certain number of topics (in keeping with the previous framework, say, two). A proliferation of components then causes more relevant information to slip her attention. Furthermore, disaggregating the payoff can make each component, in and of itself, less important. To see this point, let ![]() $\tilde x_{ih} = \displaystyle{{\tilde x_i} / m}$ for all i in the first (landlord) example above. Increasing m leaves the total payoff
$\tilde x_{ih} = \displaystyle{{\tilde x_i} / m}$ for all i in the first (landlord) example above. Increasing m leaves the total payoff ![]() $\tilde y$ unchanged, but shrinks every component
$\tilde y$ unchanged, but shrinks every component ![]() $\displaystyle{{\tilde x_i} / m}$. Crucially, this reduces how much the DM can learn from a given number of components.
$\displaystyle{{\tilde x_i} / m}$. Crucially, this reduces how much the DM can learn from a given number of components.
Payoff-equivalent variation is thus a means of manipulating the DM's learning process. How the expert uses such means hinges, as before, on the DM's decision rule. If she uses an opt-in rule, the expert wants to help her learn more about A. He would set N ≤ 2 – such that no relevant aspect escapes deliberation – and exert communication effort on all the components; that is, he would simplify the payoff structure and strive to explain.
By contrast, if the DM follows an opt-out rule, the expert wants to do the exact opposite. He would increase the number of components, even if it were costly to do so, only to thwart learning. Suppose he must pay v > 0 to raise N by one.
Proposition 4 (complexification)
Let ![]() $\bar \alpha \gt \alpha ^{\rm *} $. Suppose all relevant cues are sent out. As v → 0, the expert sets N → +∞, and the DM's expected utility falls to
$\bar \alpha \gt \alpha ^{\rm *} $. Suppose all relevant cues are sent out. As v → 0, the expert sets N → +∞, and the DM's expected utility falls to ![]() $E\left( {\tilde x} \right)$.
$E\left( {\tilde x} \right)$.
As v → 0, the expert increases N such that more relevant information escapes the DM's attention, given that she can deliberate on only a limited number of components. At the same time, he disaggregates the payoff to reduce the amount of information she can possibly wrest from any given component. In the limit, even what she can learn from the components she is capable of studying becomes so trivial that it no longer affects her decision: she chooses what she would have chosen without the information. Intuitively, the expert makes the action unnecessarily complex and thereby successfully prevents the DM from getting the full picture.
Complexification thus has the same welfare consequences as inducing information overload – it can eradicate all intended welfare gains from mandated information provision, even if the mandate prohibits unclear communication.
Complexification in practice According to Edward L. Yingling, president and chief executive of the American Bankers Association (ABA), during his first term, President Obama urged credit card companies “to issue a simple credit card product” (emphasis added). A year earlier, after similar comments by Federal Reserve Chairman Ben S. Bernanke “that improved disclosures alone cannot solve all of the problems consumers face in trying to manage their credit card accounts,” the ABA and other industry representatives had signaled strong opposition to such interventions.Footnote 24
The UK financial regulator, the Financial Services Authority, is also quoted as saying:
[P]roviders of financial products may gain from the lack of price transparency about their products … It may be in the provider's interest to increase the complexity of the product charges.
Other examples of complexification come from the food industry, where legislation mandates that all ingredients be listed in a food declaration; however, ‘incidental additives’ need not be listed. This has provided food producers with incentives for complexification, most prominently by removing an ingredient that consumers may want to avoid and replacing it with one or several incidental additives that accomplish the same effect in food but that remain invisible (provided each of them is included in small enough a quantity). A recent example is Starbuck's use of a color additive derived from the animal world classified as an incidental additive instead of an ingredient, which effectively caused a non-vegan product to be labeled vegan, leading to a stir among vegan consumers.Footnote 25 Similarly, widespread consumer awareness of the dangers of bisphenol-A (BPA) has spurred the development of a new range of plastic products labeled ‘BPA free’; however, these products contain BPA replacement substances that allegedly have produced health problems similar to those associated with BPA itself.Footnote 26 Clearly, in the absence of mandated disclosure of the ingredients in food, none of these complexifications was necessary; in the presence of this disclosure rule, however, they represented strategic responses on the part of food producers.Footnote 27
As opposed to the examples presented in the previous subsection, which showed manipulation of the complexity of information, the examples provided here refer to manipulation of the complexity of the product itself. Whether the complexity of information or the complexity of the product itself is involved, the danger is that misguided decisions affect consumers’ risk of getting into debt or of buying food products that they wish to avoid.
However, while complexity of information has a simple legislative recipe mandating that firms provide easy-to-understand information, complexification is much harder to address from a legislative perspective. In fact, Proposition 4, along with the real-world examples of complexification presented in this subsection, underscore that even the most elaborate disclosure rule – which specifies exactly how easy-to- understand information should be provided – may be completely ineffective for the consumer. This is because any regulation at the communication level proves futile if the seller can modify the object of communication in a way that makes it intellectually challenging to grasp, even with all details correctly disclosed. While the communication is correct, the matter to be decided becomes too complicated. In such a case, to be effective, regulation may have to target the object of communication per se; that is, product design. This, as the examples illustrate, is a much thornier issue.
Conclusion
Limits on consumer attention give firms incentives to manipulate prospective buyers’ allocation of their attention. In the presence of attention manipulation, competitive information supply can reduce consumer knowledge by causing information overload. Moreover, a single firm subjected to a disclosure mandate may deliberately induce information overload to obfuscate financially relevant information or engage in product complexification to bound consumer financial literacy.
These findings demonstrate that attention limitations matter crucially for whether disclosure regulation improves consumer welfare: disclosure rules that would improve welfare for agents without attention limitations can prove ineffective for consumers with limited attention. Obfuscation suggests a role for rules that mandate not only the content, but also the format of disclosure; however, even rules that mandate disclosure of ‘easy-to-understand’ information are ineffective against complexification, which may call for regulation of product design.
An interesting avenue not pursued in the present paper is that heterogeneity in attention constraints may provoke multiple forms or degrees of attention manipulation. Banerjee and Mullainathan (Reference Banerjee and Mullainathan2008) posited that the poor are subject to tighter attention constraints than the rich, who can afford better technologies to free up attention. They then showed that this induces differences in productivity that amplify the differences in initial endowment; inequality breeds more inequality. Allcott and Taubinsky (Reference Allcott and Taubinsky2015) and Taubinsky and Rees-Jones (Reference Taubinsky and Rees-Jones2015) similarly documented considerable heterogeneity in attention limitations, and Taubinsky and Rees-Jones (Reference Taubinsky and Rees-Jones2015) showed that lower-income individuals have more severe attention limitations. The current paper's findings suggest that the problem may be even worse: the poor may not only start out with tighter attention constraints, but may also find their limited attention exploited more than the rich. In short, the tighter constraints may make them less productive and more manipulable. Manipulation is perhaps the more worrisome problem in that it is, as shown in this paper, prone to create externalities and thus constrained, inefficient outcomes. But such questions are left for future research.
Supplementary Material
To view supplementary material for this article, please visit https://doi.org/10.1017/bpp.2017.10.
Acknowledgements
I am grateful to Navin Kartik, Doug Bernheim, Patrick Bolton, Yeon-Koo Che, Pierre-André Chiappori, Matt Gentzkow, Takakazu Honryo, Samuel Lee, Uliana Loginova, Florian Scheuer and Cass Sunstein and to seminar participants at the Consumer Financial Protection Bureau and at various universities. I also thank the faculty and participants of the Russell Sage Foundation Summer Institute in Behavioral Economics.




