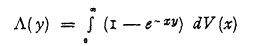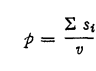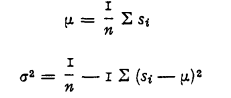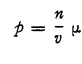The paper considers the problem of finding an upper bound for the Stop loss premium.
We will start with a brief sketch of the practical context in which this problem is relevant.
If it is reasonable to assume, that the accumulated claims variable of the underlying risk can be represented by a Compound Poisson Process, the following data are needed for fixing the Stop loss premium:
— the claims intensity,
— the distribution of the claimsizes (jump-size variable).
In practical situations it is usually possible to find a reasonable estimate for the claims intensity (expected number of claims in a given period).
Generally speaking, however, it is not so easy to get sufficient data on the claimsize distribution. Ordinarily only its mean is known. This deficiency in information can of course be offset by assuming the unknown distribution to be one of the familiar types, such as Exponential, Gamma or Pareto.
Stop loss premiums are however very sensitive to variations in the type of claimsize distribution and consequently it can make a lot of difference in the result what particular choice is made.
To gain some insight into the consequences of a specific assumption, it is useful to know within what range the premium can move for varying distributional suppositions. This means establishing an upper bound and a lower bound. The lower bound is trivially obtained if the mass of the claimsize distribution is solely concentrated at its mean. The upper bound on the other hand should correspond to the “worst” possible claimsize distribution. This means, that we have to look for a distribution which maximizes the Stop loss premium.