In the classical definition skewness is departure from symmetry. It was therefore natural to measure skewness by using a normalized third moment μ3/σ3. This condensed measure, however, is not refined enough to be used as an operational instrument for studying various functions which might be used to describe actual claim distributions. This is true especially when the interest is concentrated towards the higher values of the variate.

In their paper (1) Benktander-Segerdahl have suggested that the average excess claim m(x) as a function of the priority x should be used to reveal the characteristics of the tail of the distribution

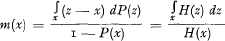
where P(x) = 1 — H(x) denotes the distribution function.

This statistic is very apt when comparing actual claim distributions with possible theoretical models. It is also useful when classifying these models.

If, however, emphasis mainly is laid on classifying distributions according to their skewness, another statistic might be preferable. Let μ(x)dx denote the probability that a stochastic variable which is known to be at least equal to x, does not exceed x+dx. In other words, μ(x)dx represents the probability that a claim or the corresponding stochastic variable, which, when observed from the bottom, is “alive” at x, “dies” in the interval (x, x + dx). The lower this claims rate of mortality, the skewer and more dangerous is the claim distribution.