On sait que la loi de Poisson simple représente mal la distribution des sinistres d'un groupe observé d'automobilistes du fait que tout groupe que l'on peut étudier en pratique, même s'il est composé d'assurés présentant des caractéristiques communes (même zone de circulation, même type de véhicule, même utilisation de ce véhicule, …) est hétérogéne quant aux autres caractéristiques et surtout quant au comportement personnel des assurés, élément dont l'influence sur les résultats du risque est prépondérante.

M. Delaporte a obtenu une représentation intéressante du phénomène en supposant que les sinistres d'un véhicule se répartis-sent suivant une loi de Poisson de moyenne donnée, et que les moyennes de chaque véhicule du groupe étudié se distribuent selon une loi de Pearson type III d'equation:

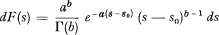
où Γ(b) est la fonction eulérienne de 21ème espèce:

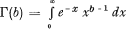
a, b, et S0 étant des paramètres dont la valeur est calculée en égalant les expressions des 3 premiers moments théoriques aux moments correspondants observés.

Cette formule conduit à des calculs assez longs.

M. Depoid a proposé une formule plus simple.