By using the spectral Galerkin method, we prove a result on the global existence in time of strong solutions for a system of equations of magnetohydrodynamic type. Several estimates for the solution and their approximations are given. These estimates can be used in the derivation of error bounds for the approximate solutions.

In a recent paper, Christie and Gopalsamy [2] used Melnikov's method to establish a sufficient condition for the existence of chaotic behaviour, in the sense of Smale, in a particular time-periodically perturbed planar autonomous system of ordinary differential equations. They then concluded with an application to the dynamics of a one-dimensional anharmonic oscillator. In this paper, the same system is considered and a condition for the existence of subharmonic orbits in the perturbed system is deduced, using the subharmonic Melnikov theory. Finally, an application is given to the dynamical behaviour of the one-dimensional anharmonic oscillator system.

The paper is concerned with formation of singularities in a density stratified fluid subject to a monochromatic point source of frequency σ. The frequency of the source is assumed to be such that the steady-oscillation equation is hyperbolic in the neighbourhood of the source and degenerates at a critical level. We obtain asymptotic formulae demonstrating how the solution diverges as t → ∞ on the characteristic surface emanating from the source. It is shown that, at points of the surface that belong to the critical level, the solution behaves as t⅔ exp {i(σt + π/2)} as t → ∞, whereas its large time behaviour at the other points of the surface is given by t½ exp {i(σt + π/2 ± π/4)}.

The resolution of many problems in probability depends on being able to provide sufficiently good upper or lower bounds to certain moments of distributions. A striking example from the literature of a result that can offer such bounds was given by Pó1ya over sixty years ago as the following theorem (see [7, Vol. II, p. 144] and [7, Vol. I, p. 94]).

In this paper we present an adaptive boundary-element method for a transmission prob-lem for the Laplacian in a two-dimensional Lipschitz domain. We are concerned with an equivalent system of boundary-integral equations of the first kind (on the transmission boundary) involving weakly-singular, singular and hypersingular integral operators. For the h-version boundary-element (Galerkin) discretization we derive an a posteriori error estimate which guarantees a given bound for the error in the energy norm (up to a multiplicative constant). Then, following Eriksson and Johnson this yields an adaptive algorithm steering the mesh refinement. Numerical examples confirm that our adaptive algorithms yield automatically good triangulations and are efficient.

We describe a C0-collocation-like method for solving two-dimensional elliptic Dirichlet problems on rectangular regions, using tensor products of continuous piecewise polynomials. Nodes of the Lobatto quadrature formula are taken as the points of collocation. We show that the method is stable and convergent with order hr(r ≥ 1) in the H1–norm and hr+1(r ≥ 2) in the L2–norm, if the collocation solution js a piecewise polynomial of degree not greater than r with respect to each variable. The method has an advantage over the Galerkin procedure for the same space in that no integrals need be evaluated or approximated.

This paper derives key equations for the determination of optimal control strategies in an important engineering application. A train travels from one station to the next along a track with continuously varying gradient. The journey must be completed within a given time and it is desirable to minimise fuel consumption. We assume that only certain discrete throttle settings are possible and that each setting determines a constant rate of fuel supply. This assumption is based on the control mechanism for a typical diesel-electric locomotive. For each setting the power developed by the locomotive is directly proportional to the rate of fuel supply. We assume a single level of braking acceleration. For each fixed finite sequence of control settings we show that fuel consumption is minimised only if the settings are changed when certain key equations are satisfied. The strategy determined by these equations is called a strategy of optimal type. We show that the equations can be derived using an intuitive limit procedure applied to corresponding equations obtained by Howlett [9, 10] in the case of a piecewise constant gradient. The equations will also be derived directly by extending the methods used by Howlett. We discuss a basic solution procedure for the key equations and apply the procedure to find a strategy of optimal type in appropriate specific examples.

The generalised elliptic-type integral Rμ(k, α, γ)

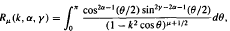
where 0 ≤ k < 1, Re(γ) > Re(α) > 0, Re(μ) ≥ −0.5, is represented in terms of the Gauss hypergeometric function by Kalla, Conde and Hubbell [8]. In 1987, Kalla, Lubner and Hubbell derived a simple-structured single-term approximation for this function in the neighbourhood of k2 = 1 in some range of the parameters α, γ and μ. Another formula which complements the parameter range was recently derived by the author. In this paper a novel technique is used in deriving multiple-term efficient approximations (in the neighbourhood of k2 = 1) which may be considered as a generalisation to the concept of the single-term approximations mentioned above. Two non-overlapping expressions which almost cover the entire range of parameters (α, γ, μ) are derived. Closed-form solutions are obtained for single- and double-term approximations (in the neighbourhood of k2 = 1). Results show that the proposed technique is superior to existing approximations for the same number of terms. Our formulation has potential application for a wide class of special functions.