Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T09:10:40.886Z Has data issue: false hasContentIssue false
  • English
  • Français

Equations for periodic solutions of a logistic difference equation

Published online by Cambridge University Press:  17 February 2009

A. Brown
A. Brown
Affiliation:
Department of Applied Mathematics, Faculty of Science, Australian National University, Canberra, A.C.T. 2600
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper is concerned with periodic solutions of the difference equation un + 1 = 2aun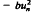, where a and b are constants, with 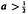and b > 0. A new method is developed for dealing with this problem and, for period lengths up to 6, polynomial equations are given which allow the periodic solutions to be determined in a precise and practical manner. These equations apply whether the periodic solutions are stable or unstable and the elements of the cycle can be determined with an accuracy which is not affected by instability of the cycle.

A simple transformation puts the equation into the form 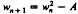, where A = a2 − a, and the detailed discussion is based on this simpler form. The discussion includes details such as the number of cyclic solutions for a given value of A, the pattern of the cycles and their stability. For practical purposes, it is enough to consider a restricted range of values of A, namely 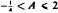, although the equations obtained are valid for A > 2.

Type
Research Article
Information
The ANZIAM Journal , Volume 23 , Issue 1 , July 1981 , pp. 78 - 94
Copyright
Copyright © Australian Mathematical Society 1981

References

[1]Chaundy, T. W. and Phillips, Eric, “The convergence of sequences defined by quadratic recurrence formulae” Quart. J. Math. (Oxford) 7 (1936), 74–80.Google Scholar
[2]Elton, C. S., Mice, voles and lemmings (O.U.P., 1942).Google Scholar
[3]Hoppensteadt, F. C. and Hyman, J. M., “Periodic solutions of a logistic difference equation”. SIAM J. Appl. Math. 32 (1977), 73–81.CrossRefGoogle Scholar
[4]Hurewicz, W., Lectures on ordinary differential equations (M.I.T. and Wiley, 1958).CrossRefGoogle Scholar
[5]Levin, S. A. and May, R. M., “A note on difference-delay equations”, Theoretical Population Biology 9 (1976), 178–187.CrossRefGoogle ScholarPubMed
[6]Li, T. Y. and Yorke, J. A., “Penod three implies chaos”, Amer. Math. Monthly 82 (1975), 985–992.CrossRefGoogle Scholar
[7]Lorenz, E. N., “The problem of deducing the climate from the governing equations”, Tellus 16 (1964), 1–11.CrossRefGoogle Scholar
[8]May, R. M., “Simple mathematical models with very complicated dynamics”, Nature 261 (1976), 459–467.CrossRefGoogle ScholarPubMed
[9]May, R. M. and Oster, G. F., “Bifurcation and dynamic complexity in simple ecological models”, The American Naturalist 110 (1976), 573–599.CrossRefGoogle Scholar
[10]Uspensky, J. V., Theory of equations (McGraw-Hill, 1948), Chapter 11.Google Scholar