In this paper we consider the asymptotics of extinction for the nonlinear diffusion reaction equation

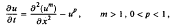
with non-negative initial data possessing finite support. For t > 0, both solution and support vanish as t → T and x → x0. With T as the extinction time we construct the asymptotic solution as τ = T – t → 0 near the extinction point x0 using matched expansions. Taking x0= 0, we first form an outer expansion valid when η =xt–(m–p)/2 (1–p) = 0(1). This is nonuniformly valid for large |η| and has to be replaced by an intermediate expansion valid for |x| = O(τ−1/l0) where l0 is an even integer greater than unity. If p + m ≥ 2 this expansion is uniformly valid while for p + m < 2, there are regions near the edge of the support where diffusion becomes important. The zero order solution in these inner regions is discussed numerically.