Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T10:43:31.876Z Has data issue: false hasContentIssue false
  • English
  • Français

The algebraic structure of relativistic wave equations

Published online by Cambridge University Press:  17 February 2009

A. Cant  and
C. A. Hurst
C. A. Hurst
Affiliation:
Department of Mathematical Physics, University of Adelaide, Adelaide, South Australia, 5001
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The algebraic structure of relativistic wave equations of the form

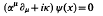
is considered. This leads to the problem of finding all Lie algebras L which contain the Lorentz Lie algebra so(3, 1) and also contain a “four-vector” αμ a such an L gives rise to a family of wave equations. The simplest possibility is the Bhabha equations where L≅so(5). Some authors have claimed that this is the only one, but it is shown that there are many other possibilities still in accord with physical requirements. Known facts about representations, along with Dynkin's theory of the embeddings of Lie algebras, are used to obtain a partial classification of wave equations. The discrete transformations C, P, T are also discussed, along with reality properties. Finally, a simple example of a family of wave equations based on L = sp(12) is considered in detail. The so(3, 1) content and mass spectra are given for the low order members of the family, and the problem of causality is briefly discussed.

Type
Research Article
Information
The ANZIAM Journal , Volume 20 , Issue 4 , December 1978 , pp. 446 - 486
Copyright
Copyright © Australian Mathematical Society 1978

References

[1]Dirac, P. A. M., Proc. Roy. Soc. (London) A 115 (1936), 447–459.Google Scholar
[2]Fierz, M., Helv. Phys. Acta 12 (1939), 3–37.CrossRefGoogle Scholar
Pauli, W. and Fierz, M., Helv. Phys. Acta 12 (1939), 297–300.Google Scholar
Fierz, M. and Pauli, W., Proc. Roy. Soc. A 173 (1939), 211–232.Google Scholar
[3]Bhabha, H. J., Rev. Mod. Phys. 17 (1945), 200–216.CrossRefGoogle Scholar
[4]Harish-Chandra, , Phys. Rev. 71 (1947), 793–805.CrossRefGoogle Scholar
[5]Le Couteur, K. J., Proc. Roy. Soc. (London) A 202 (1950), 284–300, 394–407.Google Scholar
[6]Gel'fand, I. M. and Yaglom, A. M., Z. Èksper. Teoret. Fiz. 18 (1948), 703–733, 1096–1104, 1105–1111.Google Scholar
[7]Corson, E. M., An introduction to tensors, spinors and relativistic wave equations(Blackie, 1953).Google Scholar
[8]Gel'fand, I. M., Minlos, R. A. and Ya, Z.. Shapiro, Representations of the rotation and Lorentz groups and their applications (Pergamon Press, 1963).Google Scholar
[9]Bauer, F. L., Sitzb. d. Bay. Akad. d. Wiss. 13 (1952), 111–179.Google Scholar
[10]Lorente, M., Huddleston, P. L. and Roman, P., J. Math. Phys. 14 (1973), 1495–1497.CrossRefGoogle Scholar
[11]Biritz, H., Nuov. Cim. B 25 (1975), 449–478.CrossRefGoogle Scholar
[12]Dynkin, E. B., Amer. Math. Soc. Transl. (Ser. 2) 6 (1957), 111–244.CrossRefGoogle Scholar
[13]Kursunoglu, B., Phys. Rev. 167 (1968), 1452–1461.CrossRefGoogle Scholar
[14]Navon, A. and Patera, J., J. Math. Phys. 8 (1967), 489–493.CrossRefGoogle Scholar
[15]Humphreys, J. E., Introduction to Lie algebras and representation theory (Springer-Verlag, 1972).CrossRefGoogle Scholar
[16]King, R. C., J. Phys. A 8 (1975), 429–449.CrossRefGoogle Scholar
[17]Samelson, H., Notes on Lie algebras (Van Nostrand Reinhold, 1969).Google Scholar
[18]Wightrnan, A. S., “Stability of representations of the Poincaré group”, in Symmetry principles at high energy, Fifth Coral Gables Conference (ed. Perlmutter, A., Hurst, C. A. and Kursunoglu, B.) (W. A. Benjamin, 1968).Google Scholar
[19]Wybourne, B. G., Symmetry principles and atomic spectroscopy, (Wiley-Interscience, 1970).CrossRefGoogle Scholar
[20]Yutsis, A. P., Levinson, I. B. and Vanagas, V. V., Theory of angular momentum, (Israel Program for Scientific Translations, 1962).Google Scholar
[21]Konuma, M., Shima, K. and Wada, M., Progr. Theoret. Phys. (Japan) Suppl. 28 (1963), 1–127.CrossRefGoogle Scholar
[22]Jacobson, N., Lie algebras (Interscience, 1962).Google Scholar
[23]Krajcik, R. A. and Nieto, M. M., Phys. Rev. D 13 (1976), 924–941.CrossRefGoogle Scholar
[24]Velo, G. and Zwanziger, D., “Acausality and higher spin equations”, in Tracts in mathematics and natural sciences Vol. 4 (Gordon and Breach, 1971).Google Scholar
[25]Stoyanov, D. Tz. and Todorov, I. T., J. Math. Phys. 9 (1968), 2146–2167.CrossRefGoogle Scholar
[26]Demazure, M., Bull. Sci. Math. 2e série 98 (1974), 163–172.Google Scholar
[27]Tarski, J., J. Math. Phys. 4 (1963), 569–574.CrossRefGoogle Scholar
[28]Gruber, B. and Zaccaria, F., Suppl. at Nuovo Cimento 5 (1967), 914–936.Google Scholar
[29]Bracken, A. J., J. Phys. A 8 (1975), 800–807.CrossRefGoogle Scholar
[30]Krajcik, R. A. and Nieto, M. M., Phys. Rev. D 14 (1976), 418–436.CrossRefGoogle Scholar
[31]Santhanam, T. S., J. Math. Phys. 10 (1969), 1704–1710.CrossRefGoogle Scholar