Introduction
Among the earliest scientific investigations into the nature and phenomenology of icebergs is the analysis of their orientational stability and their tendency to capsize and roll. Aside from being a mathematically interesting problem (e.g. Reference Nye and PotterNye and Potter, 1980), interest in orientational stability stems from the practical challenges facing the offshore petroleum industry (e.g. Reference AllaireAllaire, 1972; Reference Lewis and BennettLewis and Bennett, 1984) and from past consideration of icebergs as a freshwater source (e.g. Reference BassBass, 1980; Reference WeeksWeeks, 1980).
Another phenomenon of icebergs related to their orientational stability is the fact that iceberg capsize can generate large surface waves, or tsunamis, which can be hazardous to humans in the immediate vicinity (e.g. as illustrated by a video of a tsunami causing material damage in a Greenlandic fishing harbour in 1995; search for ‘Greenland tsunami’ on www.youtube.com).
Iceberg tsunamigenesis accompanying calving events at the termini of Greenland outlet glaciers has been observed using tide-gauge and seismometer instruments (e.g. Reference Amundson, Truffer, Lüthi, West and MotykaAmundson and others, 2008, Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and Motyka2010). Many of these iceberg tsunamis are also observed to accompany glacial earthquakes detected teleseismically (at seismometer stations far from Greenland; Reference NettlesNettles and others, 2008). These tsunamis sometimes trigger secondary iceberg calving at the termini of Greenland outlet glaciers; see the time-lapse videos of calving events presented as auxiliary materials in Reference Amundson, Truffer, Lüthi, West and MotykaAmundson and others (2008, Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and Motyka2010). Iceberg tsunamigenesis is also routinely observed in the Antarctic (Reference MacAyeal, Okal, Aster and BassisMacAyeal and others, 2009), and has been proposed as a possible energy source for catastrophic ice-shelf break-up such as that witnessed recently for the Larsen B and Wilkins ice shelves (Reference MacAyeal, Scambos, Hulbe and FahnestockMacAyeal and others, 2003; Reference ScambosScambos and others, 2009; Guttenburg and others, in press).
The purpose of the present paper is to evaluate the tsunami source mechanism associated with iceberg capsize using simple energy analysis. Although there are other iceberg tsunami source mechanisms, such as iceberg infall from elevated calving faces of tidewater glaciers, our attention is focused on the iceberg-capsize source because we believe this is the mechanism that: (a) poses the least-recognized practical hazard to humans of all the calving-related tsunamigenesis mechanisms and (b) is most important to the dynamics of ice-mélange choked fjords in Greenland and collapsing ice shelves in Antarctica. In contrast, calving from tidewater faces occurs in a relatively fixed location where the tsunami risk is generally well appreciated by people experienced in the nature of the local terrain.
Iceberg-Capsize Source Energetics
A comprehensive treatment of iceberg tsunamigenesis is challenging to both create and interpret, especially if the hydrodynamics of wave generation is to be related to the specific geometry of iceberg and basin. To overcome these challenges, and to determine a simple rule-of-thumb treatment useful for assessing hazards in practical circumstances where information about iceberg geometry is limited, we adopt a simple ‘before and after’ capsize potential energy assessment to yield an upper bound on the energy available to a surface-gravity wave. The exact details of a specific iceberg-capsize event (e.g. The size and shape of the iceberg, the rate and direction in which it rolls and the local bathymetry and hydrography) will all contribute to determining the characteristics of the outgoing wave and the degree to which energy released by capsize is channelled into other forms of motion. The role of these exact details in iceberg tsunamigenesis is relegated to future study.
As depicted in Figure 1, we consider an idealized, two-dimensional iceberg of homogeneous density ρ i < ρ w described by two parameters: H, the initial iceberg thickness, and ϵ, the ratio of initial iceberg width to thickness. The water in which the iceberg floats is assumed to be homogeneous and to have density ρ w. We assume that the iceberg has previously calved from a floating ice tongue or ice shelf, is floating in equilibrium, is at rest and is thicker than it is wide, that is ϵ ≤ 1.

Fig. 1. To compute the energy, ΔE, liberated by iceberg capsize, the difference between the work required to lift the iceberg in each of its two orientational states to a fixed reference level above the water is found. To compute this work, both the force of gravity and the force of pressure acting on the basal face of the iceberg are accounted for. The potential energy of the initial uncapsized iceberg is greater than that of the capsized iceberg. This difference, ΔE, is the energy that is released into dissipative processes, including the radiation of tsunami wave energy.
Tsunami Energetics
We next consider the problem of estimating the fraction of energy released by iceberg capsize that is transferred to a tsunami, that is the ratio E T /ΔE, where E T is the energy of the tsunami. The simplest estimate, that all the energy of capsize is transferred to the tsunami, is inappropriate because there are at least five other modes of iceberg/ocean behaviour into which energy can be partitioned following the capsize. As well as the E T of an impulsive, leading surface wave identified as the tsunami, energy can be partitioned into:
-
1. a long train of following surface waves of varying wavelength (see fig. 2.4 of Reference FritzFritz, 2002) and kinetic energy of the iceberg in translation equal to 1/2ρ i ϵH 2 U 2 where U is the horizontal velocity of the iceberg;
-
2. bobbing and rocking motions of the iceberg/water system described by Reference SchwerdtfegerSchwerdtfeger (1980);
-
3. work done against dissipational forces associated with viscosity of water;
-
4. work done against the forces required to move surface ice melange (if present); and finally
-
5. work done by mixing against buoyancy, if the water column is stratified.
Depending on the value of ϵ and the ratio of ice and water densities ρ i /ρ w, the tendency to capsize can be either unconditional, that is capsize will result from any infinitesimal perturbation to the initial upright orientation, or conditioned on some process overcoming an initial resistance to capsize, as described by Reference BassBass (1980) and Reference Nye and PotterNye and Potter (1980). In the analysis, the distinction between conditional and unconditional stability is not pertinent to the total energy released by capsize; however, we do not account for the energy associated with whatever process is needed to overcome initial energy barriers to capsize. (As discussed by Reference MacAyeal, Okal, Aster and BassisMacAyeal and others (2009), the processes that overcome initial resistance to capsize could include tsunamis generated by neighbouring icebergs. This could be a factor in runaway ice-shelf disintegrations of the Antarctic.)
The total energy released by iceberg capsize ΔE is the difference between the initial and final gravitational potential energies of the iceberg/water system at rest (after all motions have died away). To evaluate ΔE in terms of the parameters of the idealized iceberg, we perform a theoretical computation of work done, W, against gravity and pressure forces, F g and F p respectively, to lift the iceberg from the water to an arbitrary fixed reference level above the water surface. It is essential that this theoretical computation uses the expression for hydrostatic equilibrium in computing work done by pressure forces on the basal face of the iceberg (as depicted in Fig. 1). If the task of lifting the iceberg from the water was carried out in real life, the process would have to be done slowly enough to avoid invoking non-hydrostatic pressures that represent the inertia of the water. By restricting the work done by the water on the iceberg to that associated with hydrostatic pressure only, reversible changes in the static potential energy of the water distribution are accounted for.
We take the fixed reference level of the theoretical work computation outlined above to be the elevation of the centre of mass of the initial iceberg after it has been raised vertically to the point of having its lower face just touching the ocean surface (Fig. 1). The work required to lift the pre-capsized iceberg is the sum of: (a) the work done against the force of gravity, F g = ρ igϵH 2(−nz), and (b) the work done by the pressure force acting on the basal surface of the iceberg, F p = (ρ wgz)(ϵH)(nz), where z = 0 is the undisturbed surface of the water with z positive upwards and nz is a unit vector in the positive z direction. The increment of vertical displacement is dznz , which is positive. This sum can be expressed as follows (noting that nz · nz = 1):
The two integrals are evaluated to give
or
Recall that a negative work, such as that represented by the first term on the right-hand side of Equation (2), implies that potential energy is increased. The integral expression for W f , the work associated with lifting the capsized iceberg to the same reference position where its centre of mass is also at z = H/2, is readily evaluated by (a) substituting ϵH for H in the lower limits of integration of the two integrals and (b) replacing the area of the basal face ϵH with H on the right-hand side of Equation (1):
This expression is evaluated to give
or
The total energy released by the iceberg capsize, ΔE = W i −W f , is found to be:
Note that, in the above expression, ΔE ≥ 0 for ϵ ≤ 1. This means that more energy is required to lift the precapsized iceberg from the water than to lift the capsized iceberg. The missing energy is available to be radiated away from the iceberg by surface waves in the water. The factor of ϵ(1 − ϵ) in Equation (7) ensures that ΔE → 0 as ϵ → 0, 1. When ϵ = 0, the iceberg has infinitesimal mass and thus cannot generate potential energy changes by any orientational change. When ϵ = 1, the potential energy of the iceberg is equal in both orientations, so no net change of energy is possible from capsize. Note that energy is a function of H 3, which implies that icebergs from thick ice tongues (such as those calved from outlet glaciers terminating in Greenland fjords) can have a greater ability to generate tsunamis than icebergs calved from the typically thinner ice shelves of the Antarctic.
For an insight into iceberg-capsize energetics, we plot ΔE for a range of ϵ values and for a fixed thickness H = 300m – typical of ice shelves in the Antarctic – in Figure 2. As anticipated, the energy available for waves radiated from a capsizing iceberg of rectangular geometry, with ρ i = 910 kg m − 3, ρ w = 1030 kg m − 3 and ϵ = 1/2, is 3.51 × 109 Jm − 1 for each metre of iceberg width in the unresolved dimension. In Greenlandic settings where icebergs can commonly be 1000 m thick and >1000m wide in the unresolved horizontal dimension (Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and MotykaAmundson and others, 2010), capsize energy can amount to the explosive energy of tens of kilotons of TNT (1 ton = 4.184 × 109 J).

Fig. 2. Iceberg-capsize energy ΔE expressed in joules per unit metre of iceberg length in the unresolved dimension for an iceberg of thickness H = 300 m as a function of ϵ.
That ΔE can be distributed among six post-capsize modes of energy suggests that laboratory experiments or numerical methods are needed to assess this energy transfer.
As a prelude to laboratory and numerical analysis (both beyond the scope of the present study), we use scaling relationships to express E T /ΔE in terms of fundamental parameters of the problem. This approach has merit for a general descriptive assessment of tsunami hazard and has been developed extensively from laboratory work and observations of the tsunami energetics associated with earthquake and landslide sources (e.g. Reference FritzFritz, 2002; Reference OkalOkal, 2003; Reference Okal and SynolakisOkal and Synolakis, 2003; Reference Dutykh and DiasDutykh and Dias, 2009).
Following the similarity analysis of Reference FritzFritz (2002), we use the Buckingham Π theorem (Reference BuckinghamBuckingham, 1914) to identify the dimensionless parameters of the problem that will govern E T /ΔE. The Buckingham Π theorem states that if a physical process can be expressed by an equation relating n physical variables that involve k fundamental physical quantities, the process can also be described by an appropriate dimensionless equation involving a set of p = n − k dimensionless parameters composed of the physical variables.
For iceberg-capsize tsunamigenesis, we propose that there are six physical variables assumed to be at play in the source mechanism: ice density ρ i, water density ρ w, gravitational acceleration g, ice thickness H, iceberg aspect ratio ϵ and the depth of water D. The three fundamental physical quantities involved in the iceberg-capsize problem are mass, length and time. The Buckingham Π theorem states that, at iceberg capsize, tsunamigenesis will be governed by three non-dimensional parameters. The Buckingham Π theorem does not, however, provide a means to specify these non-dimensional parameters. For this, we rely on physical intuition and the results of previous experiments and observations (e.g. Reference FritzFritz, 2002).
The three non-dimensional parameters we shall use here are
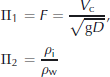
and
where V c = ϵH/T c (to be derived below) is a translational velocity that represents the rate of capsize (i.e. The rate at which a side of the iceberg moves either vertically or horizontally during its rotational motion). T c is the timescale of capsize that depends on moments of inertia and buoyancy torques that are themselves dependent on fundamental parameters of the system.
The first and most important parameter Π1 is the Froude number F. The second two parameters are involved in our analysis because buoyancy and the moment of inertia, which is related to H and ϵ, affect the speed and timescale of capsize, V
c and T
c, respectively. The factor ![]() appearing in Π1 = F is the characteristic phase velocity of surface waves in the water surrounding the iceberg. We do not distinguish between shallow-water phase speed and deep-water phase speed because we assume that iceberg capsize happens primarily in shallow water, where the dimensions of the iceberg are comparable to the depth of water.
appearing in Π1 = F is the characteristic phase velocity of surface waves in the water surrounding the iceberg. We do not distinguish between shallow-water phase speed and deep-water phase speed because we assume that iceberg capsize happens primarily in shallow water, where the dimensions of the iceberg are comparable to the depth of water.
Because capsize is a process that initiates as a rocking motion, we evaluate T c in the expression for V c and hence F, using the quarter-period of rocking oscillations given by Reference SchwerdtfegerSchwerdtfeger (1980):
This gives the following expression for Π1 = F:
Evaluating the above expression for typical values of ρ w /ρ i gives F ≤ 0.5 with F → 0 as ϵ → 0. For the most energetic capsize associated with ϵ = 1/2, F ∼ 0.2. It should be noted that F is generally much smaller, that is F < 1, for iceberg-capsize tsunamigenesis than for some landslide forms of tsunamigenesis, such as those studied by Reference FritzFritz (2002). This difference will guide us to propose a scaling relationship for E T /ΔE that is appropriate for small F, which we anticipate as being of a form that requires E T /ΔE → 0 as F → 0.
The Buckingham Π theorem states that E T /ΔE can be expressed as some function G of the three non-dimensional parameters, that is
The problem is that the Buckingham Π theorem does not inform us how to specify this function. Hydrodynamic analysis using laboratory experiments, observations and numerical models is required to specify G. An example of how this is done using laboratory experiments is provided by Reference FritzFritz (2002); however, we note that the physics of his experiments involved additional Π-parameters and involved Froude numbers larger than the values (< 1) associated with iceberg capsize. In the present study, we avoid performing otherwise requisite laboratory or numerical experiments. We proceed by proposing a simple working expression for G that satisfies E T /ΔE ≤ 1 with E T /ΔE → 0 as each of the Π parameters → 0.
This working expression is
This choice has the advantage of satisfying the requirement that E T /ΔE < 1. F is represented in this expression with an exponent of 2, reflecting the fact that energy is typically related to the square of the velocity. F is composed of a ratio of velocities. With this working guess for G and the typical density ratio, the energy ratio varies between 0 and 0.16 as ϵ = 0 → 1, with E T /ΔE ∼ 0.02 for the most energetic capsize associated with ϵ = 1/2. Note that the above choice of G is not unique, and is based entirely on a guess that represents a first step towards simplifying the physical problem. The guess we employ here was chosen to be a function that would give a result between 0 and 1 and that would scale as F 2 for F ≪ 1.
Submarine landslide analogy
Another approach to estimating the energy of a tsunami generated by iceberg capsize is to assume that the process is similar to the tsunami source mechanism associated with submarine landslides. This similarity is seen from the fact that both iceberg capsize and submarine landslides are mass movements that occur at either the top or bottom interface of the water layer. Indeed, the iceberg-capsize process can be seen as equivalent to an initial mass at the top surface of the water that has a thickness (ρ i /ρ w)H and width ϵH that slides in a manner to have a final thickness of ϵ(ρ i /ρ w)H and width H. The problem of submarine landslides has been considered by Reference OkalOkal (2003), who shows (see his equation (38)) that
where S is the area of landslide material, Δh is the thickness of landslide material, Δz is the vertical distance the landslide moves, ρ s is the density of landslide material and d is the depth of the water (source depth of the tsunami). Taking the above scaling relationship at face value and substituting parameters describing iceberg capsize for the submarine landslide parameters,
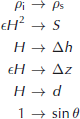
and we obtain
Equation (13) implies that about 7% of the energy released by the iceberg capsize goes into an initial tsunami pulse that radiates into the far field. This result is within an order of magnitude of the result expressed using the Π theorem and provides an estimate of how the energy ratio depends on the Froude number.
Tsunami Amplitude
The final step in assessing iceberg-tsunami hazard is to use the above ratios of energy conversion to estimate tsunami height. What makes this step difficult is the fact that the source mechanism can possess directivity, that is a circumstance where energy is radiated preferentially in a narrow field, and dispersion, that is a circumstance where energy is radiated into a spectrum of wavelengths that disperse over time and thus reduce local wave amplitude. Additional aspects associated with geometric spreading and with coastal geometry and bathymetry are also extremely important in determining run-up potential and therefore hazards to humans and human infrastructure. In the present study, we estimate tsunami height in open water (meaning not immediately adjacent to either the iceberg or a shoreline) using a simple scaling relationship involving tsunami energy.
We assume that the simple energy scaling relationship between tsunami height and energy is
where h is the height of a solitary ‘hump’ of water travelling away from the iceberg in both directions and L is the length scale of this hump. To estimate L, we compute a length scale from the time taken to capsize, T
c, and the phase velocity of surface waves, ![]() Assuming D ∼ H,
Assuming D ∼ H,
Using the expressions for ΔE and the ratio G = rE T /ΔE, the following rule-of-thumb estimate of h in terms of H is derived as
where the division of G by 2 accounts for the fact that the tsunami radiates in two directions, with half of the energy assumed to be partitioned into each direction. Assuming that the ratio G is approximately 0.05 (a value between the two crude estimates given in the previous section), the above relation reduces to
for ϵ = 1/2. For the capsize of a 300m thick iceberg with ϵ = 1/2, the resulting tsunami amplitude is h ∼ 3m. The result for an initial thickness of 1000m is h ∼ 10 m.
Discussion and Conclusions
Two basic questions remain to be answered. First, is the above estimate of iceberg tsunamigenic height (or amplitude) reasonable? Second, how can humans best use the information derived here to reduce risk associated with iceberg tsunamis?
The first question is difficult to answer because there are few observations of the amplitude of tsunamis in the near-field close to the source prior to tsunami height changes associated with geometric spreading, dispersion and shoreline run-up. The relatively few forms of observation that exist use time-lapse photography, seismometers and underwater pressure sensors to investigate tsunamis generated by iceberg calving and capsize in Greenlandic fjords (e.g. Reference JoughinJoughin and others, 2008; Reference NettlesNettles and others, 2008; Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and MotykaAmundson and others, 2010). These observations suggest that, near the point of calving, there are indeed large-amplitude surface-water movements. A time-lapse video of the capsize of an iceberg approximately 1000m thick on 5 June 2007 from Jakobshavn Isbræ (see movie S1 published as auxiliary material with Reference Amundson, Truffer, Lüthi, West and MotykaAmundson and others, 2008) is particularly informative about the effects of iceberg capsize in Greenlandic fjords.
The rule of thumb given by Equation (17) suggests that a tsunami height of 10m could result from the capsize of icebergs from Jakobshavn Isbræ with typical thicknesses up to 1000 m. The video shows that the iceberg capsize creates a splash of water that inundates the surface of the glacier behind the ice front, which stands approximately 100m tall. This splash, however, exhibits extremely nonlinear hydrodynamics (i.e. is in the form of a plume of water droplets on various ballistic trajectories) and is thus not likely part of the tsunami. The tsunami generated by this iceberg capsize is seen propagating away from the source through the densely covered ice-melange surface with a height that is difficult to distinguish given the lack of scale in the photography; a height of <10m seems consistent with a casual interpretation of what is visible in the video, however.
A pressure sensor located in an open pool ∼5km from the Jakobshavn calving front recorded tsunami amplitudes of ∼2m on a routine basis (Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and MotykaAmundson and others, 2010). These observations, while not definitive, suggest that the rule of thumb derived on the basis of scaling arguments (h ∼ 1 × 10 − 2 H) provides a reasonable upper bound on tsunami height that can be used for risk assessment.
To answer the second question, it is important to inform people that (1) icebergs can produce tsunamis that are sufficiently energetic to pose a threat to life and property and (2) the quantification of risk in terms of possible tsunami height is not a trivial scientific problem. It is one which requires further research and, at present, must rely on simple rules of thumb that are at best guesses at upper bounds of tsunami danger.
Acknowledgements
This work is supported by the US National Science Foundation under grants ANT-0944193, OPP-0838811 and CMG-0934534. D.S.A. was supported by the T.C. Chamberlin Fellowship of the University of Chicago and the Canadian Institute for Advanced Research. We thank E. Okal, J. Bassis, M. Cathles, N. Guttenberg, J. Burton, W. Zhang and especially J. Amundson, whose time-lapse videos of Greenlandic iceberg capsize inspired this work. The reviews of P. Bartelt, M. Naaim, an anonymous referee and the internal review provided by J. Amundson led to improvements in the paper.




