2. Partial dependence functions

The PD function w.r.t. a, potentially exogenously given, (mean) function $\mu (x)$ , $x' = (x_1, \ldots, x_d)' \in \mathbb{X}$ , and the covariates $x_{\mathcal{A}}$ , $\mathcal{A} \subset \{1, \ldots, d\}$ , is given by:

(5) \begin{align} {\mathrm{PD}}(x_{\mathcal{A}}) \;:\!=\; \int \mu (x_{\mathcal{A}}, x_{\mathcal{A}^{{\mathrm{C}}}}){{\mathrm{d}}} \mathbb{P}(x_{\mathcal{A}^{\mathrm{C}}}), \end{align}

where $\mathcal{A}^{\mathrm{C}} = \{1, \ldots, d\} \setminus \mathcal A$ , see e.g. Friedman and Popescu (Reference Friedman and Popescu2008). Note that Equation (5) can be rephrased according to

(6) \begin{align} {\mathrm{PD}}(x_{\mathcal{A}}) ={\mathbb{E}}[\mu (x_{\mathcal{A}}, X_{\mathcal{A}^{\mathrm{C}}})], \end{align}

which illustrates that ${\mathrm{PD}}(x_{\mathcal{A}})$ quantifies the expected effect of $X_{\mathcal{A}} = x_{\mathcal{A}}$ , when breaking all potential dependence between $X_{\mathcal{A}}$ and $X_{\mathcal{A}^{\mathrm{C}}}$ , see Friedman and Popescu (Reference Friedman and Popescu2008). In particular, note that if $\mu (x) \;:\!=\;{\mathbb{E}}[Y \mid X = x]$ , the PD function w.r.t. $\mathcal{A}$ is related to the expected effect of $\mathcal{A}$ on $Y$ , when adjusting for potential association between $X_{\mathcal{A}}$ and $X_{\mathcal{A}^{\mathrm{C}}}$ , see Zhao and Hastie (Reference Zhao and Hastie2021). Henceforth, all references to $\mu$ will, unless stated explicitly, treat $\mu$ as a conditional expected value of $Y$ .

2.1 Implications of partial dependence functions

From Section 2, we know that the PD function describes the expected effect that a covariate, or a subset of covariates, has on $Y$ , when adjusting for the possible dependence between covariates, recall Remark1(a). Further, since the PD functions measure the influence of (subsets of) covariates deduced from $\mu (x)$ , i.e. not on the link-function transformed scale, the use of PD functions is not expected to identify marginal or interaction effects in the standard sense. In order to illustrate this, consider the following log-linear additive model:

(8) \begin{align} \mu (x) \;:\!=\; \exp \left \{\beta _0 + \sum _{k = 1}^d f_k(x_k) + \sum _{k = 1}^d\sum _{j \lt k} f_{j, k}(x_j, x_k)\right \}, \end{align}

where the $f$ s are, e.g., basis functions. Hence, if we let $\mathcal A = \{j\}$ , and introduce $x_{\setminus j} \;:\!=\; x_{\mathcal{A}^{\mathrm{C}}}$ , it follows that the PD based on Equation (8) w.r.t. $x_j$ reduces to

(9) \begin{align} {\mathrm{PD}}(x_j) &={\exp \{f_j(x_j)\}\exp \{\beta _0\}\int \exp \left \{\sum _{k \neq j} f_k(x_k) + \sum _{k = 1}^d\sum _{j \lt k} f_{j, k}(x_j, x_k)\right \}{{\mathrm{d}}} \mathbb{P}(x_{\setminus j})}\nonumber \\[5pt] &= \exp \{f_j(x_j)\} \nu _{\setminus j}(x_j). \end{align}

That is, the PD function provides a marginalized effect of $x_j$ on $Y$ deduced from $\mu (x)$ , but it is in general not the same as $\exp \{f_j(x_j)\}$ . This, however, is expected, since based on Equation (8), it is clear that the component $f_j(x_j)$ does not have the meaning of a unique marginal effect of $x_j$ on $Y$ , due to the presence of the $f_{j,k}$ s. Thus, changes in the PD function w.r.t. $x_j$ are related to changes in the $j$ th dimension of $\mu (x)$ , when adjusting for possible dependence between $X_j$ and $X_{\setminus \{j\}}$ , see Remark1(a). Further, note that as discussed in the introduction, for our purposes the PD function is only used to construct covariate partitions. Thus, whether the absolute level of a marginal effect is correct or not, is of considerably less importance. We will come back to this discussion when describing how to construct covariate partitions in Section 2.2, see also Remark2(a) below.

Further, note that if $f_{j, k}(\cdot ) = 0$ for all $j, k$ , it follows that

(10) \begin{align} {\mathrm{PD}}(x_j) \propto \exp \{f_j(x_j)\}. \end{align}

In this situation, $\exp \{f_j(x_j)\}$ truly corresponds to the expected direct effect of $x_j$ on $Y$ , and this is, up to scaling, captured by the PD function. However, as pointed out above, this identifiability is not vital for our purposes.

Similarly, if we instead consider bivariate PD functions and consider $\mathcal{A} = \{j, k\}$ , with $x_{\setminus \{j, k\}} \;:\!=\; x_{\mathcal{A}^{\mathrm{C}}}$ , analogous calculations to those for the univariate PD functions yield

(11) \begin{align} {\mathrm{PD}}(x_j, x_k) &= \exp \{f_j(x_j) + f_k(x_k) + f_{j, k}(x_j, x_k)\}\nu _{\setminus \{j, k\}}(x_j, x_k). \end{align}

This illustrates how the bivariate PD function describes the expected joint effect of $x_j$ and $x_k$ on $Y$ deduced from $\mu (x)$ , which, as expected, is different from identifying $\exp \{f_{j, k}(x_j, x_k)\}$ .

Similar relations hold for other link functions than the log-link, but in this short note, focus will be on the log-link function.

Before ending this discussion, one can note that for the log-link it is possible to introduce an alternative identification. In order to see this, consider the situation where $\mu (x)$ is given by Equation (8) with only two covariates, $x_1, x_2$ , and (for ease of notation) no intercept. Based on Equation (9), introduce $g_j(x_i), j = 1, 2$ , such that

\begin{equation*} \exp \{g_j(x_j)\} \;:\!=\; \exp \{f_j(x_j)\} \nu _{\setminus j}(x_j), \end{equation*}

and introduce $g_{1, 2}(x_1, x_2)$ such that

\begin{equation*} \exp \{g_1(x_1) + g_2(x_2) + g_{1, 2}(x_1, x_2)\} \;:\!=\; \mu (x), \end{equation*}

i.e.

\begin{equation*} \exp \{g_{1, 2}(x_1, x_2)\} \;:\!=\; \frac {\exp \{f_{1, 2}(x_1, x_2)\}}{\nu _{\setminus 1}(x_1)\nu _{\setminus 2}(x_2)}. \end{equation*}

Thus, by construction, it then holds that

\begin{equation*} {\mathrm {PD}}(x_j) = \exp \{g_j(x_j)\}, \, j = 1, 2, \end{equation*}

together with that

\begin{equation*} \frac {{\mathrm {PD}}(x_1, x_2)}{{\mathrm {PD}}(x_1){\mathrm {PD}}(x_2)} = \exp \{g_{1, 2}(x_1, x_2)\}, \end{equation*}

which provides us with identifiability w.r.t. alternative factor effects given by $g_1(x_1), g_2(x_2)$ , and $g_{1, 2}(x_1, x_2)$ .

From the above discussion of $\mathrm{PD}$ functions, it is clear that these may serve as a way to identify the sensitivity of a covariate, or set of covariates, with respect to $\mu (x)$ . This is precisely how the $\mathrm{PD}$ functions will be used for covariate engineering purposes in Sections 2.2 and 3.

2.2 Covariate engineering, PD functions, and marginal auto-calibration

As discussed when introducing the expectation representation of the PD function in Equation (6), see also Remark1(a), the PD function of $X_{\mathcal{A}}$ aims at isolating the expected effect of $X_{\mathcal{A}}$ , when adjusting for potential influence from $X_{\mathcal{A}^{\mathrm{C}}}$ . This suggests to use of PD functions for covariate engineering w.r.t. individual covariates, which allows us to partition the covariate space and, ultimately, construct a data-driven categorical GLM. That is, if ${\mathrm{PD}}(x_j) \in B$ , we can construct the corresponding covariate set on the original covariate scale according to:

\begin{equation*} x_j \in \mathbb {B} \;:\!=\; \{x_j^* \in \mathbb {X}_j \;:\; {\mathrm {PD}}(x_j^*) \in B\}. \end{equation*}

This allows us to use the PD function to partition $\mathbb{X}_j$ , based on where $X_j$ is similar in terms of PD function values, which can be generalized to tuples of covariates.

In order to construct a partition based on PD functions, consider a sequence of $b_j^{(k)}$ s such that

(12) \begin{align} -\infty \le b_j^{(0)} \lt b_j^{(1)} \lt \ldots \lt b_j^{(\kappa - 1)} \lt b_j^{(\kappa )} \le + \infty, \end{align}

and set $B_j^{(k)} \;:\!=\; (b_j^{(k - 1)}, b_j^{(k)}]$ , i.e. $\cup _{k = 1}^\kappa B_j^{(k)} = \mathbb{R}$ . The corresponding partition of $\mathbb{X}_j$ , denoted $\Pi _j \;:\!=\; (\mathbb{B}_j^{(k)})_{k = 1}^\kappa$ , is defined in terms of the parts

(13) \begin{align} \mathbb{B}_j^{(k)} \;:\!=\; \{x_j^* \in \mathbb{X}_j \;:\; {\mathrm{PD}}(x_j^*) \in B_j^{(k)}\}, \, k = 1, \ldots, \kappa . \end{align}

That is, the pre-image of the PD function w.r.t. $B_j^{(k)}$ defines the corresponding covariate set $\mathbb{B}_j^{(k)}$ such that $\cup _{k = 1}^\kappa \mathbb{B}_j^{(k)} = \mathbb{X}_j$ . Thus, without having specified how to obtain a partition of the real line according to Equation (12), including both the size of the partition, $\kappa$ , and the location of split points, the $b_j^{(k)}$ s, it is clear that given such a partition the procedure outlined above can be used to construct a categorical GLM in agreement with Equation (3). Further, since the aim is to construct a categorical GLM with good predictive accuracy in terms of mean predictions, it is reasonable to only keep the parts in the partition $\Pi _j$ that actually impacts the response. In particular, note that

(14) \begin{align} \overline{\mu }_j^{(k)} \;:\!=\;{\mathbb{E}}[Y \mid X_j \in \mathbb{B}_j^{(k)}], \, k = 1, \ldots, \kappa, \end{align}

which allows us to introduce the following piece-wise constant mean predictor

(15) \begin{align} \overline{\mu }_j(X_j) \;:\!=\; \sum _{k = 1}^\kappa \overline{\mu }_j^{(k)}\textit{1}_{\{X_j \in \mathbb{B}_j^{(k)}\}}, \quad \overline{\mu }_j^{(k)} \in \mathbb{R}. \end{align}

In addition, note that if we assume that the $\overline{\mu }_j^{(k)}$ s is unique, which typically is the case, it holds that

(16) \begin{align} \{X_j(\omega ) \in \mathbb{B}_j^{(k)}\} = \{\overline{\mu }_j(X_j)(\omega ) = \overline{\mu }_j^{(k)}\}, \end{align}

together with

(17) \begin{align} \overline{\mu }_j(X_j) ={\mathbb{E}}[Y \mid \overline{\mu }_j(X_j)], \end{align}

where Equation (17) precisely corresponds to that $\overline{\mu }_j(X_j)$ is auto-calibrated (AC), see Krüger and Ziegel (Reference Krüger and Ziegel2021); Denuit et al. (Reference Denuit, Charpentier and Trufin2021). A consequence of this is that, given the information contained in $\overline{\mu }_j(X_j)$ , the predictor cannot be improved upon, and the predictor is both locally and globally unbiased. In particular, if we let $\widetilde{\overline{\mu }}_j(X_j)$ be a version of $\overline{\mu }_j(X_j)$ where a number of categories have been merged, i.e. the $\sigma$ -algebra generated by $\widetilde{\overline{\mu }}_j(X_j)$ is coarser than the one generated by $\overline{\mu }_j(X_j)$ , it holds that both ${\mathbb{E}}[Y \mid \overline{\mu }_j(X_j)]$ and ${\mathbb{E}}[Y \mid \widetilde{\overline{\mu }}_j(X_j)]$ are AC predictors, and ${\mathbb{E}}[Y \mid \overline{\mu }_j(X_j)]$ outperforms ${\mathbb{E}}[Y \mid \widetilde{\overline{\mu }}_j(X_j)]$ in terms of predictive performance, see Theorem 3.1 and Proposition 3.1 in Krüger and Ziegel (Reference Krüger and Ziegel2021). This, however, is a theoretical result, assuming access to an infinite amount of data. In practice, the $\overline \mu _j^{(k)}$ s are estimated using data and we only want to keep the $\overline \mu _j^{(k)}$ s that generalize well to unseen data. That is, those $\overline \mu _j^{(k)}$ s that do not generalize are merged, and from Equation (16), we know that merging of $\;\overline \mu _j^{(k)}$ s is equivalent to merging the corresponding parts in the covariate partition. Consequently, in order to find the most parsimonious covariate partition based on data, we will, in Section 3, introduce a procedure that combines Equation (17) with an out-of-sample loss minimization using cross-validation (CV). We refer to this as a marginal AC step.

This procedure is analogously defined for tuples of covariates, and a precise implementation is described in Section 3.

Remark 2.

1. (a) If we consider a numerical covariate, the idea of using a PD function to construct a covariate partition is only relevant when the PD function is not strictly monotone, since otherwise we could just as well partition the covariate directly based on, e.g., quantile values. Note that this comment applies to the procedure used in Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022) as well, and it applies if we would change from using PD functions to using, e.g., ALEs or other covariate effect measures. If the PD function would be monotone, but not strictly monotone, then the PD function of the underlying black-box predictor implies a coarsening of the covariate space.

   Further, from the above construction, it is clear that the PD function is only used to construct covariate partitions. That is, the actual impact on the response, here measured in terms of PD functions values, is of lesser importance, as long as the PD function changes when the covariate values change. Consequently, it is the sensitivity of the measure being used, here PD functions, that matters, not the level. The same comment, of course, applies if we use e.g. ALEs; for more on ALEs and PD functions, see Apley and Zhu (Reference Apley and Zhu2020) and Henckaerts et al. Reference Henckaerts, Antonio and Côté2022). Also, recall Remark 1(a) above.

2. (b) The output of (17) in the AC step is not a new PD function, but a conditional expected value. Still, the partitioning will be based on similarity in terms of PD function values, but those parts in the partition that do not affect the response will be removed. If one instead favor models with as high fidelity w.r.t. the original black-box predictor, i.e. a so-called surrogate model, see e.g. Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), the AC step is problematic for, e.g., ordered categories, since the merging of categories does not respect ordering. The corresponding step in the algorithm of Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), see their Algorithm1, merges categories only based on fidelity to the original PD function, see their Equation (2). Also note that for numerical and ordinal covariates the procedure in Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022) only merges PD function values that have adjacent covariate values.

3. Constructing a guided categorical GLM

The aim of the present note is to introduce a method of constructing a classical categorical GLM that is guided by a given black-box predictor. The main step is to define covariate partitions that define categorical versions of the initial covariates and interactions. Since the aim is to construct categorical covariates, the method will be applied to all initial covariates that are non-categorical.

The first step in creating a guided GLM is to calculate the PD function values from the external black-box predictor $\widehat \mu (x)$ . This needs to be done for each covariate dimension, and for all covariate tuples. We will start by focusing on single covariates, noting that tuples are handled analogously.

Next, in order to construct the covariate partitions for each covariate dimension $j$ , we need to the decide on the number of parts in the partition, $\kappa$ , together with the split points $b_j^{(k)}$ .

In the present note, we suggest doing this using $L^2$ -regression trees and CV. To see why this is reasonable, recall that an $L^2$ -regression tree can be represented as:

\begin{align*} T(x) \;:\!=\; \sum _{k = 1}^\kappa \delta _k \textit{1}_{\{x \in \mathbb{G}_k\}},\, \delta _k \in \mathbb{R}, \end{align*}

where $\cup _{k = 1}^\kappa \mathbb{G}_k \;=\!:\; \mathbb{X}$ , see e.g. (Hastie et al. Reference Hastie, Tibshirani and Friedman2009, Ch. 9), which is of the same form as $\overline{\mu }_j$ from Equation (15):

\begin{align*} \overline{\mu }_j(x_j) \;:\!=\; \sum _{k = 1}^\kappa \overline{\mu }_j^{(k)}\textit{1}_{\{x_j \in \mathbb{B}_j^{(k)}\}}. \end{align*}

Further, in this short note, we will use $L^2$ -regression trees estimated using square loss in a greedy manner, using CV, see e.g. (Hastie et al. Reference Hastie, Tibshirani and Friedman2009, Ch. 7). That is, the empirical loss that will be (greedily) minimized is given by:

(18) \begin{align} \widehat{\overline{\mu }}_j(x_j) \;:\!=\; \textrm{arg min}_{T \in \mathcal{T}_\kappa } \sum _{i = 1}^n w_i (y_i - T((x_j)_i))^2, \end{align}

where $(x_j)_i$ denotes the $i$ th observation of the $x_j$ th covariate, where the $w_i$ weights have been added in order to agree with the GLM assumptions from Equation (1), and where $\mathcal{T}_\kappa$ corresponds to the set of binary regression trees with at most $\kappa$ terminal nodes. Consequently, decreasing $\kappa$ corresponds to merging covariate regions $\mathbb{B}_j^{(k)}$ s, which is equivalent to coarsening the covariate partition, since the tree-based partition is defined recursively using binary splits. Moreover, note that due to Equation (13), the described tree-fitting procedure is equivalent to fitting an $L^2$ -regression tree using ${\mathrm{PD}}(x_j)$ as the single numerical covariate. As a consequence of this, the definition of the resulting $\mathbb{B}_j^{(k)}$ s will be implicitly defined in terms of the corresponding $\mathrm{PD}$ -function.

Furthermore, due to the relation (16), it is possible to extract a categorical covariate version of $x_j$ from the fitted predictor $\widehat{\overline{\mu }}_j(x_j)$ , which will take on at most $\kappa$ covariate values.

Continuing, the motivation for using $L^2$ -trees instead of, e.g., a Tweedie loss is because all Tweedie losses that are special cases of the Bregman deviance losses, see Denuit et al. (Reference Denuit, Charpentier and Trufin2021), result in the same mean predictor for a given part $\mathbb{B}_j^{(k)}$ in the partition, see e.g. Lindholm and Nazar (Reference Lindholm and Nazar2024). In particular, note that the resulting $\widehat{\overline{\mu }}_j$ s correspond to empirical means, regardless of the Tweedie loss function used. For alternatives to using $L^2$ -regression trees to achieve auto-calibration, see e.g. Denuit et al. (Reference Denuit, Charpentier and Trufin2021); Wüthrich and Ziegel (2023).

Consequently, by fitting $L^2$ -regression trees and using CV to decide on the optimal number of terminal nodes $\kappa ^*$ , where $1 \le \kappa ^* \le \kappa$ , which defines the coarseness of the partition, combines the search for suitable split points and a greedy coarsening of the covariate partition using auto-calibration into a single step. This corresponds to Step A in Algorithm1 describing the construction of a guided categorical GLM.

If the procedure from Section 2.2 is applied to all covariates and interactions, the resulting number of categorical levels, and, hence, $\beta$ coefficients to be estimated in Equation (3) can become very large. This suggests that regularization techniques should be used when fitting the final categorical GLM. One way of achieving this is to use $L^1$ -regularisation or so-called lasso-regularisation, see e.g. (Hastie et al. Reference Hastie, Tibshirani and Wainwright2015, Ch. 3). If we consider EDF models, this means that we, given the $\mathbb{B}_\bullet ^{(k)}$ s, use the following penalized deviance loss function:

(19) \begin{align} D(y;\; \beta, \lambda ) \;:\!=\; \sum _{i = 1}^n w_i d(y_i, \mu (x_i;\; \beta )) + \lambda |\beta |, \end{align}

which is the loss from Equation (4), but where the $L^1$ -penalty term $\lambda |\beta |$ has been added, where $\lambda$ is the penalty parameter. The $\lambda$ -parameter is chosen using $k$ -fold CV.

Moreover, if the covariate vector $x$ is high-dimensional, it can be demanding already to evaluate all two-way interactions fully. An alternative is here to consider only those two-way interactions that are believed to have an impact on the final model. This can be achieved by using Friedman’s $H$ statistic, see Friedman and Popescu (Reference Friedman and Popescu2008):

(20) \begin{align} H_{j, k} = \frac{\widehat{\mathbb{E}}[({\mathrm{PD}}(X_j, X_k) -{\mathrm{PD}}(X_j) -{\mathrm{PD}}(X_k))^2]}{\widehat{\mathbb{E}}[{\mathrm{PD}}(X_j, X_k)^2]}, \end{align}

where $\widehat{\mathbb{E}}[\cdot ]$ refers to the empirical expectation. That is, Equation (20) provides an estimate of the amount of excess variation in ${\mathrm{PD}}(X_j, X_k)$ compared with ${\mathrm{PD}}(X_j) +{\mathrm{PD}}(X_k)$ .

By combining all of the above, focusing on a categorical GLM with at most two-way interactions, we arrive at Algorithm1. Of course, if two-way interactions turn out to be insufficient, the procedure can be extended analogously to consider higher-order interactions as well.

Algorithm 1 – Guided GLM

4. Numerical illustrations

In the current section, we will construct guided categorical GLMs based on reference models that are GBMs, following the procedure described in Algorithm1, using the freMTPL, beMTPL, auspriv, and norauto data sets available in the R-package CASdataset, see Dutang and Charpentier (Reference Dutang and Charpentier2020). Only Poisson claim count models will be considered, i.e. the Poisson deviance

(21) \begin{align} D_{\mathrm{Pois}}(y;\; \mu ) \;:\!=\; \sum _{i = 1}^n w_i\left (y_i\log (y_i) - y_i\log (\mu _i) - y_i - \mu _i\right ), \end{align}

will be used for model estimation and prediction evaluation. Concerning data, for all data sets analyzed 2/3 of the data have been used for in-sample training, and 1/3 for out-of-sample (hold out) evaluation.

Further, all GBM models use a tree depth of two, 0.01 learning rate, and a bag fraction of 0.75 corresponding to the fraction of training data used for each tree iteration. The maximum number of trees is set to 4 000 with the optimal number chosen via 5-fold CV and the remaining hyperparameters are the default levels in the R-package GBM. Hence, hyperparameters for the GBM modeling are the same as those used in Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), as described in Section 3.2.1. The R-implementation used can be found at https://github.com/Johan246/Boosting-GLM.git

When implementing Algorithm1 the number of interaction terms is set to 5 ( $\gamma$ ) and the maximum size of the partition is set to 30 ( $\kappa$ ). Concerning the hyperparameters for the $L^2$ -trees ( $\theta _{tree}$ ), the minimum number of observations per node is set to 10 and the cost penalty parameter is set to 0.00001 in order to allow for very deep un-pruned trees, after which the optimal tree size, including pruning, is determined using CV as implemented according to the rpart-package in R.

As commented on in Remark3(2), the computational cost of calculating the PD function values for all observed covariates becomes infeasible. Due to this, all numerical covariates’ $\mathrm{PD}$ -functions are approximated as piece-wise constant step functions that only jump at $\kappa$ values corresponding to equidistant covariate percentile values.

Apart from the reference GBM model, the surrogate model from Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), maidrr, will be used for comparison and the R package with the same name is used in all numerical illustrations.

From Algorithm1, it is clear that there is no ambition to replicate the PD functions of the initial model, which here is a GBM. An example of PD functions for the different models for the freMTPL data is given in Fig. 1. From Fig. 1 it is also seen that the GBM’s PD functions are monotone for the covariates “Vehicle age” and “Bonus Malus,” but not strictly monotone. If these would have been strictly monotone, the covariates could have been adjusted directly using $L^2$ trees, see Remark2(a); as we can see from the GBM’s PD function plot, there are multiple covariate values having the same PD function value, which indicates that the GBM has introduced a coarsening of the covariate space. Moreover, from Fig. 1 it is also seen that the number of categories in the guided categorical GLM is reduced by using a final lasso ( $L^1$ ) step in Algorithm1. Further, the number of active parameters, i.e. non-zero $\beta$ regression coefficients in Equation (3), in the final guided categorical GLM are summarized in Table 1, and it can be noted that the number of parameters tends to be very low.

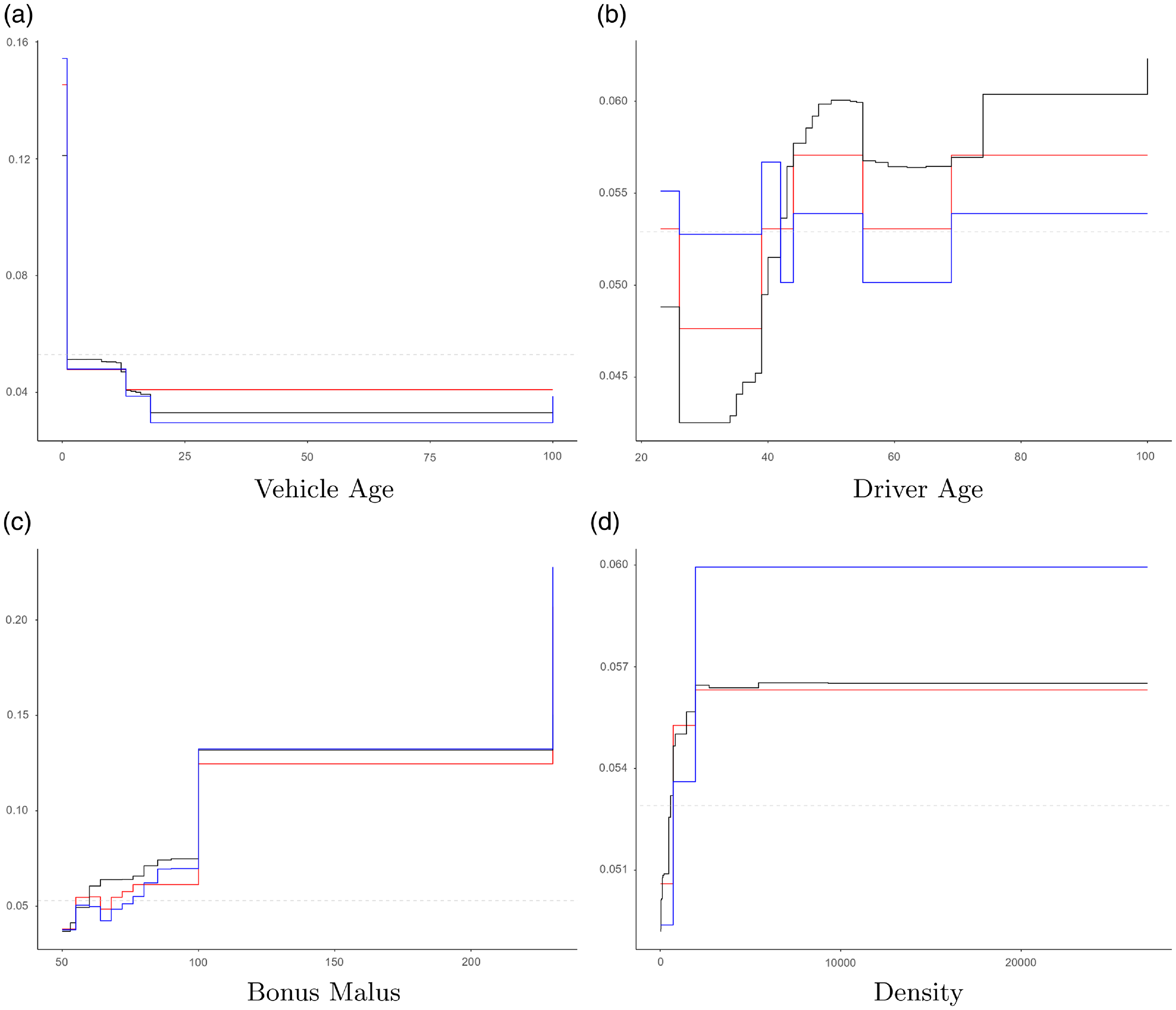
Figure 1 Comparison of model factor effects (partial dependence-function plots) for the freMTPL data between initial gradient boosting machine model (black lines), guided categorical generalized linear model including final lasso ( $L^1$ ) step (red lines), and a model including all levels found by the tree-calibration (blue lines).

Continuing, in order to compare the predictive performance of the guided categorical GLM and the reference GBM, we calculate the out-of-sample relative difference in Poisson deviance, $\Delta D_{\mathrm{Pois}}$ . The out-of-sample relative difference in Poisson deviance between the reference GBM and candidate model $\widehat \mu ^\star$ is defined according to:

(22) \begin{align} \Delta D_{\mathrm{Pois}} \;:\!=\; \frac{D_{\mathrm{Pois}}(y;\; \widehat \mu ^\star ) - D_{\mathrm{Pois}}(y;\; \widehat{\mu }^{\mathrm{GBM}})}{D_{\mathrm{Pois}}(y;\; \widehat{\mu }^{\mathrm{GBM}})}, \end{align}

where $D_{\mathrm{Pois}}(y;\; \mu )$ is given by Equation (21). From Table 1, it is seen that the $\Delta D_{\mathrm{Pois}}$ values for the different data sets are very small indicating that the guided categorical GLMs tend to track the performance of the initial GBMs closely. One can also note that the guided categorical GLM in fact outperforms the corresponding GBMs for the beMTPL and auspriv data sets, although these results could, at least partly, be due to random fluctuations. It is also worth highlighting that for both the auspriv and norauto data sets, a standard GLM without interactions outperforms the GBM in terms of Poisson deviance slightly, which is in agreement with that the guided GLM has a very low number of parameters. Further, in Table 1, the surrogate model from Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022) is included, denoted maidrr, which tends to be close to the guided GLM in terms of Poisson deviances, although slightly worse, with a generally higher fidelity to the reference GBM, as expected. Note, however, that these results are based on our own use of the maidrr R-package, which may be sub-optimally tuned, but the results obtained here seem close to the maidrr results from Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), see Table 4, and their relative Poisson deviances are comparable to those seen in Table 1 in this short note.

Moreover, the relative Poisson deviance values provide a summary of the overall out-of-sample performance. In order to assess local performance of the mean predictors, we use concentration curves, see Fig. 2, and for more concentration curves, we refer to e.g. Denuit et al. (Reference Denuit, Sznajder and Trufin2019). From Fig. 2, it is seen that also the local performance of the mean predictors of the guided categorical GLMs is comparable to the corresponding GBMs’ performance.

Concerning different covariates’ and interactions’ influence on the final predictor, recall that the final predictor is a regularized categorical GLM, and can hence be fitted using the glmnet package in R, and it is possible to use standard techniques such as variable importance plots (VIPs), see e.g. Greenwell et al. (Reference Greenwell, Boehmke and Gray2020). For a categorical GLM, the variable importance for a single covariate corresponds to the sum of the absolute values of the regression coefficients for its categories. This is illustrated in Fig. 3 for the different CASdataset data analyzed above. From Fig. 3, it is seen that there are a number of important categorical interaction terms for each model. This is information that is valuable when, e.g., constructing a tariff.

Table 1. Summary statistics for the different data sets, where $\Delta D_{\mathrm{Pois}}$ is defined in (22), and where fidelity refers to the correlation between the gradient boosting machine predictor and the corresponding candidate categorical generalized linear model (GLM) – the guided GLM or maidrr from Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022). The number of parameters refers to the guided GLM

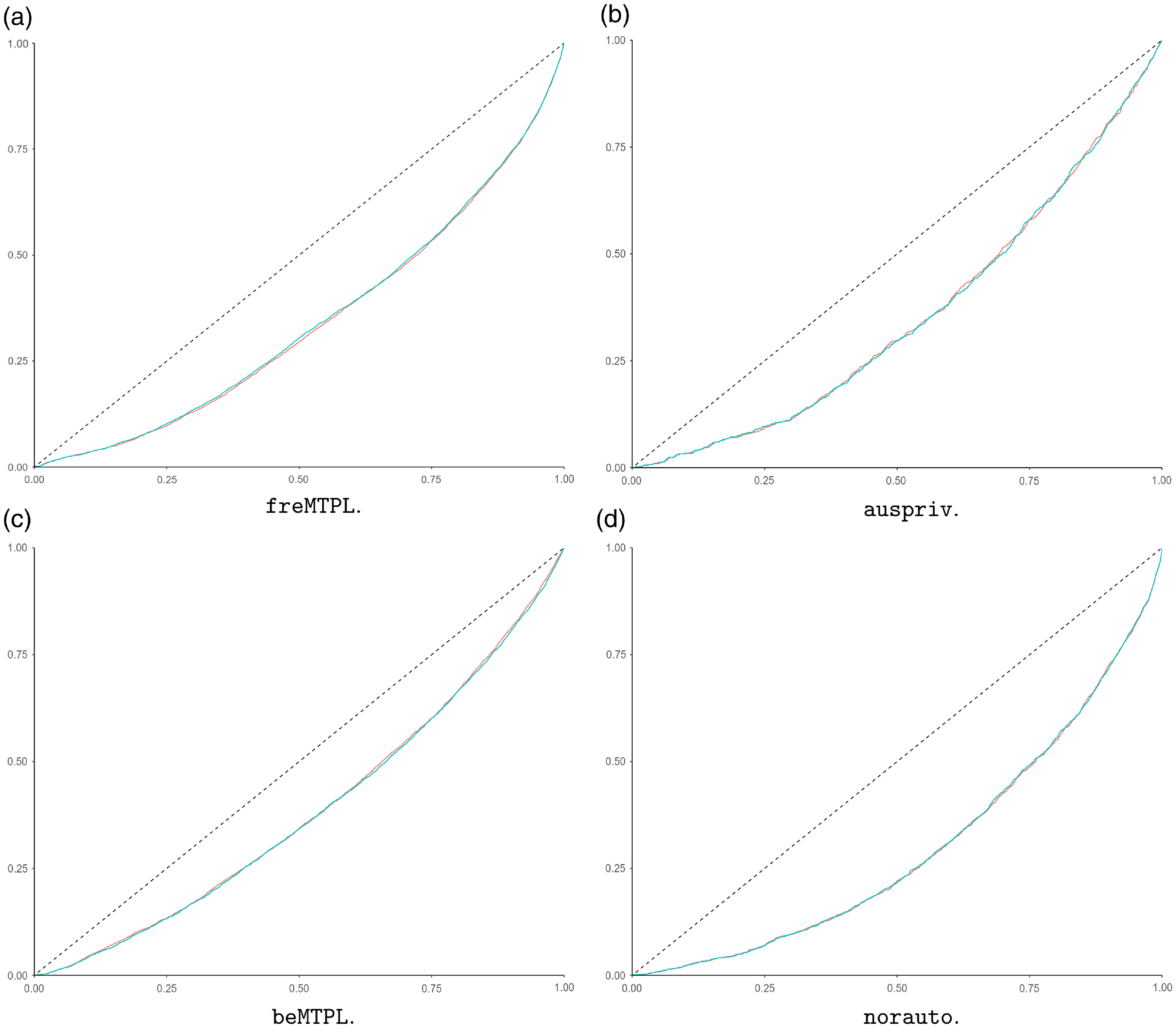
Figure 2 Concentration curves for different CASDatasets data comparing the original gradient boosting machine models (red lines) and the corresponding guided categorical generalized linear model (blue lines).

Figure 3 Variable importance plots for the final guided generalized linear model with lasso based on different CASDatasets data.

Further, VIPs provide a simple way to quantify global impact of covariates and interactions. Due to the categorical GLM structure, it is, however, straightforward to assess local impact by ranking the $\widehat \mu ^{\mathrm{GLM}^*}(x_i)$ s and inspect the contribution of individual covariates and interactions on the prediction. This is illustrated in Fig. 4, which shows $\exp \{\widehat \beta _j\}$ for specific covariate/interaction values corresponding to the 25%, 50%, and 75% percentiles of the empirical predictor distribution $(\widehat \mu (x_{i}))_i$ for different CASdataset data. Thus, from Fig. 4, we get a detailed picture of the importance of specific covariate/interaction values w.r.t. different risk percentiles. This is again valuable information for, e.g., constructing a tariff, but also for identifying characteristics of high-risk contracts.

Before ending this section, we briefly discuss surrogate aspects of the guided GLM. Table 1 shows the fidelity of the guided categorical GLM w.r.t. the original GBM model, where fidelity is defined as the correlation between the initial GBM mean predictor and the corresponding guided categorical GLM predictor. From this, it is seen that fidelity tends to be rather high for the data sets being analyzed, with no fidelity of less than 88%. These numbers, however, tend to deviate considerably for freMTPL and beMTPL compared to the surrogate model of Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022), see Table 5. This could, at least, partly be caused by the use of different seeds. It is, however, worth noting that the guided categorical GLMs with the lowest fidelity, beMTPL and freMTPL, are the ones that also differ the most compared with Henckaerts et al. (Reference Henckaerts, Antonio and Côté2022) w.r.t. predictive performance, in favor of the current guided GLM. Still, as commented on above, the observed differences could, at least partly, be due to not using the same seed.

A more detailed comparison of the original GBMs and the guided GLMs is provided by the scatter plots in Fig. 5, which agree with the fidelity calculations. The analogous scatter plots between the guided GLMs and the maidrr models look very similar to Fig. 5, but are slightly wider, and are not included.

Figure 4 Covariate contributions to the categorical generalized linear models (GLMs) mean predictor for different CASDatasets. From left to right: covariate contributions corresponding to the 25%, 50%, and 75% percentile of the empirical distribution of $(\widehat \mu (x_i))_i$ from the guided categorical GLM; each point corresponds to $\exp \{\widehat \beta _j\}$ for the particular covariate value/interaction term value. Note that interactions are represented without displaying a specific value on the $y$ -axes.

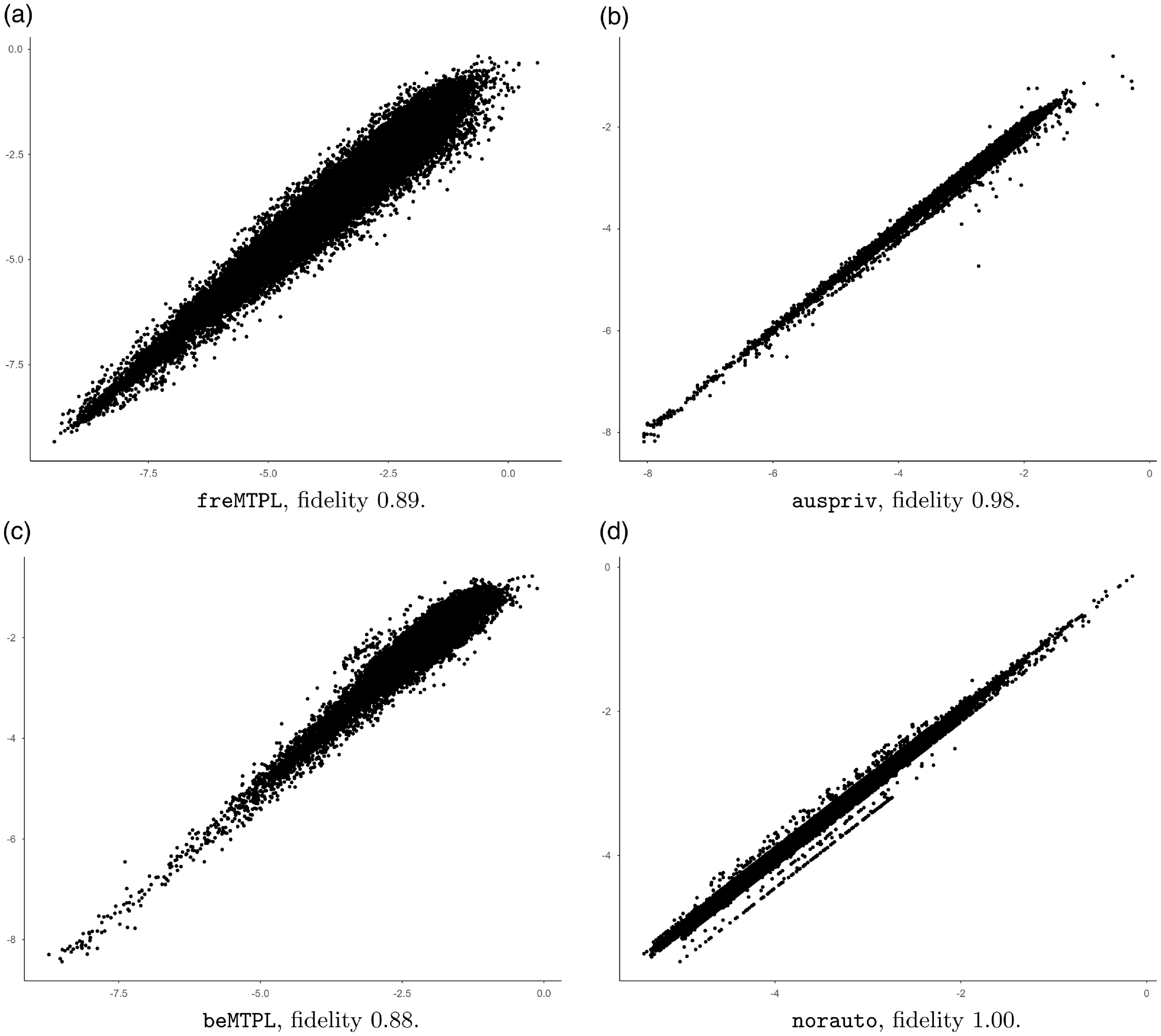
Figure 5 Scatter plots for different CASDatasets data on log-scale, comparing the original gradient boosting machine models ( $y$ -axes) and the corresponding guided categorical generalized linear models ( $x$ -axes) predictions. Fidelity corresponds to the correlation between the two predictors.