Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T18:27:42.397Z Has data issue: false hasContentIssue false
  • English
  • Français

On hazard rate ordering of dependent variables

Part of: Operations research and management science

Published online by Cambridge University Press:  01 July 2016

Emad-Eldin A. A. Aly  and
Subhash C. Kochar
Emad-Eldin A. A. Aly*
Affiliation:
University of Alberta
Subhash C. Kochar*
Affiliation:
Indian Statistical Institute, New Delhi
*
∗Postal address: Department of Statistics and Applied Probability, The University of Alberta, Edmonton, Alberta, Canada T6G 2G1.
∗∗Postal address: Indian Statistical Institute, 7, SJS Sansanwal Marg, New Delhi-110016, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Shanthikumar and Yao (1991) introduced some new stochastic order relations to compare the components of a bivariate random vector (X1, X2). As they point out in their paper, even if 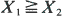according to their hazard rate (or likelihood ratio) ordering, the marginal distributions may not be ordered accordingly. We introduce some new concepts where the marginal distributions preserve the corresponding stochastic orders. Also a relation between the bivariate scale model and the introduced bivariate hazard rate ordering is established.

Keywords

CONDITIONAL HAZARD RATEBIVARIATE SCALE MODELSTOCHASTIC ORDERINGCAUSE SPECIFIC HAZARD RATEBIVARIATE INCREASING HAZARD RATE DISTRIBUTION

MSC classification

Primary: 90B35: Scheduling theory, deterministic
Type
Letters to the Editor
Information
Advances in Applied Probability , Volume 25 , Issue 2 , June 1993 , pp. 477 - 482
Copyright
Copyright © Applied Probability Trust 1993 

Footnotes

Research supported by an NSERC Canada grant at the University of Alberta.

Part of this research was done while visiting the University of Alberta supported by the NSERC Canada grant of the first author.

References

Barlow, R. E. and Proschan, F. (1981) Statistical Theory of Reliability and Life Testing. To Begin With, Silver Spring, Maryland.Google Scholar
Block, H. and Basu, A. P. (1974) A continuous bivariate exponential extension. J. Amer. Statist. Assoc. 69, 1031–1037.Google Scholar
Harris, R. (1970) A multivariate definition for hazard rate distributions. Ann. Math. Statist. 41, 413–417.Google Scholar
Kalbfleisch, J. D. and Prentice, R. L. (1980) The Statistical Analysis of Failure Time Data. Wiley, New York.Google Scholar
Keilson, J. and Sumita, U. (1982) Uniform stochastic ordering and related inequalities. Canad. J. Statist. 10, 181–198.Google Scholar
Kochar, S. C. (1979) Distribution-free comparison of two distributions with reference to their hazard rates. Biometrika 66, 437–441.Google Scholar
Righter, R. and Shanthikumar, J. G. (1992) Extension of the bivariate characterization for stochastic orders. Adv. Appl. Prob. 24, 506–508.CrossRefGoogle Scholar
Ross, S. (1983) Stochastic Processes. Wiley, New York.Google Scholar
Shaked, M. (1977) A family of concepts of dependence for bivariat distributions. J. Amer. Statist. Assoc. 72, 642–650.CrossRefGoogle Scholar
Shanthikumar, J. G. and Yao, D. D. (1991) Bivariate characterization of some stochastic order relations. Adv. Appl. Prob. 23, 642–659.Google Scholar