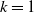1. Introduction
The extreme value theory of sequences of independent and identically distributed (i.i.d.) random variables has often been generalized to include the situation where the variables are no longer independent, as in the monograph of [Reference Leadbetter, Lindgren and Rootzén15], where for stationary processes the focus is on long-range dependence conditions and local clustering of extremes as measured by the extremal index. Among the most useful stochastic processes are positive recurrent Markov chains, with a continuous state space, which provide the backbone of a broad range of statistical models for stationary time series. Such models have attracted considerable interest in the analysis of extremes of stochastic processes. These processes meet the required long-range dependence conditions [Reference O’Brien19, Reference Rootzén27], so it is the local clustering properties of their extreme values that are of interest. By considering the behaviour of the process when it is extreme, that is, when it exceeds a high threshold, [Reference Rootzén27] showed that, under certain circumstances, the times of extreme events of stationary Markov chains that exceed a high threshold converge to a homogeneous Poisson process and that the limiting characteristics of the values within an extreme event, including the extremal index
![]() $\theta$
with
$\theta$
with
![]() $\theta\in (0,1]$
being the reciprocal of the mean extreme event duration, can be derived as the threshold converges to the upper endpoint of the marginal distribution. This limit result only reveals the behaviour of the process whilst it remains at the same level of marginal extremity as the threshold, and therefore it is only informative about the temporal structure of extreme events for a subset of processes, i.e. those with
$\theta\in (0,1]$
being the reciprocal of the mean extreme event duration, can be derived as the threshold converges to the upper endpoint of the marginal distribution. This limit result only reveals the behaviour of the process whilst it remains at the same level of marginal extremity as the threshold, and therefore it is only informative about the temporal structure of extreme events for a subset of processes, i.e. those with
![]() $\theta<1$
. This excludes all processes with
$\theta<1$
. This excludes all processes with
![]() $\theta=1$
, where extreme values occur in temporal isolation, with no apparent clustering of extreme values revealed through this limit theory. Processes with
$\theta=1$
, where extreme values occur in temporal isolation, with no apparent clustering of extreme values revealed through this limit theory. Processes with
![]() $\theta=1$
include all Gaussian processes, so they can exhibit strong temporal dependence. The behaviour of extreme events of these processes is of interest, but cannot be studied through the existing methods. So we are interested in deriving the detailed characteristics of a positive recurrent Markov chain within an extremal event, irrespective of whether
$\theta=1$
include all Gaussian processes, so they can exhibit strong temporal dependence. The behaviour of extreme events of these processes is of interest, but cannot be studied through the existing methods. So we are interested in deriving the detailed characteristics of a positive recurrent Markov chain within an extremal event, irrespective of whether
![]() $\theta<1$
or
$\theta<1$
or
![]() $\theta=1$
, to provide more insights than are currently available.
$\theta=1$
, to provide more insights than are currently available.
We focus on real-valued stationary kth-order Markov processes
![]() $\{X_t \,:\, t\in {{\mathbb{Z}}}\}$
, for
$\{X_t \,:\, t\in {{\mathbb{Z}}}\}$
, for
![]() $k\in{{\mathbb{N}}}$
, with the marginal distribution function F of
$k\in{{\mathbb{N}}}$
, with the marginal distribution function F of
![]() $X_t$
and with a copula [Reference Joe12] for the joint distributions of
$X_t$
and with a copula [Reference Joe12] for the joint distributions of
![]() $(X_{t-k}, \ldots , X_t)$
, for all
$(X_{t-k}, \ldots , X_t)$
, for all
![]() $t\in {{\mathbb{Z}}}$
, which is invariant to time, so that the one-step forward transition probability kernel
$t\in {{\mathbb{Z}}}$
, which is invariant to time, so that the one-step forward transition probability kernel
![]() $\pi$
is invariant to t, as it is a function of F and this copula. Motivated by the limitations of the established limit theory for stationary Markov chains, we seek to understand better the behaviour of such processes within an extreme event under less restrictive conditions, by using a more refined limit theory. Specifically, our analysis aims to characterize the temporal behaviour of extreme events transitioning between an extreme state and the body of the distribution irrespective of whether the process has
$\pi$
is invariant to t, as it is a function of F and this copula. Motivated by the limitations of the established limit theory for stationary Markov chains, we seek to understand better the behaviour of such processes within an extreme event under less restrictive conditions, by using a more refined limit theory. Specifically, our analysis aims to characterize the temporal behaviour of extreme events transitioning between an extreme state and the body of the distribution irrespective of whether the process has
![]() $\theta<1$
or
$\theta<1$
or
![]() $\theta=1$
.
$\theta=1$
.
The case where
![]() $k=1$
has been well studied. Under weak conditions, [Reference Rootzén27, Reference Smith31] show that the powerful general Poisson limit gives that the extremal index is either
$k=1$
has been well studied. Under weak conditions, [Reference Rootzén27, Reference Smith31] show that the powerful general Poisson limit gives that the extremal index is either
![]() $\theta<1$
or
$\theta<1$
or
![]() $\theta=1$
, respectively, depending on whether
$\theta=1$
, respectively, depending on whether
![]() $\chi_1>0$
or
$\chi_1>0$
or
![]() $\chi_1=0$
, where
$\chi_1=0$
, where
for all
![]() $t\in {{\mathbb{Z}}}$
. These two limiting properties are known as asymptotic dependence and asymptotic independence of
$t\in {{\mathbb{Z}}}$
. These two limiting properties are known as asymptotic dependence and asymptotic independence of
![]() $(X_{t-1},X_t)$
, respectively, in the literature on bivariate extremes. To derive greater detail about the behaviour within extreme events for asymptotically dependent Markov chains, the appropriate strategy is to study tail chains [Reference Janßen and Segers11]. A tail chain arises as a limiting process after witnessing an extreme state, under rescaling of the future Markov chain by the value of the process in the extreme state, resulting in the tail chain being driven by a random walk. Tail chains fail to reveal the detailed structure of extreme events for any asymptotically independent process. For
$(X_{t-1},X_t)$
, respectively, in the literature on bivariate extremes. To derive greater detail about the behaviour within extreme events for asymptotically dependent Markov chains, the appropriate strategy is to study tail chains [Reference Janßen and Segers11]. A tail chain arises as a limiting process after witnessing an extreme state, under rescaling of the future Markov chain by the value of the process in the extreme state, resulting in the tail chain being driven by a random walk. Tail chains fail to reveal the detailed structure of extreme events for any asymptotically independent process. For
![]() $k=1$
, [Reference Papastathopoulos, Strokorb, Tawn and Butler20] take a different approach, using a new limiting theory involving hidden tail chains, defined below by the limit (2), which treat both asymptotically dependent and asymptotically independent chains in a unified theory. They establish the extremal event properties that we require more generally for when
$k=1$
, [Reference Papastathopoulos, Strokorb, Tawn and Butler20] take a different approach, using a new limiting theory involving hidden tail chains, defined below by the limit (2), which treat both asymptotically dependent and asymptotically independent chains in a unified theory. They establish the extremal event properties that we require more generally for when
![]() $k>1$
. So the focus of our paper is similar to that of [Reference Papastathopoulos, Strokorb, Tawn and Butler20], but with the added difficulty that the complexity of extreme events substantially increases with k.
$k>1$
. So the focus of our paper is similar to that of [Reference Papastathopoulos, Strokorb, Tawn and Butler20], but with the added difficulty that the complexity of extreme events substantially increases with k.
Markov processes with order
![]() $k>1$
extend the traditional concept of first-order Markov processes by incorporating information from the
$k>1$
extend the traditional concept of first-order Markov processes by incorporating information from the
![]() $k\in{{\mathbb{N}}}$
most recent states into the transition behaviour of the next state. The fundamental importance of these higher-order Markov processes lies in their ability to capture and model dependencies in time-series data in real-world scenarios, which first-order Markov processes would fail to do. Specifically, the first-order process can account only for the current level of the process and not whether at that time the process has just moved up or down;
$k\in{{\mathbb{N}}}$
most recent states into the transition behaviour of the next state. The fundamental importance of these higher-order Markov processes lies in their ability to capture and model dependencies in time-series data in real-world scenarios, which first-order Markov processes would fail to do. Specifically, the first-order process can account only for the current level of the process and not whether at that time the process has just moved up or down;
![]() $k=2$
is required in such a scenario, with larger k needed as more subtle memory of the past is important to determine the future behaviour. To the best of our knowledge, key characteristics of the extremal behaviour of higher-order Markov chains have not been dealt with in depth, yet these are crucial for understanding the evolution of extreme events of random processes and for providing well-founded parametric models that can be used for inference, prediction, and assessment of risk, e.g. [Reference Winter and Tawn36, Reference Winter and Tawn37].
$k=2$
is required in such a scenario, with larger k needed as more subtle memory of the past is important to determine the future behaviour. To the best of our knowledge, key characteristics of the extremal behaviour of higher-order Markov chains have not been dealt with in depth, yet these are crucial for understanding the evolution of extreme events of random processes and for providing well-founded parametric models that can be used for inference, prediction, and assessment of risk, e.g. [Reference Winter and Tawn36, Reference Winter and Tawn37].
Modelling stationary kth-order Markov processes requires the modelling of
![]() $(k+1)$
-dimensional multivariate distributions of
$(k+1)$
-dimensional multivariate distributions of
![]() $(X_{t-k}, \ldots ,X_t)$
to describe the transition distributions
$(X_{t-k}, \ldots ,X_t)$
to describe the transition distributions
![]() $\pi$
of
$\pi$
of
![]() $X_t\,\mid\,(X_{t-1}, \ldots ,X_{t-k})$
, so the extremal properties of these processes cannot be characterized as simply as by the measure
$X_t\,\mid\,(X_{t-1}, \ldots ,X_{t-k})$
, so the extremal properties of these processes cannot be characterized as simply as by the measure
![]() $\chi_1$
. In fact, it is known from multivariate extreme-value theory that the challenge grows exponentially with k [Reference Chiapino, Sabourin and Segers3, Reference Simpson, Wadsworth and Tawn30]. [Reference Janßen and Segers11, Reference Resnick and Zeber26] work on tail chains when
$\chi_1$
. In fact, it is known from multivariate extreme-value theory that the challenge grows exponentially with k [Reference Chiapino, Sabourin and Segers3, Reference Simpson, Wadsworth and Tawn30]. [Reference Janßen and Segers11, Reference Resnick and Zeber26] work on tail chains when
![]() $k>1$
, but restrict themselves to processes which, in addition to other conditions, require that
$k>1$
, but restrict themselves to processes which, in addition to other conditions, require that
![]() $\chi_j>0$
for all
$\chi_j>0$
for all
![]() $j=1, \ldots ,k$
, where
$j=1, \ldots ,k$
, where
for all
![]() $t\in {{\mathbb{Z}}}$
(which is termed full pairwise asymptotic dependence across all variables in the transition), and restrict the Markov chain from moving from an extreme state to the body of the process in a single step. Even in these restrictive cases few results exist, e.g. [Reference Janßen and Segers11, Reference Perfekt23, Reference Yun39]; however, we provide some extensions of these. We also derive the extensive extremal properties for full pairwise asymptotically independent processes, i.e. with
$t\in {{\mathbb{Z}}}$
(which is termed full pairwise asymptotic dependence across all variables in the transition), and restrict the Markov chain from moving from an extreme state to the body of the process in a single step. Even in these restrictive cases few results exist, e.g. [Reference Janßen and Segers11, Reference Perfekt23, Reference Yun39]; however, we provide some extensions of these. We also derive the extensive extremal properties for full pairwise asymptotically independent processes, i.e. with
![]() $\chi_j=0$
for
$\chi_j=0$
for
![]() $j=1,\ldots ,k-1$
. Finally, we determine the behaviour for extreme events for a class of processes which allow a subset of the
$j=1,\ldots ,k-1$
. Finally, we determine the behaviour for extreme events for a class of processes which allow a subset of the
![]() $k>1$
consecutive states to be in the body of the process while the rest are in an extreme state. This class of process falls between previous investigations and our core developments here.
$k>1$
consecutive states to be in the body of the process while the rest are in an extreme state. This class of process falls between previous investigations and our core developments here.
To work with hidden tail chains, we study the effect of different dependence structures for stationary Markov chains with marginal distributions with exponential tails, for which [Reference Papastathopoulos, Strokorb, Tawn and Butler20] show that more general results can be achieved when
![]() $k=1$
when using affine normalizations than when the marginals have regularly varying tails, which is the assumption typically used in studying tail chains. There is no loss of generality in making such a transform, as through the probability integral transform we can transform from any marginal distribution to any other, e.g. from regularly varying tails to being in the Gumbel max-domain of attraction.
$k=1$
when using affine normalizations than when the marginals have regularly varying tails, which is the assumption typically used in studying tail chains. There is no loss of generality in making such a transform, as through the probability integral transform we can transform from any marginal distribution to any other, e.g. from regularly varying tails to being in the Gumbel max-domain of attraction.
Without loss of generality, we assume that
![]() $\sup\{x \,:\, F(x) < 1\}=\infty$
. For
$\sup\{x \,:\, F(x) < 1\}=\infty$
. For
![]() $k>1$
, we assume that there exist
$k>1$
, we assume that there exist
![]() $k-1$
norming functions
$k-1$
norming functions
![]() $a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
$a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
![]() $b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, for
$b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, for
![]() $t=1,\ldots, k-1$
, such that
$t=1,\ldots, k-1$
, such that
as
![]() $u\to \infty$
, where
$u\to \infty$
, where
![]() ${{\,\overset {d }{\longrightarrow }\,}}$
denotes convergence in distribution and
${{\,\overset {d }{\longrightarrow }\,}}$
denotes convergence in distribution and
![]() $({{Z}}_1,\ldots, {{Z}}_{k-1})$
is a random vector that is non-degenerate in each component. Then our aim is to find conditions that guarantee the existence of an infinite sequence of additional functions
$({{Z}}_1,\ldots, {{Z}}_{k-1})$
is a random vector that is non-degenerate in each component. Then our aim is to find conditions that guarantee the existence of an infinite sequence of additional functions
![]() $a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
$a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
![]() $b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
for
$b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
for
![]() $t=k,k+1,\ldots$
, such that
$t=k,k+1,\ldots$
, such that
where each
![]() ${{Z}}_t$
is non-degenerate, with the limit process
${{Z}}_t$
is non-degenerate, with the limit process
![]() $\{{{Z}}_t\,:\,t=1,2,\ldots\}$
termed the hidden tail chain. The hidden tail chain generalizes the tail chain studied by [Reference Janßen and Segers11], as with our marginal choice, the tail chains require norming functions to be
$\{{{Z}}_t\,:\,t=1,2,\ldots\}$
termed the hidden tail chain. The hidden tail chain generalizes the tail chain studied by [Reference Janßen and Segers11], as with our marginal choice, the tail chains require norming functions to be
![]() $a_t(x)=x$
and
$a_t(x)=x$
and
![]() $b_t(x)=1$
for all t, and any
$b_t(x)=1$
for all t, and any
![]() ${{Z}}_t$
can be degenerate at
${{Z}}_t$
can be degenerate at
![]() $\{-\infty\}$
. In cases where we find that
$\{-\infty\}$
. In cases where we find that
![]() $a_t(x)/x\to \alpha_t < 1$
as
$a_t(x)/x\to \alpha_t < 1$
as
![]() $x\to \infty$
for all
$x\to \infty$
for all
![]() $t=1,2,\ldots ,k-1$
(that is, as [Reference Heffernan and Tawn9] show, the process has asymptotic pairwise independence for all lags up to
$t=1,2,\ldots ,k-1$
(that is, as [Reference Heffernan and Tawn9] show, the process has asymptotic pairwise independence for all lags up to
![]() $k-1$
), the tail chain degenerates as
$k-1$
), the tail chain degenerates as
![]() $\{-\infty, -\infty, \ldots\}$
but the hidden tail chain is non-degenerate and stochastic for all components. Furthermore, we find that if the process is asymptotically dependent for all lags
$\{-\infty, -\infty, \ldots\}$
but the hidden tail chain is non-degenerate and stochastic for all components. Furthermore, we find that if the process is asymptotically dependent for all lags
![]() $t=1, \ldots ,k-1$
, i.e.
$t=1, \ldots ,k-1$
, i.e.
![]() $a_t(x) \sim x$
and
$a_t(x) \sim x$
and
![]() $b_t(x)\sim 1$
as
$b_t(x)\sim 1$
as
![]() $x\to \infty$
for all
$x\to \infty$
for all
![]() $t=1,2,\ldots ,k-1$
, then the hidden tail chain is identical to the tail chain. So the hidden tail chain reveals important structure of the extreme events lost by the tail chain when the tail chain becomes degenerate, but it equals the tail chain otherwise. Thus hidden tail chains have wider use than tail chains.
$t=1,2,\ldots ,k-1$
, then the hidden tail chain is identical to the tail chain. So the hidden tail chain reveals important structure of the extreme events lost by the tail chain when the tail chain becomes degenerate, but it equals the tail chain otherwise. Thus hidden tail chains have wider use than tail chains.
Our primary targets are, under weak conditions, to find how the first
![]() $k-1$
norming functions
$k-1$
norming functions
![]() $a_t(\cdot)$
and
$a_t(\cdot)$
and
![]() $b_t(\cdot)$
in the limit (1) control those in the limit (2), where
$b_t(\cdot)$
in the limit (1) control those in the limit (2), where
![]() $t\geq k$
, and to identify the transition dynamics of the hidden tail chain along its index and across its state space. For the former, to find the behaviour of the
$t\geq k$
, and to identify the transition dynamics of the hidden tail chain along its index and across its state space. For the former, to find the behaviour of the
![]() $t\ge k$
norming functions requires a step-change in approach relative to the case when
$t\ge k$
norming functions requires a step-change in approach relative to the case when
![]() $k=1$
, studied by [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. In particular, the transitions involve novel functions, a and b, of the k previous values, in comparison to just the single value when
$k=1$
, studied by [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. In particular, the transitions involve novel functions, a and b, of the k previous values, in comparison to just the single value when
![]() $k=1$
. This instantly makes the problem more challenging, as not only do the transition functions have more arguments, but there can be interaction effects from these arguments. Here we develop results for determining the form of this class of functions and present a method of deriving them in applications. We find some parallels between the extremal properties of the norming functions and the Yule–Walker equations, used in standard time-series analysis [Reference Walker35, Reference Yule38]. We also make the surprising finding that we can always express the hidden tail chain in the form of a non-stationary scaled autoregressive process. Specifically,
$k=1$
. This instantly makes the problem more challenging, as not only do the transition functions have more arguments, but there can be interaction effects from these arguments. Here we develop results for determining the form of this class of functions and present a method of deriving them in applications. We find some parallels between the extremal properties of the norming functions and the Yule–Walker equations, used in standard time-series analysis [Reference Walker35, Reference Yule38]. We also make the surprising finding that we can always express the hidden tail chain in the form of a non-stationary scaled autoregressive process. Specifically,
where
![]() ${\boldsymbol{Z}}_{t-k\,:\,t-1}=({{Z}}_{t-k},\ldots, {{Z}}_{t-1})$
,
${\boldsymbol{Z}}_{t-k\,:\,t-1}=({{Z}}_{t-k},\ldots, {{Z}}_{t-1})$
,
![]() $\psi^a_{{{t}}}\,:\, {{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
$\psi^a_{{{t}}}\,:\, {{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
![]() $\psi^b_{{{t}}}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
are continuous update functions which fall in a particular class of functions, and
$\psi^b_{{{t}}}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
are continuous update functions which fall in a particular class of functions, and
![]() $\{ {{\varepsilon}}_{{{t}}} \,:\, t=1,2,\ldots \}$
is a sequence of non-degenerate i.i.d. innovations.
$\{ {{\varepsilon}}_{{{t}}} \,:\, t=1,2,\ldots \}$
is a sequence of non-degenerate i.i.d. innovations.
Using the values of
![]() $a_t,b_t$
and the properties of
$a_t,b_t$
and the properties of
![]() $Z_t$
, as
$Z_t$
, as
![]() $t\rightarrow \infty$
, we are able to investigate how the Markov chain returns to a non-extreme state following the occurrence of an extreme state. We focus almost exclusively on forward-in-time hidden tail chains, as in the limit (1), but we also briefly discuss back-and-forth hidden tail chains, expanding on the equivalent feature for tail chains that [Reference Janßen and Segers11] study. The limit theory developed in this paper is the first that considers asymptotic independence when studying extreme values of any structured process other than a first-order Markov processes. The extension to stationary kth-order Markov processes opens up the possibility of developing similar theory for much broader classes of graphical models. The study of multivariate extreme values on graphical structures has been a rich vein of research recently, with several influential papers, such as [Reference Asenova and Segers1, Reference Engelke and Hitz5, Reference Engelke and Ivanovs6, Reference Segers29]. However, all of these papers focus on the case in which all underlying distributions of cliques on the graph are asymptotically dependent. We believe that the results in this paper will help to unlock these approaches to enable the case when some, or all, cliques have asymptotic independence.
$t\rightarrow \infty$
, we are able to investigate how the Markov chain returns to a non-extreme state following the occurrence of an extreme state. We focus almost exclusively on forward-in-time hidden tail chains, as in the limit (1), but we also briefly discuss back-and-forth hidden tail chains, expanding on the equivalent feature for tail chains that [Reference Janßen and Segers11] study. The limit theory developed in this paper is the first that considers asymptotic independence when studying extreme values of any structured process other than a first-order Markov processes. The extension to stationary kth-order Markov processes opens up the possibility of developing similar theory for much broader classes of graphical models. The study of multivariate extreme values on graphical structures has been a rich vein of research recently, with several influential papers, such as [Reference Asenova and Segers1, Reference Engelke and Hitz5, Reference Engelke and Ivanovs6, Reference Segers29]. However, all of these papers focus on the case in which all underlying distributions of cliques on the graph are asymptotically dependent. We believe that the results in this paper will help to unlock these approaches to enable the case when some, or all, cliques have asymptotic independence.
Organization of the paper. In Section 2, we state our main theoretical results for higher-order Markov chains with affine update functions under rather broad assumptions. In particular, in that section we relax the requirement for the Markov chain to be stationary, instead assuming only that it is homogeneous. This allows us to show that the new developments here apply more generally. However, from Section 3 onwards we restrict attention to stationary processes, as they allow for the derivation of a much a more refined characterization of extreme events and enable comparisons with past literature. Specifically, in Section 3 we study hidden tail chains of full pairwise asymptotically dependent and full pairwise asymptotically independent stationary Markov chains with standardized marginal distributions. Based on the theory established in Sections 2 and 3 we study a number of special cases and obtain either simpler or closed-form solutions in Sections 4 and 5. Specifically, in Section 4 we characterize closed-form solutions for the norming functions for a class of asymptotically independent Markov chains, with the structure of these functions paralleling that of the autocovariance in Yule–Walker equations. In Section 5, we provide examples of Markov chains constructed from widely studied classes of joint distributions, such as Gaussian, max-stable, and inverted max-stable copulas, and provide a detailed analysis for particular parametric sub-families of these classes. All proofs are postponed to Appendix A.
Some notation. We use the following notation linked to vector and multivariate function operations. Vectors are typeset in bold and vector algebra is interpreted as componentwise throughout the paper. For example, when
![]() ${\boldsymbol{x}}=(x_1, \ldots ,x_k)$
and
${\boldsymbol{x}}=(x_1, \ldots ,x_k)$
and
![]() ${\boldsymbol{x}}^{\prime}=(x^{\prime}_1, \ldots ,x^{\prime}_k)$
are two vectors of the same size,
${\boldsymbol{x}}^{\prime}=(x^{\prime}_1, \ldots ,x^{\prime}_k)$
are two vectors of the same size,
![]() ${\boldsymbol{x}}/{\boldsymbol{x}}^{\prime} = (x_1/x^{\prime}_1, \ldots , x_k/x^{\prime}_k)$
. We also use
${\boldsymbol{x}}/{\boldsymbol{x}}^{\prime} = (x_1/x^{\prime}_1, \ldots , x_k/x^{\prime}_k)$
. We also use
![]() $d {\boldsymbol{x}}_{0\,:\,t}$
as shorthand for
$d {\boldsymbol{x}}_{0\,:\,t}$
as shorthand for
![]() $ d x_0\times\cdots\times d x_{t}$
. The notation
$ d x_0\times\cdots\times d x_{t}$
. The notation
![]() ${\boldsymbol{x}}^\top {\boldsymbol{y}}$
is reserved for the scalar product of two vectors
${\boldsymbol{x}}^\top {\boldsymbol{y}}$
is reserved for the scalar product of two vectors
![]() ${\boldsymbol{x}}, {\boldsymbol{y}}\in {{{\mathbb{R}}}}^k$
, that is,
${\boldsymbol{x}}, {\boldsymbol{y}}\in {{{\mathbb{R}}}}^k$
, that is,
![]() ${\boldsymbol{x}}^\top {\boldsymbol{y}} = \sum_{i=1}^kx_i \,y_i$
. For a sequence of measurable functions
${\boldsymbol{x}}^\top {\boldsymbol{y}} = \sum_{i=1}^kx_i \,y_i$
. For a sequence of measurable functions
![]() $\{g_t\}_{t \in {{\mathbb{N}}}}$
and real numbers
$\{g_t\}_{t \in {{\mathbb{N}}}}$
and real numbers
![]() $\{x_t\}_{t \in {{\mathbb{N}}}}$
, the notation
$\{x_t\}_{t \in {{\mathbb{N}}}}$
, the notation
![]() ${\boldsymbol{g}}_{t-k\,:\,t-1}(x)$
and
${\boldsymbol{g}}_{t-k\,:\,t-1}(x)$
and
![]() ${\boldsymbol{x}}_{t-k\,:\,t-1}$
, for
${\boldsymbol{x}}_{t-k\,:\,t-1}$
, for
![]() $t,k,t-k\in {{\mathbb{N}}}$
, is used to denote
$t,k,t-k\in {{\mathbb{N}}}$
, is used to denote
![]() $(g_{t-k}(x),\ldots,g_{t-1}(x))$
and
$(g_{t-k}(x),\ldots,g_{t-1}(x))$
and
![]() $(x_{t-k},\ldots,x_{t-1})$
, respectively. By convention, univariable functions on vectors are applied componentwise; e.g. if
$(x_{t-k},\ldots,x_{t-1})$
, respectively. By convention, univariable functions on vectors are applied componentwise; e.g. if
![]() $f \,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}$
,
$f \,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}$
,
![]() ${\boldsymbol{x}} \in {{{\mathbb{R}}}}^k$
, then
${\boldsymbol{x}} \in {{{\mathbb{R}}}}^k$
, then
![]() $f ({\boldsymbol{x}}) = (f (x_1), \ldots, f (x_k))$
. The symbols
$f ({\boldsymbol{x}}) = (f (x_1), \ldots, f (x_k))$
. The symbols
![]() ${\textbf{0}}_p$
and
${\textbf{0}}_p$
and
![]() ${\textbf{1}}_p$
, where
${\textbf{1}}_p$
, where
![]() $p \in {{\mathbb{N}}}$
, are used to denote the vectors
$p \in {{\mathbb{N}}}$
, are used to denote the vectors
![]() $(0,\ldots,0) \in {{{\mathbb{R}}}}^p$
and
$(0,\ldots,0) \in {{{\mathbb{R}}}}^p$
and
![]() $(1,\ldots,1)\in{{{\mathbb{R}}}}^p$
. We use the notation
$(1,\ldots,1)\in{{{\mathbb{R}}}}^p$
. We use the notation
![]() $\lVert {\boldsymbol{x}} \lVert $
for the
$\lVert {\boldsymbol{x}} \lVert $
for the
![]() $L_1$
norm of a k-dimensional vector
$L_1$
norm of a k-dimensional vector
![]() ${\boldsymbol{x}}$
. For a Cartesian coordinate system
${\boldsymbol{x}}$
. For a Cartesian coordinate system
![]() ${{{\mathbb{R}}}}^k$
with coordinates
${{{\mathbb{R}}}}^k$
with coordinates
![]() $x_1,\ldots,x_{k}$
,
$x_1,\ldots,x_{k}$
,
![]() $\nabla$
is defined by the partial derivative operators as
$\nabla$
is defined by the partial derivative operators as
![]() $\nabla=\sum_{i=1}^k (\partial/\partial x_i) {\boldsymbol{e}}_i$
for an orthonormal basis
$\nabla=\sum_{i=1}^k (\partial/\partial x_i) {\boldsymbol{e}}_i$
for an orthonormal basis
![]() $\{{\boldsymbol{e}}_1, \ldots, {\boldsymbol{e}}_k\}$
. The gradient vector of a differentiable function
$\{{\boldsymbol{e}}_1, \ldots, {\boldsymbol{e}}_k\}$
. The gradient vector of a differentiable function
![]() $f\,:\,{{{\mathbb{R}}}}^k\rightarrow {{{\mathbb{R}}}}$
at
$f\,:\,{{{\mathbb{R}}}}^k\rightarrow {{{\mathbb{R}}}}$
at
![]() ${\boldsymbol{x}}$
is denoted by
${\boldsymbol{x}}$
is denoted by
![]() $\nabla f({\boldsymbol{x}})=((\nabla f)_1({\boldsymbol{x}}),\ldots, (\nabla f)_k({\boldsymbol{x}}))$
.
$\nabla f({\boldsymbol{x}})=((\nabla f)_1({\boldsymbol{x}}),\ldots, (\nabla f)_k({\boldsymbol{x}}))$
.
We use the following notation for sets and special functions. The closure of a set A is denoted by
![]() $\overline{A}$
. The
$\overline{A}$
. The
![]() $(k-1)$
-dimensional unit simplex
$(k-1)$
-dimensional unit simplex
![]() $\{\boldsymbol{\omega} \in [0,\infty)^k\,:\, \lVert\boldsymbol{\omega} \lVert =1\}$
,
$\{\boldsymbol{\omega} \in [0,\infty)^k\,:\, \lVert\boldsymbol{\omega} \lVert =1\}$
,
![]() $k\in {{\mathbb{N}}}$
, is denoted by
$k\in {{\mathbb{N}}}$
, is denoted by
![]() ${{\Delta}}^{k-1}$
. Given cones
${{\Delta}}^{k-1}$
. Given cones
![]() $\mathcal{K}\subseteq {{{\mathbb{R}}}}_+^k$
and
$\mathcal{K}\subseteq {{{\mathbb{R}}}}_+^k$
and
![]() $\mathcal{K}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
, a function
$\mathcal{K}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
, a function
![]() $f\,:\,\mathcal{K} \to \mathcal{K}^{\prime}$
is called homogeneous of degree
$f\,:\,\mathcal{K} \to \mathcal{K}^{\prime}$
is called homogeneous of degree
![]() $\rho\in{{{\mathbb{R}}}}$
if
$\rho\in{{{\mathbb{R}}}}$
if
![]() $f(\lambda {\boldsymbol{x}})= \lambda^\rho f({\boldsymbol{x}})$
for all
$f(\lambda {\boldsymbol{x}})= \lambda^\rho f({\boldsymbol{x}})$
for all
![]() ${\boldsymbol{x}}\in\mathcal{K}$
and
${\boldsymbol{x}}\in\mathcal{K}$
and
![]() $\lambda>0$
. Given cones
$\lambda>0$
. Given cones
![]() $\mathcal{K}\subseteq {{{\mathbb{R}}}}_+^k$
and
$\mathcal{K}\subseteq {{{\mathbb{R}}}}_+^k$
and
![]() $\mathcal{K}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
, a map
$\mathcal{K}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
, a map
![]() $f\,:\,\mathcal{X}\to \mathcal{X}^{\prime}$
with
$f\,:\,\mathcal{X}\to \mathcal{X}^{\prime}$
with
![]() $\mathcal{X}\subseteq {{{\mathbb{R}}}}_+^k$
and
$\mathcal{X}\subseteq {{{\mathbb{R}}}}_+^k$
and
![]() $\mathcal{X}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
is said to be order-preserving if
$\mathcal{X}^{\prime}\subseteq {{{\mathbb{R}}}}_+^k$
is said to be order-preserving if
![]() ${\boldsymbol{y}}-{\boldsymbol{x}} \in \mathcal{K}$
implies
${\boldsymbol{y}}-{\boldsymbol{x}} \in \mathcal{K}$
implies
![]() $f({\boldsymbol{y}})-f({\boldsymbol{x}})\in \mathcal{K}^{\prime}$
. An identity map, denoted by
$f({\boldsymbol{y}})-f({\boldsymbol{x}})\in \mathcal{K}^{\prime}$
. An identity map, denoted by
![]() $\text{id}\,:\, \mathcal{X}\to \mathcal{X}$
, takes every element in a set
$\text{id}\,:\, \mathcal{X}\to \mathcal{X}$
, takes every element in a set
![]() $\mathcal{X}$
and maps it back to itself.
$\mathcal{X}$
and maps it back to itself.
Notation linked to convergence is defined as follows. For a topological space E we denote its Borel-
![]() $\sigma$
-algebra by
$\sigma$
-algebra by
![]() ${{\mathscr{B}}}(E)$
and the set of bounded continuous functions on E by
${{\mathscr{B}}}(E)$
and the set of bounded continuous functions on E by
![]() $C_b(E)$
. If
$C_b(E)$
. If
![]() $f_n,f$
are real-valued functions on E, we say that
$f_n,f$
are real-valued functions on E, we say that
![]() $f_n$
converges uniformly on compact sets to f if for any compact
$f_n$
converges uniformly on compact sets to f if for any compact
![]() $C \subset E$
the convergence
$C \subset E$
the convergence
![]() $\lim_{n \to \infty} \sup_{x \in C} \lvert f_n(x)-f(x) \rvert = 0$
holds true. Moreover,
$\lim_{n \to \infty} \sup_{x \in C} \lvert f_n(x)-f(x) \rvert = 0$
holds true. Moreover,
![]() $f_n$
is said to converge uniformly on compact sets to infinity if
$f_n$
is said to converge uniformly on compact sets to infinity if
![]() $\inf_{x \in C} f_n(x) \to \infty$
for compact sets
$\inf_{x \in C} f_n(x) \to \infty$
for compact sets
![]() $C \subset E$
as
$C \subset E$
as
![]() $n\to \infty$
. Weak convergence of measures on E is abbreviated by
$n\to \infty$
. Weak convergence of measures on E is abbreviated by
![]() ${{\,\overset {\mathrm {w} }{\longrightarrow }\,}}$
. For random elements
${{\,\overset {\mathrm {w} }{\longrightarrow }\,}}$
. For random elements
![]() $X, X_1,X_2,\ldots$
defined on the same probability space, we say
$X, X_1,X_2,\ldots$
defined on the same probability space, we say
![]() $\{X_n\}$
converges in distribution to X, and we write
$\{X_n\}$
converges in distribution to X, and we write
![]() $X_n{{\,\overset {d }{\longrightarrow }\,}} X$
, if the distributions
$X_n{{\,\overset {d }{\longrightarrow }\,}} X$
, if the distributions
![]() $P_n$
of the
$P_n$
of the
![]() $X_n$
converge weakly to the distribution P of X, that is, if
$X_n$
converge weakly to the distribution P of X, that is, if
![]() $P_n{{\,\overset {\mathrm {w} }{\longrightarrow }\,}} P$
.
$P_n{{\,\overset {\mathrm {w} }{\longrightarrow }\,}} P$
.
2. Theory for hidden tail chains of homogeneous Markov chains
2.1. Overview
In this section we present results for
![]() $\{X_t\,:\, t\in {{\mathbb{Z}}}\}$
being a homogeneous Markov chain, with an extreme value at
$\{X_t\,:\, t\in {{\mathbb{Z}}}\}$
being a homogeneous Markov chain, with an extreme value at
![]() $X_0$
. That is, we assume that we have the distribution function
$X_0$
. That is, we assume that we have the distribution function
![]() $F_0$
for
$F_0$
for
![]() $X_0$
, for
$X_0$
, for
![]() $k>1$
with an initial conditional joint distribution function
$k>1$
with an initial conditional joint distribution function
![]() $F_{1:k-1 \mid 0}({\boldsymbol{x}}_{1\, : \, k-1}\, \mid \, x_0)= \Pr({\boldsymbol{X}}_{1\, : \, k-1}\le {\boldsymbol{x}}_{1\, : \, k-1}\, \mid \, X_0=x_0)$
, for
$F_{1:k-1 \mid 0}({\boldsymbol{x}}_{1\, : \, k-1}\, \mid \, x_0)= \Pr({\boldsymbol{X}}_{1\, : \, k-1}\le {\boldsymbol{x}}_{1\, : \, k-1}\, \mid \, X_0=x_0)$
, for
![]() ${\boldsymbol{x}}_{1\, : \, k-1}\in {{{\mathbb{R}}}}^{k-1}$
, and we have time-invariant forward and backward one-step transition probability kernels
${\boldsymbol{x}}_{1\, : \, k-1}\in {{{\mathbb{R}}}}^{k-1}$
, and we have time-invariant forward and backward one-step transition probability kernels
![]() $\pi$
and
$\pi$
and
![]() $\pi^{-}$
given by
$\pi^{-}$
given by
for
![]() $t\ge k$
and
$t\ge k$
and
![]() $t\ge 1$
, respectively. So in Section 2 we do not impose structure on the marginal distribution of
$t\ge 1$
, respectively. So in Section 2 we do not impose structure on the marginal distribution of
![]() $X_t$
for
$X_t$
for
![]() $t\not= 0$
, or derive how the results relate to the joint distributions of
$t\not= 0$
, or derive how the results relate to the joint distributions of
![]() ${\boldsymbol{X}}_{t-k\, :t}$
for any t; that is considered in Section 3, where stationarity assumptions are made.
${\boldsymbol{X}}_{t-k\, :t}$
for any t; that is considered in Section 3, where stationarity assumptions are made.
Under weak assumptions, in Section 2 we show how the functions
![]() $a_t(x), b_t(x)$
for
$a_t(x), b_t(x)$
for
![]() $t=1,\ldots ,k-1$
and the update functions of (1) and (3), respectively, are connected to transition functionals a and b and the hidden tail chain. From the chosen initial conditional distribution
$t=1,\ldots ,k-1$
and the update functions of (1) and (3), respectively, are connected to transition functionals a and b and the hidden tail chain. From the chosen initial conditional distribution
![]() $F_{1:k-1 \mid 0}$
, we can derive the norming functions
$F_{1:k-1 \mid 0}$
, we can derive the norming functions
![]() $a_t(x)$
and
$a_t(x)$
and
![]() $b_t(x)$
for
$b_t(x)$
for
![]() $t=1, \ldots ,k-1$
. We consider three different scenarios for their asymptotic behaviour. Specifically, in Section 2.3, we have
$t=1, \ldots ,k-1$
. We consider three different scenarios for their asymptotic behaviour. Specifically, in Section 2.3, we have
![]() $a_t(x)/b_t(x)\rightarrow \infty$
as
$a_t(x)/b_t(x)\rightarrow \infty$
as
![]() $x\rightarrow \infty$
. In Section 2.4 we cover the case where
$x\rightarrow \infty$
. In Section 2.4 we cover the case where
![]() $a_t(x) = 0$
for all
$a_t(x) = 0$
for all
![]() $x > 0$
and
$x > 0$
and
![]() $b_t(x)\to \infty$
as
$b_t(x)\to \infty$
as
![]() $x\to \infty$
, but implicitly that section also covers the case
$x\to \infty$
, but implicitly that section also covers the case
![]() $a_t(x)=O(b_t(x))$
as
$a_t(x)=O(b_t(x))$
as
![]() $x\to \infty$
, where in that case the associated
$x\to \infty$
, where in that case the associated
![]() $a_t(x)/b_t(x)$
term in (2) may tend to a constant. In Section 2.5 we consider the cases where both
$a_t(x)/b_t(x)$
term in (2) may tend to a constant. In Section 2.5 we consider the cases where both
![]() $a_t(x)$
and
$a_t(x)$
and
![]() $b_t(x)$
are invariant to x. Sections 2.3–2.5 focus on forward hidden tail chains, whereas in Section 2.6 we look at the joint behaviour of backward and forward hidden tail chains; we therefore drop the term forward in describing
$b_t(x)$
are invariant to x. Sections 2.3–2.5 focus on forward hidden tail chains, whereas in Section 2.6 we look at the joint behaviour of backward and forward hidden tail chains; we therefore drop the term forward in describing
![]() $\pi$
until then.
$\pi$
until then.
2.2. Marginal standardization
To facilitate the generality of our theoretical developments, our assumptions about the margins of the process throughout Section 2 only concern the tail behaviour of the random variable at which we condition the Markov process to exceed a level. This assumption is in the style of theoretical approaches in conditional extreme value theory [Reference Heffernan and Resnick8] and is made precise by Assumption
![]() ${{A}}_0$
.
${{A}}_0$
.
Assumption 1. The distribution
![]() $F_0$
has upper endpoint
$F_0$
has upper endpoint
![]() $\infty$
, and there exist a non-degenerate probability distribution
$\infty$
, and there exist a non-degenerate probability distribution
![]() $H_0$
on
$H_0$
on
![]() $[0,\infty)$
and a measurable norming function
$[0,\infty)$
and a measurable norming function
![]() $\sigma(v)>0$
such that
$\sigma(v)>0$
such that
From [Reference Pickands24], the limit distribution
![]() $H_0$
can be identified by a generalized Pareto distribution with a non-negative shape parameter, i.e.
$H_0$
can be identified by a generalized Pareto distribution with a non-negative shape parameter, i.e.
![]() $H_0(x)=1-(1+\xi x)^{-1/\xi}$
, for
$H_0(x)=1-(1+\xi x)^{-1/\xi}$
, for
![]() $x>0$
and
$x>0$
and
![]() $\xi\ge 0$
. This covers the Pareto distribution, with power-law decay, when
$\xi\ge 0$
. This covers the Pareto distribution, with power-law decay, when
![]() $\xi>0$
, and the exponential distribution when
$\xi>0$
, and the exponential distribution when
![]() $\xi=0$
, taken as the limit as
$\xi=0$
, taken as the limit as
![]() $\xi\rightarrow 0$
.
$\xi\rightarrow 0$
.
2.3. Transitional behaviour for chains with location and scale norming
In this section we consider homogeneous Markov chains where the initial conditional distribution
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that in the limit (1) we have functions
$F_{1\, : \, k-1\, \mid \, 0}$
is such that in the limit (1) we have functions
![]() $a_t(x)/b_t(x)\rightarrow \infty$
as
$a_t(x)/b_t(x)\rightarrow \infty$
as
![]() $x\rightarrow \infty$
for all
$x\rightarrow \infty$
for all
![]() $t=1, \ldots ,k-1$
when
$t=1, \ldots ,k-1$
when
![]() $k>1$
. Specifically, Assumption
$k>1$
. Specifically, Assumption
![]() ${A}_1$
ensures that, given that an extreme event
${A}_1$
ensures that, given that an extreme event
![]() $\{X_0=v\}$
occurs at time
$\{X_0=v\}$
occurs at time
![]() $t=0$
, there exist normalizing functions
$t=0$
, there exist normalizing functions
![]() $a_t(x)$
and
$a_t(x)$
and
![]() $b_t(x)$
for
$b_t(x)$
for
![]() $t=1, \ldots ,k-1$
such that if the arguments of
$t=1, \ldots ,k-1$
such that if the arguments of
![]() $F_{1\, : \, k-1\, \mid \, 0}$
are affine-transformed using these functions, then a non-degenerate limiting initial conditional distribution G is obtained for
$F_{1\, : \, k-1\, \mid \, 0}$
are affine-transformed using these functions, then a non-degenerate limiting initial conditional distribution G is obtained for
![]() $F_{1\, : \, k-1\, \mid \, 0}$
, in the limit as
$F_{1\, : \, k-1\, \mid \, 0}$
, in the limit as
![]() $v\to\infty$
. This provides the first
$v\to\infty$
. This provides the first
![]() $k-1$
renormalized states of the Markov process after
$k-1$
renormalized states of the Markov process after
![]() $X_0$
.
$X_0$
.
Assumption 2. (Behaviour of initial states in the presence of an extreme event). If
![]() $k>1$
, the initial conditional joint distribution function
$k>1$
, the initial conditional joint distribution function
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that there exist the following:
$F_{1\, : \, k-1\, \mid \, 0}$
is such that there exist the following:
-
(i) for
 $t=1,\ldots,k-1$
, measurable functions
$t=1,\ldots,k-1$
, measurable functions
 $a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
$a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
 $b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, satisfying
$b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, satisfying
 $a_t(v)+b_t(v)\,x\to \infty$
as
$a_t(v)+b_t(v)\,x\to \infty$
as
 $v\to \infty$
, for all fixed
$v\to \infty$
, for all fixed
 $x\in {{{\mathbb{R}}}}$
;
$x\in {{{\mathbb{R}}}}$
; -
(ii) a distribution G supported on
 ${{{\mathbb{R}}}}^{k-1}$
that has non-degenerate margins such that
${{{\mathbb{R}}}}^{k-1}$
that has non-degenerate margins such that  \begin{eqnarray*} && {{\mathbb{P}}}\,\bigg(\frac{{\boldsymbol{X}}_{1\,:\,k-1}-{\boldsymbol{a}}_{1\,:\,k-1}(v)}{{\boldsymbol{b}}_{1\,:\,k-1}(v)} \in d {\boldsymbol{z}}_{1\,:\,k-1} \,\Big|\,X_0 = v\bigg) {{\,\overset {\mathrm {w} }{\longrightarrow }\,}} G(d {\boldsymbol{z}}_{1\,:\,k-1})\quad \text{as $v\to \infty$.} \end{eqnarray*}
\begin{eqnarray*} && {{\mathbb{P}}}\,\bigg(\frac{{\boldsymbol{X}}_{1\,:\,k-1}-{\boldsymbol{a}}_{1\,:\,k-1}(v)}{{\boldsymbol{b}}_{1\,:\,k-1}(v)} \in d {\boldsymbol{z}}_{1\,:\,k-1} \,\Big|\,X_0 = v\bigg) {{\,\overset {\mathrm {w} }{\longrightarrow }\,}} G(d {\boldsymbol{z}}_{1\,:\,k-1})\quad \text{as $v\to \infty$.} \end{eqnarray*}
Note that such conditions are not required by [Reference Papastathopoulos, Strokorb, Tawn and Butler20] when
![]() $k=1$
. Assumption 2 implies that
$k=1$
. Assumption 2 implies that
![]() $a_t(v) \to \infty$
and
$a_t(v) \to \infty$
and
![]() $b_t(v)=o(a_t(v))$
as
$b_t(v)=o(a_t(v))$
as
![]() $v\to \infty$
, since if
$v\to \infty$
, since if
![]() $b_t(v)$
grew as fast as, or faster than,
$b_t(v)$
grew as fast as, or faster than,
![]() $a_t(t)$
, then for a suitably selected
$a_t(t)$
, then for a suitably selected
![]() $x\in \mathbb{R}$
, with x negative, we would have that
$x\in \mathbb{R}$
, with x negative, we would have that
![]() $a_t(v)+b_t(v)x \rightarrow -\infty$
as
$a_t(v)+b_t(v)x \rightarrow -\infty$
as
![]() $v \rightarrow \infty$
.
$v \rightarrow \infty$
.
Remark 1. When saying that a distribution is supported on a subset A of
![]() ${{{\mathbb{R}}}}^k$
, we do not allow the distribution to place mass at the boundary
${{{\mathbb{R}}}}^k$
, we do not allow the distribution to place mass at the boundary
![]() $\partial A$
of A. This is an important distinction which restricts the class of possible initial conditional distribution functions
$\partial A$
of A. This is an important distinction which restricts the class of possible initial conditional distribution functions
![]() $F_{1\, : \, k-1\, \mid \, 0}$
that the homogeneous Markov chain can possess. See Example 4 in Section 5.3 for a stationary Markov chain which has limit G with mass on the boundary, and hence breaks the conditions of Assumption 2.
$F_{1\, : \, k-1\, \mid \, 0}$
that the homogeneous Markov chain can possess. See Example 4 in Section 5.3 for a stationary Markov chain which has limit G with mass on the boundary, and hence breaks the conditions of Assumption 2.
After we have initialized the states
![]() $X_0,\ldots, X_{k-1}$
, a complete characterization of the advancing sequence of states for
$X_0,\ldots, X_{k-1}$
, a complete characterization of the advancing sequence of states for
![]() $t\geq k$
is given by the one-step transition probability kernel
$t\geq k$
is given by the one-step transition probability kernel
![]() $\pi({\boldsymbol{x}}_{t-k\,:\,t-1}, x_t)$
. To motivate our next assumption about the behaviour of the transition probability kernel of the process, consider how a complete characterization may be given for higher-order Markov processes with
$\pi({\boldsymbol{x}}_{t-k\,:\,t-1}, x_t)$
. To motivate our next assumption about the behaviour of the transition probability kernel of the process, consider how a complete characterization may be given for higher-order Markov processes with
![]() $k>1$
using induction on
$k>1$
using induction on
![]() ${{\mathbb{N}}}$
. Fix a
${{\mathbb{N}}}$
. Fix a
![]() $t \geq k> 1$
and assume that there exist sequences of norming functions
$t \geq k> 1$
and assume that there exist sequences of norming functions
![]() $a_i$
and
$a_i$
and
![]() $b_i$
,
$b_i$
,
![]() $i=1,\ldots, t-1$
, such that
$i=1,\ldots, t-1$
, such that
where each
![]() ${{Z}}_i$
is a random variable with a non-degenerate distribution on
${{Z}}_i$
is a random variable with a non-degenerate distribution on
![]() ${{{\mathbb{R}}}}$
. Therefore, what is required is to assert that, under the induction hypothesis, we can find
${{{\mathbb{R}}}}$
. Therefore, what is required is to assert that, under the induction hypothesis, we can find
![]() $a_t$
and
$a_t$
and
![]() $b_t$
such that for
$b_t$
such that for
![]() ${\boldsymbol{a}}_{1\,:\,t}=({\boldsymbol{a}}_{1\,:\,t-1}, a_t)$
and
${\boldsymbol{a}}_{1\,:\,t}=({\boldsymbol{a}}_{1\,:\,t-1}, a_t)$
and
![]() ${\boldsymbol{b}}_{1\,:\,t}=({\boldsymbol{b}}_{1\,:\,t-1}, b_t)$
, we have that
${\boldsymbol{b}}_{1\,:\,t}=({\boldsymbol{b}}_{1\,:\,t-1}, b_t)$
, we have that
![]() $\{{\boldsymbol{X}}_{1\,:\,t} - {\boldsymbol{a}}_{1\,:\,t}( X_0)\}/{\boldsymbol{b}}_{1\,:\,t}(X_0) \mid \{X_0>u\} {{\,\overset {d }{\longrightarrow }\,}} {\boldsymbol{Z}}_{1\,:\,t}$
, as
$\{{\boldsymbol{X}}_{1\,:\,t} - {\boldsymbol{a}}_{1\,:\,t}( X_0)\}/{\boldsymbol{b}}_{1\,:\,t}(X_0) \mid \{X_0>u\} {{\,\overset {d }{\longrightarrow }\,}} {\boldsymbol{Z}}_{1\,:\,t}$
, as
![]() $u\to\infty$
, where
$u\to\infty$
, where
![]() ${{Z}}_t$
is a random variable with a non-degenerate distribution supported on
${{Z}}_t$
is a random variable with a non-degenerate distribution supported on
![]() ${{{\mathbb{R}}}}$
. To motivate our assumptions that guarantee this latter convergence, it suffices to consider marginal convergence, that is, the case where the distribution of
${{{\mathbb{R}}}}$
. To motivate our assumptions that guarantee this latter convergence, it suffices to consider marginal convergence, that is, the case where the distribution of
![]() $\{X_t-a_t(X_0)\}/b_t(X_0)\mid \{X_0 > u\}$
converges weakly under the induction hypothesis. Standard calculations give that
$\{X_t-a_t(X_0)\}/b_t(X_0)\mid \{X_0 > u\}$
converges weakly under the induction hypothesis. Standard calculations give that

for
![]() $t \geq k$
. This expression can be simplified by exploiting the Markov chain properties of
$t \geq k$
. This expression can be simplified by exploiting the Markov chain properties of
![]() $\{X_t\}$
and by rearranging the expression to clarify the connections with transitions from the initial
$\{X_t\}$
and by rearranging the expression to clarify the connections with transitions from the initial
![]() $k-1$
states after an extreme event by a change of the variables being integrated. First, replace
$k-1$
states after an extreme event by a change of the variables being integrated. First, replace
![]() $a_t(X_0)$
by
$a_t(X_0)$
by
![]() $a_t(x_0)$
in the innermost integral, by virtue of the conditioning on the exact value of
$a_t(x_0)$
in the innermost integral, by virtue of the conditioning on the exact value of
![]() $X_0$
being equal to
$X_0$
being equal to
![]() $x_0$
. Second, use the Markov property so that the conditioning on all previous states is reduced to conditioning on the previous k states. Third, change variables to
$x_0$
. Second, use the Markov property so that the conditioning on all previous states is reduced to conditioning on the previous k states. Third, change variables to
![]() $z_0 = \{x_0 - u\}/\sigma(u)$
and
$z_0 = \{x_0 - u\}/\sigma(u)$
and
![]() $z_i = \{x_i - a_i(x_0)\}/b_i(x_0)$
, for
$z_i = \{x_i - a_i(x_0)\}/b_i(x_0)$
, for
![]() $i=1,\ldots,t-1$
. This sequence of operations shows that (5) equals
$i=1,\ldots,t-1$
. This sequence of operations shows that (5) equals

for
![]() $t\geq k$
, where
$t\geq k$
, where
![]() $a_0(x)=x$
,
$a_0(x)=x$
,
![]() $b_0(x)=1$
for all
$b_0(x)=1$
for all
![]() $x\in {{{\mathbb{R}}}}$
, and
$x\in {{{\mathbb{R}}}}$
, and
![]() $v_u(z_0)=u + \sigma(u)\, z_0$
. Hence, convergence of the innermost integral in the curly parentheses in (6) is necessary for marginal convergence of the probability (5) as
$v_u(z_0)=u + \sigma(u)\, z_0$
. Hence, convergence of the innermost integral in the curly parentheses in (6) is necessary for marginal convergence of the probability (5) as
![]() $v\rightarrow \infty$
. To further simplify this integral, for
$v\rightarrow \infty$
. To further simplify this integral, for
![]() ${\boldsymbol{z}}\in {{{\mathbb{R}}}}^{k-1}$
, let
${\boldsymbol{z}}\in {{{\mathbb{R}}}}^{k-1}$
, let
Then, observe that for functions
![]() $a\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}$
and
$a\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}$
and
![]() $b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
, which for the present are arbitrary functions but are made precise in Proposition 1, the innermost integral can be written as
$b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
, which for the present are arbitrary functions but are made precise in Proposition 1, the innermost integral can be written as

where
![]() $\psi_{t,u}^a$
and
$\psi_{t,u}^a$
and
![]() $\psi_{t,u}^b$
are given in the expression (8) and depend on the functions a, b and the normings
$\psi_{t,u}^b$
are given in the expression (8) and depend on the functions a, b and the normings
![]() $a_t, b_t$
,
$a_t, b_t$
,
![]() $t \geq k$
. Writing the integral in this way provides the connection between the convergence of the transition probability kernel
$t \geq k$
. Writing the integral in this way provides the connection between the convergence of the transition probability kernel
![]() $\pi$
, defined in the expression (4), and the required marginal convergence.
$\pi$
, defined in the expression (4), and the required marginal convergence.
These observations motivate our next assumption, which serves as an extension to higher order
![]() $(k>1)$
of the conditions established by [Reference Papastathopoulos, Strokorb, Tawn and Butler20] in the context of first-order Markov chains. Specifically, to establish the convergence of this rearranged integral, the oscillation of the functions a and b in a neighbourhood of infinity needs to be controlled, i.e. a and b need to be chosen so that the functions
$(k>1)$
of the conditions established by [Reference Papastathopoulos, Strokorb, Tawn and Butler20] in the context of first-order Markov chains. Specifically, to establish the convergence of this rearranged integral, the oscillation of the functions a and b in a neighbourhood of infinity needs to be controlled, i.e. a and b need to be chosen so that the functions
![]() $\psi_{t,u}^a$
and
$\psi_{t,u}^a$
and
![]() $\psi_{t,u}^b$
converge locally uniformly to real-valued limits (
$\psi_{t,u}^b$
converge locally uniformly to real-valued limits (
![]() $\psi_t^a$
and
$\psi_t^a$
and
![]() $\psi_t^b$
, respectively), as
$\psi_t^b$
, respectively), as
![]() $u\to\infty$
. These conditions are made precise by Assumption 3.
$u\to\infty$
. These conditions are made precise by Assumption 3.
Assumption 3. (Behaviour of the next state of the process as the previous states become extreme.) Let
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $a_0(x)=x$
, and
$a_0(x)=x$
, and
![]() $b_0(x)=1$
. If
$b_0(x)=1$
. If
![]() $k > 1$
, suppose that for
$k > 1$
, suppose that for
![]() ${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 2 holds with norming functions
${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 2 holds with norming functions
![]() ${\boldsymbol{a}}_{1\,:\,k-1}$
and
${\boldsymbol{a}}_{1\,:\,k-1}$
and
![]() ${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
![]() $\pi$
is such that there exist the following:
$\pi$
is such that there exist the following:
-
(i) for
 $t=k,k+1,\ldots$
, measurable functions
$t=k,k+1,\ldots$
, measurable functions
 $a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
$a_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
 $b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, continuous update functions
$b_t\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, continuous update functions
 $\psi_{t}^a\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
$\psi_{t}^a\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
 $\psi_t^b\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, and measurable functions
$\psi_t^b\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, and measurable functions
 $a\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
$a\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
 $b\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, such that for all
$b\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, such that for all
 ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
(8)whenever
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
(8)whenever \begin{equation} \psi_{t,v}^a({\boldsymbol{z}}_v)\,:\!=\,\frac{a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))-a_{t}(v)}{b_{t}(v)} \to \psi_{t}^a( {\boldsymbol{z}}) \quad \text{and} \quad \psi_{t,v}^b({\boldsymbol{z}}_v)\,:\!=\,\frac{b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))}{b_{t}(v)}\to \psi_{t}^b({\boldsymbol{z}}) \end{equation}
\begin{equation} \psi_{t,v}^a({\boldsymbol{z}}_v)\,:\!=\,\frac{a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))-a_{t}(v)}{b_{t}(v)} \to \psi_{t}^a( {\boldsymbol{z}}) \quad \text{and} \quad \psi_{t,v}^b({\boldsymbol{z}}_v)\,:\!=\,\frac{b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))}{b_{t}(v)}\to \psi_{t}^b({\boldsymbol{z}}) \end{equation}
 ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
 $v\to\infty$
, where
$v\to\infty$
, where
 ${\boldsymbol{A}}_{t}(v,{\boldsymbol{z}})$
is defined by (7);
${\boldsymbol{A}}_{t}(v,{\boldsymbol{z}})$
is defined by (7);
-
(ii) a non-degenerate distribution
 $K_A$
supported on
$K_A$
supported on
 ${{{\mathbb{R}}}}$
, such that for all
${{{\mathbb{R}}}}$
, such that for all
 ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
and for any
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
and for any
 $f\in C_b({{{\mathbb{R}}}})$
(9)whenever
$f\in C_b({{{\mathbb{R}}}})$
(9)whenever \begin{equation} \int_{{{\mathbb{R}}}} f(x) \pi[{\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v), a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v)) + b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))\,dx]\to\int_{{{{\mathbb{R}}}}}f(x) K_A(dx),\quad t=k,k+1,\ldots, \end{equation}
\begin{equation} \int_{{{\mathbb{R}}}} f(x) \pi[{\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v), a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v)) + b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))\,dx]\to\int_{{{{\mathbb{R}}}}}f(x) K_A(dx),\quad t=k,k+1,\ldots, \end{equation}
 ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
 $v\to \infty$
.
$v\to \infty$
.
We are now able to characterize the hidden tail chain for this type of homogeneous Markov chain. Specifically, we combine assumptions about the marginal tail behaviour of
![]() $X_0$
(through
$X_0$
(through
![]() $H_0$
), the conditional limiting behaviour of the initial state vector given that
$H_0$
), the conditional limiting behaviour of the initial state vector given that
![]() $X_0$
is extreme (described by G), and the constraints on the chain’s transitional behaviour, represented by the functions a and b, through
$X_0$
is extreme (described by G), and the constraints on the chain’s transitional behaviour, represented by the functions a and b, through
![]() $\pi$
. This is asserted by Theorem 1.
$\pi$
. This is asserted by Theorem 1.
Theorem 1. Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1, 2, and 3. Then as
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1, 2, and 3. Then as
![]() $v\to \infty$
$v\to \infty$
where
-
(i)
 $E_0\sim H_0$
and the vector
$E_0\sim H_0$
and the vector
 $({{Z}}_1,{{Z}}_2,\ldots,{{Z}}_t) $
are independent, for all
$({{Z}}_1,{{Z}}_2,\ldots,{{Z}}_t) $
are independent, for all
 $t\ge 1$
,
$t\ge 1$
, -
(ii)
 ${{Z}}_0=0$
almost surely (a.s.),
${{Z}}_0=0$
almost surely (a.s.),
 $({{Z}}_1,\ldots,{{Z}}_{k-1})\sim G$
, and (11)for a sequence of i.i.d. random variables
$({{Z}}_1,\ldots,{{Z}}_{k-1})\sim G$
, and (11)for a sequence of i.i.d. random variables \begin{equation} {{Z}}_{t} = \psi_t^a( {\boldsymbol{Z}}_{t-k\,:\,t-1}) + \psi_t^b( {\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\qquad t=k,k+1,\ldots, \end{equation}
\begin{equation} {{Z}}_{t} = \psi_t^a( {\boldsymbol{Z}}_{t-k\,:\,t-1}) + \psi_t^b( {\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\qquad t=k,k+1,\ldots, \end{equation}
 $\varepsilon_k, \varepsilon_{k+1}, \ldots $
with non-degenerate marginal distribution function
$\varepsilon_k, \varepsilon_{k+1}, \ldots $
with non-degenerate marginal distribution function
 $K_A$
, defined by the limit (9).
$K_A$
, defined by the limit (9).
Theorem 1 provides a highly structured limiting hidden tail chain, with the first value distributed as a generalized Pareto variable, with non-negative shape parameter, which is independent of the rest of the hidden tail; an initial conditional distribution given by G; and subsequently a kth-order autoregressive behaviour. In Theorem 1, we do not attempt to clarify what properties
![]() $\psi_t^a$
and
$\psi_t^a$
and
![]() $\psi_t^b$
possess, or to give how the transition functionals a and b are derived. Additional assumptions in later sections provide these details. However, under the current assumptions, Proposition 1 makes a connection between the required
$\psi_t^b$
possess, or to give how the transition functionals a and b are derived. Additional assumptions in later sections provide these details. However, under the current assumptions, Proposition 1 makes a connection between the required
![]() $a_t$
and
$a_t$
and
![]() $b_t$
functions for
$b_t$
functions for
![]() $t\ge k$
with these functions for
$t\ge k$
with these functions for
![]() $1\le t\le k-1$
.
$1\le t\le k-1$
.
Proposition 1. Let
![]() $a\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}$
and
$a\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}$
and
![]() $b\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}_+$
be measurable maps. Let
$b\,:\,{{{\mathbb{R}}}}^k\to {{{\mathbb{R}}}}_+$
be measurable maps. Let
![]() $t\geq k$
and
$t\geq k$
and
![]() ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
. The following statements are equivalent:
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
. The following statements are equivalent:
-
(i) There exist measurable functions
 $a_t\,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}$
,
$a_t\,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}$
,
 $b_t\,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}_+$
and continuous functions
$b_t\,:\,{{{\mathbb{R}}}}\to {{{\mathbb{R}}}}_+$
and continuous functions
 $\psi_t^a\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}$
and
$\psi_t^a\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}$
and
 $\psi_t^b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
such that the convergence (8) holds.
$\psi_t^b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
such that the convergence (8) holds. -
(ii) There exist continuous functions
 $\lambda_t^a\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}$
and
$\lambda_t^a\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}$
and
 $\lambda_t^b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
such that for all
$\lambda_t^b\,:\,{{{\mathbb{R}}}}^k\to{{{\mathbb{R}}}}_+$
such that for all
 ${\boldsymbol{z}} \in {{{\mathbb{R}}}}^k$
whenever
${\boldsymbol{z}} \in {{{\mathbb{R}}}}^k$
whenever \begin{eqnarray*} && \frac{a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))-a({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}{b({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}\to\lambda_{t}^a( {\boldsymbol{z}}) \quad\text{and} \quad \frac{b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))}{b({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}\to \lambda_t^b({\boldsymbol{z}})\end{eqnarray*}
\begin{eqnarray*} && \frac{a({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))-a({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}{b({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}\to\lambda_{t}^a( {\boldsymbol{z}}) \quad\text{and} \quad \frac{b({\boldsymbol{A}}_{t}(v,{\boldsymbol{z}}_v))}{b({\boldsymbol{A}}_{t}(v,{\textbf{0}}_k))}\to \lambda_t^b({\boldsymbol{z}})\end{eqnarray*}
 ${\boldsymbol{z}}_v\to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v\to {\boldsymbol{z}}$
as
 $v\to \infty$
, where a and b are as defined in Assumption 3 and
$v\to \infty$
, where a and b are as defined in Assumption 3 and
 ${\boldsymbol{A}}_{t}(v,{\boldsymbol{z}})$
is as defined by (7).
${\boldsymbol{A}}_{t}(v,{\boldsymbol{z}})$
is as defined by (7).
2.4. Transitional behaviour for nonnegative chains with only scale norming
Consider nonnegative homogeneous Markov chains, i.e. with
![]() $F_t(0)=0$
for all
$F_t(0)=0$
for all
![]() $t\in {{\mathbb{Z}}}$
, where the initial conditional distribution
$t\in {{\mathbb{Z}}}$
, where the initial conditional distribution
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that in the limit (1) we have functions such that there is no need for norming of the location, i.e. we can take
$F_{1\, : \, k-1\, \mid \, 0}$
is such that in the limit (1) we have functions such that there is no need for norming of the location, i.e. we can take
![]() $a_t(X_0)=0$
, and yet we need a scaling as
$a_t(X_0)=0$
, and yet we need a scaling as
![]() $b_t(x)\rightarrow \infty$
for
$b_t(x)\rightarrow \infty$
for
![]() $t=1, \ldots , k-1$
, when
$t=1, \ldots , k-1$
, when
![]() $k>1$
. As in [Reference Papastathopoulos, Strokorb, Tawn and Butler20], we require extra care relative to Section 2.3 since the convergences in Assumption 3(i) will be satisfied for all
$k>1$
. As in [Reference Papastathopoulos, Strokorb, Tawn and Butler20], we require extra care relative to Section 2.3 since the convergences in Assumption 3(i) will be satisfied for all
![]() $x \in (0, \infty)$
, but not all
$x \in (0, \infty)$
, but not all
![]() $x \in [0, \infty)$
. Hence, we have to control the mass of the limiting renormalized initial conditional distribution and the limiting renormalized transition probability kernel of the Markov process. The strategy in this case is otherwise similar to that of Section 2.3, so we give only the statements of the key equivalent results.
$x \in [0, \infty)$
. Hence, we have to control the mass of the limiting renormalized initial conditional distribution and the limiting renormalized transition probability kernel of the Markov process. The strategy in this case is otherwise similar to that of Section 2.3, so we give only the statements of the key equivalent results.
Assumption 4. (Behaviour of initial states in the presence of an extreme event.) If
![]() $k>1$
, the initial conditional joint distribution function
$k>1$
, the initial conditional joint distribution function
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that there exist measurable functions
$F_{1\, : \, k-1\, \mid \, 0}$
is such that there exist measurable functions
![]() $b_t\,:\,{{{\mathbb{R}}}}_+\to{{{\mathbb{R}}}}_+$
for
$b_t\,:\,{{{\mathbb{R}}}}_+\to{{{\mathbb{R}}}}_+$
for
![]() $t=1,\ldots,k-1$
such that
$t=1,\ldots,k-1$
such that
![]() $b_t(v)\to \infty$
as
$b_t(v)\to \infty$
as
![]() $v\to\infty$
, and a non-degenerate distribution function G on
$v\to\infty$
, and a non-degenerate distribution function G on
![]() $[0,\infty)^{k}$
, with no mass at any of the half-planes
$[0,\infty)^{k}$
, with no mass at any of the half-planes
![]() $C_j=\{({{z}}_1,\ldots,{{z}}_{k-1})\in [0,\infty)^{k-1}: {{{z}}_{j} = 0}\}$
, i.e.
$C_j=\{({{z}}_1,\ldots,{{z}}_{k-1})\in [0,\infty)^{k-1}: {{{z}}_{j} = 0}\}$
, i.e.
![]() $G(\{C_j\})=0$
for
$G(\{C_j\})=0$
for
![]() $j=1,\ldots, k-1$
, such that
$j=1,\ldots, k-1$
, such that
Assumption 5. (Behaviour of the next state of the process as the previous states become extreme.) Let
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $b_0(x)=x$
, and when
$b_0(x)=x$
, and when
![]() $k > 1$
, additionally suppose that for
$k > 1$
, additionally suppose that for
![]() ${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 4 holds with norming functions
${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 4 holds with norming functions
![]() ${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
![]() $\pi$
is such that there exist the following:
$\pi$
is such that there exist the following:
-
(i) for
 $t=k,k+1,\ldots$
, measurable functions
$t=k,k+1,\ldots$
, measurable functions
 $b_t\,:\,{{{\mathbb{R}}}}_+ \to {{{\mathbb{R}}}}_+$
, continuous update functions
$b_t\,:\,{{{\mathbb{R}}}}_+ \to {{{\mathbb{R}}}}_+$
, continuous update functions
 $\psi_t^b\,:\,{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
, and a measurable function
$\psi_t^b\,:\,{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
, and a measurable function
 $b\,:\,{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
such that for all
$b\,:\,{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
such that for all
 $\delta_1,\ldots,\delta_k > 0$
and
$\delta_1,\ldots,\delta_k > 0$
and
 ${\boldsymbol{z}} \in [\delta_1,\infty) \times\ldots \times [\delta_k, \infty)$
, (12)whenever
${\boldsymbol{z}} \in [\delta_1,\infty) \times\ldots \times [\delta_k, \infty)$
, (12)whenever \begin{equation} \lim_{v\to\infty} \frac{b( {\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v))}{b_{t}(v)}{=} \psi_{t}^b({\boldsymbol{z}})>0, \end{equation}
\begin{equation} \lim_{v\to\infty} \frac{b( {\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v))}{b_{t}(v)}{=} \psi_{t}^b({\boldsymbol{z}})>0, \end{equation}
 ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
 $v\to \infty$
and
$v\to \infty$
and
 $\sup\{\lVert {\boldsymbol{z}} \lVert_{\infty}\,:\, {\boldsymbol{z}}\in A_c\} \to 0$
as
$\sup\{\lVert {\boldsymbol{z}} \lVert_{\infty}\,:\, {\boldsymbol{z}}\in A_c\} \to 0$
as
 $c\downarrow 0$
, where
$c\downarrow 0$
, where
 ${\boldsymbol{B}}_{t}(v,{\boldsymbol{z}})\,:\!=\, {\boldsymbol{b}}_{t-k\,:\,t-1} (v)\,{\boldsymbol{z}}$
and
${\boldsymbol{B}}_{t}(v,{\boldsymbol{z}})\,:\!=\, {\boldsymbol{b}}_{t-k\,:\,t-1} (v)\,{\boldsymbol{z}}$
and
 $A_c = \big\{{\boldsymbol{z}}\in (0, \infty)^k\,:\, \psi_t^b({\boldsymbol{z}})\leq c\big\}$
, with the convention that
$A_c = \big\{{\boldsymbol{z}}\in (0, \infty)^k\,:\, \psi_t^b({\boldsymbol{z}})\leq c\big\}$
, with the convention that
 $\sup(\emptyset) = 0$
;
$\sup(\emptyset) = 0$
;
-
(ii) a non-degenerate distribution
 $K_B$
supported on
$K_B$
supported on
 $[0,\infty)$
with no mass at
$[0,\infty)$
with no mass at
 $\{0\}$
, that is,
$\{0\}$
, that is,
 $K_B\{0\}=0$
, such that, for any
$K_B\{0\}=0$
, such that, for any
 $f\in C_b({{{\mathbb{R}}}}_+)$
,(13)
$f\in C_b({{{\mathbb{R}}}}_+)$
,(13) \begin{equation} \int_{{{{\mathbb{R}}}}_+}f(x)\, \pi[{\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v),b({\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v))\,dx]\to \int_{{{{\mathbb{R}}}}_+} f(x)\, K_B(dx), \qquad\text{$t=k,k+1,\ldots$,} \end{equation}
\begin{equation} \int_{{{{\mathbb{R}}}}_+}f(x)\, \pi[{\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v),b({\boldsymbol{B}}_{t}(v,{\boldsymbol{z}}_v))\,dx]\to \int_{{{{\mathbb{R}}}}_+} f(x)\, K_B(dx), \qquad\text{$t=k,k+1,\ldots$,} \end{equation}
whenever
![]() ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
![]() $v\to \infty$
.
$v\to \infty$
.
Theorem 2. Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous Markov chain satisfying Assumptions 1, 4, and 5. Then as
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous Markov chain satisfying Assumptions 1, 4, and 5. Then as
![]() $v\to \infty$
$v\to \infty$
where
-
(i)
 $E_0\sim H_0$
and the vector
$E_0\sim H_0$
and the vector
 $({{Z}}_1,{{Z}}_2\ldots,{{Z}}_t) $
are independent for any
$({{Z}}_1,{{Z}}_2\ldots,{{Z}}_t) $
are independent for any
 $t\ge 1$
,
$t\ge 1$
, -
(ii)
 ${{Z}}_0=1$
a.s.,
${{Z}}_0=1$
a.s.,
 $({{Z}}_1,\ldots,{{{Z}}_{k-1}})\sim G$
, and (15)for a sequence of i.i.d. random variables
$({{Z}}_1,\ldots,{{{Z}}_{k-1}})\sim G$
, and (15)for a sequence of i.i.d. random variables \begin{equation} {{Z}}_{t} = \psi_t^b({\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\quad t=k,k+1,\ldots, \end{equation}
\begin{equation} {{Z}}_{t} = \psi_t^b({\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\quad t=k,k+1,\ldots, \end{equation}
 $\varepsilon_k, \varepsilon_{k+1}, \ldots $
with non-degenerate marginal distribution function
$\varepsilon_k, \varepsilon_{k+1}, \ldots $
with non-degenerate marginal distribution function
 $K_B$
defined by the limit (13).
$K_B$
defined by the limit (13).
Remark 2. Theorem 2 appears simply to be the kth-order extension of Theorem 3.1 in [Reference Kulik and Soulier14], but it differs:
![]() $H_0$
includes both Pareto and exponential tails, so it is in a more general class than the Pareto family considered by [Reference Kulik and Soulier14].
$H_0$
includes both Pareto and exponential tails, so it is in a more general class than the Pareto family considered by [Reference Kulik and Soulier14].
2.5. Transitional behaviour for near extremally independent chains
In this section, we consider homogeneous Markov chains where the initial conditional distribution
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that there no norming of the location and no norming of the scale are needed for the limit (1) to hold. This case resembles the formulation of Theorem 1, but has
$F_{1\, : \, k-1\, \mid \, 0}$
is such that there no norming of the location and no norming of the scale are needed for the limit (1) to hold. This case resembles the formulation of Theorem 1, but has
![]() $a_t(v)=0$
and
$a_t(v)=0$
and
![]() $b_t(v)=1$
for all
$b_t(v)=1$
for all
![]() $t\geq 1$
. The next assumption ensures that after an extreme event at time
$t\geq 1$
. The next assumption ensures that after an extreme event at time
![]() $t=0$
, a non-degenerate distribution, given by
$t=0$
, a non-degenerate distribution, given by
![]() $\{X_0=v\}$
, is obtained in the limit as
$\{X_0=v\}$
, is obtained in the limit as
![]() $v\to\infty$
for the first k states of the Markov process, without any renormalization.
$v\to\infty$
for the first k states of the Markov process, without any renormalization.
Assumption 6. (Behaviour of next states in the presence of an extreme event.) If
![]() $k>1$
, the initial conditional joint distribution function
$k>1$
, the initial conditional joint distribution function
![]() $F_{1\, : \, k-1\, \mid \, 0}$
is such that there exists a distribution G supported on
$F_{1\, : \, k-1\, \mid \, 0}$
is such that there exists a distribution G supported on
![]() ${{{\mathbb{R}}}}^{k}$
that has non-degenerate margins such that
${{{\mathbb{R}}}}^{k}$
that has non-degenerate margins such that
[Reference Heffernan and Tawn9] showed that Assumption 6 holds for the Morgenstern copula, with exponential marginals, for
![]() $k\geq 1$
. A related assumption also appears [Reference Maulik, Resnick and Rootzén18] for the case
$k\geq 1$
. A related assumption also appears [Reference Maulik, Resnick and Rootzén18] for the case
![]() $k=1$
with
$k=1$
with
![]() $(X_0, X_1)$
being nonnegative random variables. Here, we note that if
$(X_0, X_1)$
being nonnegative random variables. Here, we note that if
![]() ${\boldsymbol{X}}_{0\,:\,k}$
has the independence copula, then
${\boldsymbol{X}}_{0\,:\,k}$
has the independence copula, then
![]() $G({\boldsymbol{z}}_{1\,:\,k}) = \prod_{j=1}^kF_j(z_j)$
, whereas cases with
$G({\boldsymbol{z}}_{1\,:\,k}) = \prod_{j=1}^kF_j(z_j)$
, whereas cases with
![]() $G_j(z) \geq F_j(z)$
(
$G_j(z) \geq F_j(z)$
(
![]() $G_j(z) \leq F_j(z)$
) for all
$G_j(z) \leq F_j(z)$
) for all
![]() $z\in{{{\mathbb{R}}}}$
, with
$z\in{{{\mathbb{R}}}}$
, with
![]() $G_j$
being the jth marginal distribution of G, correspond to positive (negative) near extremal independence at lag j in the hidden tail chain.
$G_j$
being the jth marginal distribution of G, correspond to positive (negative) near extremal independence at lag j in the hidden tail chain.
Assumptions 1 and 6 are sufficient to establish the weak convergence of the conditioned Markov chain to a hidden tail chain in Theorem 3 below. The proof of this theorem follows along the lines of the proof of Theorem 1 and is omitted for brevity.
Theorem 3. Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1 and 6. Then as
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1 and 6. Then as
![]() $v\to \infty$
$v\to \infty$
where
-
(i)
 $E_0\sim H_0$
and the vector
$E_0\sim H_0$
and the vector
 $({{Z}}_1,{{Z}}_2\ldots,{{Z}}_t) $
are independent for any
$({{Z}}_1,{{Z}}_2\ldots,{{Z}}_t) $
are independent for any
 $t\ge 1$
,
$t\ge 1$
, -
(ii)
 $({{Z}}_1,\ldots,{{Z}}_{k})\sim G$
and where
$({{Z}}_1,\ldots,{{Z}}_{k})\sim G$
and where \begin{align*} {{Z}}_{t}=\pi^{-1}({\boldsymbol{Z}}_{t-k\,:\,t-1}, U_t), \qquad t=k+1,k+2,\ldots, \end{align*}
\begin{align*} {{Z}}_{t}=\pi^{-1}({\boldsymbol{Z}}_{t-k\,:\,t-1}, U_t), \qquad t=k+1,k+2,\ldots, \end{align*}
 $\{U_t\}$
is a sequence of i.i.d. uniform(0,1) random variables for
$\{U_t\}$
is a sequence of i.i.d. uniform(0,1) random variables for
 $t\ge k+1$
,
$t\ge k+1$
,
 $\pi$
is the one-step transition probability kernel for the original Markov chain, and
$\pi$
is the one-step transition probability kernel for the original Markov chain, and
 $\pi^{-1}\,:\,{{{\mathbb{R}}}}^k \times (0,1)\to {{{\mathbb{R}}}}$
with
$\pi^{-1}\,:\,{{{\mathbb{R}}}}^k \times (0,1)\to {{{\mathbb{R}}}}$
with
 $\pi^{-1}({\boldsymbol{z}}, u) \,:\!=\, \inf\{x \in {{{\mathbb{R}}}}\,:\,\pi({\boldsymbol{z}}, x)> u\}$
.
$\pi^{-1}({\boldsymbol{z}}, u) \,:\!=\, \inf\{x \in {{{\mathbb{R}}}}\,:\,\pi({\boldsymbol{z}}, x)> u\}$
.
We note that if
![]() ${\boldsymbol{X}}_{0\,:\,k}$
has the independence copula, then
${\boldsymbol{X}}_{0\,:\,k}$
has the independence copula, then
![]() $\pi^{-1}({\boldsymbol{z}}, u)$
is independent of
$\pi^{-1}({\boldsymbol{z}}, u)$
is independent of
![]() ${\boldsymbol{z}}$
.
${\boldsymbol{z}}$
.
2.6. Back-and-forth hidden tail chains
In the discussion above, formally the entities we have referred to as tail chains and hidden tail chains are in fact forward tail and hidden tail chains [cf. 14]. These describe the behaviour of the Markov chain only forward in time from a large observation. There is also the parallel interest in backward tail and hidden tail chains, to give how the chain evolves into an extreme event, and the joint behaviour of the two, known as back-and-forth tail processes.
Here we focus on an extension of the back-and-forth tail chains developed by [Reference Janßen and Segers11]. The properties of the backward hidden tail chain are similar in structure to those of the forward hidden tail chain identified in Sections 2.3–2.4. To save repetition, here we outline the back-and-forth hidden tail chains for the assumptions in Section 2.3 only. For this purpose, it suffices to consider a straightforward extension of Assumption 3 which allows us to characterize the backward behaviour of the chain from an extreme event by requiring a functional normalization for the backward chain
![]() $X_{-s}\mid {\boldsymbol{X}}_{-(s-1)\,:\,-(s-k)}$
,
$X_{-s}\mid {\boldsymbol{X}}_{-(s-1)\,:\,-(s-k)}$
,
![]() $s\in{{\mathbb{N}}}$
. Clearly, if the chain is time-reversible, then Assumption 3 holds backwards with the same functional normalizations a and b and the same limit distribution
$s\in{{\mathbb{N}}}$
. Clearly, if the chain is time-reversible, then Assumption 3 holds backwards with the same functional normalizations a and b and the same limit distribution
![]() $K_A$
. In general, however, there is no mathematical connection between these forward and backward quantities; Assumption 7 below considers this more general case.
$K_A$
. In general, however, there is no mathematical connection between these forward and backward quantities; Assumption 7 below considers this more general case.
Assumption 7. (Behaviour of the backward state of the process.) Let
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $a_0(x)=x$
, and
$a_0(x)=x$
, and
![]() $b_0(x)=1$
. If
$b_0(x)=1$
. If
![]() $k > 1$
, suppose that for
$k > 1$
, suppose that for
![]() ${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 2 holds with norming functions
${\boldsymbol{X}}_{1\,:\,k-1}$
, Assumption 2 holds with norming functions
![]() ${\boldsymbol{a}}_{1\,:\,k-1}$
and
${\boldsymbol{a}}_{1\,:\,k-1}$
and
![]() ${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
${\boldsymbol{b}}_{1\,:\,k-1}$
. Then assume that
![]() $\pi^-$
is such that there exist the following:
$\pi^-$
is such that there exist the following:
(i) for
![]() $s=1,2,\ldots$
, measurable functions
$s=1,2,\ldots$
, measurable functions
![]() $a_{-s}\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
$a_{-s}\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}$
and
![]() $b_{-s}\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, continuous update functions
$b_{-s}\,:\,{{{\mathbb{R}}}} \to {{{\mathbb{R}}}}_+$
, continuous update functions
![]() $\psi_{-s}^{a^-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
$\psi_{-s}^{a^-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
![]() $\psi_{-s}^{b^-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, and measurable functions
$\psi_{-s}^{b^-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
, and measurable functions
![]() $a^{-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
$a^{-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}$
,
![]() $b^{-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
such that, for all
$b^{-}\,:\,{{{\mathbb{R}}}}^k \to {{{\mathbb{R}}}}_+$
such that, for all
![]() ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
,
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
,
whenever
![]() ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
![]() $v\to\infty$
, where
$v\to\infty$
, where
![]() ${\boldsymbol{A}}_{-s}(v,{\boldsymbol{z}})\,:\!=\, {\boldsymbol{a}}_{-s+1\,:\,-s+k}(v)+{\boldsymbol{b}}_{-s+1\,:\,-s+k} (v)\,{\boldsymbol{z}}$
;
${\boldsymbol{A}}_{-s}(v,{\boldsymbol{z}})\,:\!=\, {\boldsymbol{a}}_{-s+1\,:\,-s+k}(v)+{\boldsymbol{b}}_{-s+1\,:\,-s+k} (v)\,{\boldsymbol{z}}$
;
(ii) a non-degenerate distribution
![]() $K_A^{-}$
supported on
$K_A^{-}$
supported on
![]() ${{{\mathbb{R}}}}$
, such that for all
${{{\mathbb{R}}}}$
, such that for all
![]() ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
and for any
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
and for any
![]() $f\in C_b({{{\mathbb{R}}}})$
,
$f\in C_b({{{\mathbb{R}}}})$
,
![]() $s=1,2,\ldots$
, whenever
$s=1,2,\ldots$
, whenever
![]() ${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
${\boldsymbol{z}}_v \to {\boldsymbol{z}}$
as
![]() $v\to \infty$
.
$v\to \infty$
.
The back-and-forth hidden tail chain is presented in Theorem 4. For the sake of brevity, we do not include its proof, as this is identical to the proof of Theorem 1.
Theorem 4. Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1, 2, 3, and 7. Then as
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a homogeneous kth-order Markov chain satisfying Assumptions 1, 2, 3, and 7. Then as
![]() $v\to \infty$
$v\to \infty$
 \begin{align*} &\bigg(\frac{{\boldsymbol{X}}_{-s\,:\,-1} - {\boldsymbol{a}}_{-s\,:\,-1}(X_0)}{{\boldsymbol{b}}_{-s\,:\,-1}(X_0)},\frac{X_0 - v}{\sigma(v)},\frac{{\boldsymbol{X}}_{1\,:\,t} - {\boldsymbol{a}}_{1\,:\,t}(X_0)}{{\boldsymbol{b}}_{1\,:\,t}(X_0)}\bigg)\,\Big|\,\{X_0>v\} \\\\& {{\,\overset {d }{\longrightarrow }\,}} ({\boldsymbol{Z}}_{-s\,:\,-1},E_0,{\boldsymbol{Z}}_{1\,:\,t}), \qquad \text{\textit{t}, $s\in{{\mathbb{N}}}$}, \end{align*}
\begin{align*} &\bigg(\frac{{\boldsymbol{X}}_{-s\,:\,-1} - {\boldsymbol{a}}_{-s\,:\,-1}(X_0)}{{\boldsymbol{b}}_{-s\,:\,-1}(X_0)},\frac{X_0 - v}{\sigma(v)},\frac{{\boldsymbol{X}}_{1\,:\,t} - {\boldsymbol{a}}_{1\,:\,t}(X_0)}{{\boldsymbol{b}}_{1\,:\,t}(X_0)}\bigg)\,\Big|\,\{X_0>v\} \\\\& {{\,\overset {d }{\longrightarrow }\,}} ({\boldsymbol{Z}}_{-s\,:\,-1},E_0,{\boldsymbol{Z}}_{1\,:\,t}), \qquad \text{\textit{t}, $s\in{{\mathbb{N}}}$}, \end{align*}
where
-
(i)
 $E_0\sim H_0$
is independent of the vector
$E_0\sim H_0$
is independent of the vector
 $({\boldsymbol{Z}}_{-s\,:\,-1}, {\boldsymbol{Z}}_{1\,:\,t})$
for each
$({\boldsymbol{Z}}_{-s\,:\,-1}, {\boldsymbol{Z}}_{1\,:\,t})$
for each
 $s,t\geq 1$
,
$s,t\geq 1$
, -
(ii)
 ${{Z}}_0=0$
a.s.,
${{Z}}_0=0$
a.s.,
 ${\boldsymbol{Z}}_{1\,:\,k-1}\sim G$
, and
${\boldsymbol{Z}}_{1\,:\,k-1}\sim G$
, and \begin{equation*} {{Z}}_{t} = \psi_t^a( {\boldsymbol{Z}}_{t-k\,:\,t-1}) + \psi_t^b( {\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\qquad t=k,k+1,\ldots, \end{equation*}
for independent sequences of i.i.d. random variables
\begin{equation*} {{Z}}_{t} = \psi_t^a( {\boldsymbol{Z}}_{t-k\,:\,t-1}) + \psi_t^b( {\boldsymbol{Z}}_{t-k\,:t-1})\,\varepsilon_t,\qquad t=k,k+1,\ldots, \end{equation*}
for independent sequences of i.i.d. random variables \begin{equation*} {{Z}}_{{-s}} = \psi_{-s}^{a^-}( {\boldsymbol{Z}}_{-s+1\,:\,-s+k}) + \psi_{-s}^{b^-}( {\boldsymbol{Z}}_{-s+1\,:\,-s+k})\,\varepsilon_{-s},\qquad s=1,2,\ldots, \end{equation*}
\begin{equation*} {{Z}}_{{-s}} = \psi_{-s}^{a^-}( {\boldsymbol{Z}}_{-s+1\,:\,-s+k}) + \psi_{-s}^{b^-}( {\boldsymbol{Z}}_{-s+1\,:\,-s+k})\,\varepsilon_{-s},\qquad s=1,2,\ldots, \end{equation*}
 $\{\varepsilon_{-s}\}_{s=1}^{\infty}$
and
$\{\varepsilon_{-s}\}_{s=1}^{\infty}$
and
 $\{\varepsilon_t\}_{t=k}^{\infty}$
, where
$\{\varepsilon_t\}_{t=k}^{\infty}$
, where
 $\varepsilon_{-s} \sim K_A^-$
and
$\varepsilon_{-s} \sim K_A^-$
and
 $\varepsilon_t\sim K_A$
, and
$\varepsilon_t\sim K_A$
, and
 $K_A^{-}$
and
$K_A^{-}$
and
 $K_A$
are defined by the limits (18) and (9), respectively.
$K_A$
are defined by the limits (18) and (9), respectively.
In general there is a relationship between the forward and backward hidden tail chains. When
![]() $k=1$
they are independent, but when
$k=1$
they are independent, but when
![]() $k>1$
and
$k>1$
and
![]() $t+s> k$
,
$t+s> k$
,
![]() ${{Z}}_{t}$
is conditionally independent of
${{Z}}_{t}$
is conditionally independent of
![]() ${{Z}}_{-s}$
given
${{Z}}_{-s}$
given
![]() $({\boldsymbol{Z}}_{-s+1\,:\,-1}, {\boldsymbol{Z}}_{1\,:\,t-1})$
. Hence, given any consecutive block of terms in the back-and forth hidden tail chain of size k, the values before and after this block are independent. We remark that the precise dependence conditions between the forward and backward hidden tail chains have been given for the case where only
$({\boldsymbol{Z}}_{-s+1\,:\,-1}, {\boldsymbol{Z}}_{1\,:\,t-1})$
. Hence, given any consecutive block of terms in the back-and forth hidden tail chain of size k, the values before and after this block are independent. We remark that the precise dependence conditions between the forward and backward hidden tail chains have been given for the case where only
![]() $a_j(x)=x$
and
$a_j(x)=x$
and
![]() $b_j(x)=1$
for all
$b_j(x)=1$
for all
![]() $j\neq 0$
by [Reference Janßen and Segers11]. Subsequently, we focus on the forward hidden tail chain and do not address the inter-connections between the different
$j\neq 0$
by [Reference Janßen and Segers11]. Subsequently, we focus on the forward hidden tail chain and do not address the inter-connections between the different
![]() $a_j(x)$
and
$a_j(x)$
and
![]() $b_j(x)$
for positive and negative j.
$b_j(x)$
for positive and negative j.
Remark 3. When
![]() $k=1$
, by Proposition 1 we can choose, without loss of generality,
$k=1$
, by Proposition 1 we can choose, without loss of generality,
![]() $a(v)=a_1(v)$
and
$a(v)=a_1(v)$
and
![]() $b(v)=b_1(v)$
so that
$b(v)=b_1(v)$
so that
![]() $\psi_1^a(0) = \{a(v) - a_1(v)\}/b_1(v) = 0$
and
$\psi_1^a(0) = \{a(v) - a_1(v)\}/b_1(v) = 0$
and
![]() $\psi_1^b(0)= b(v)/b_1(v) = 1$
. Consequently, (11) implies that
$\psi_1^b(0)= b(v)/b_1(v) = 1$
. Consequently, (11) implies that
![]() ${{Z}}_1 = \varepsilon_1$
and thus, the special case of
${{Z}}_1 = \varepsilon_1$
and thus, the special case of
![]() $k=1$
in Theorem 1 corresponds to the results of [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. The methods of identifying the functions a and b more generally are discussed in Sections 3 and 5.
$k=1$
in Theorem 1 corresponds to the results of [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. The methods of identifying the functions a and b more generally are discussed in Sections 3 and 5.
3. Dependence and recurrence equations under stationarity
3.1. Stationarity and parametric conditional extremes models
For homogeneous Markov chains, the theory presented in Section 2 generalizes to kth-order homogeneous Markov chains (with
![]() $k>1$
) the results for
$k>1$
) the results for
![]() $k=1$
presented in [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. Although working with homogeneous chains embeds the theory in a rather broad setting, it is impossible to explore more details of the results of Theorems 1–4 without imposing further structure, and we do this by assuming stationarity of the Markov chains for the remainder of the paper.
$k=1$
presented in [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. Although working with homogeneous chains embeds the theory in a rather broad setting, it is impossible to explore more details of the results of Theorems 1–4 without imposing further structure, and we do this by assuming stationarity of the Markov chains for the remainder of the paper.
So we now have a common marginal distribution function F over t, with this distribution satisfying Assumption
![]() $A_0$
, unlike previously, when this was assumed only for the variable
$A_0$
, unlike previously, when this was assumed only for the variable
![]() $X_0$
. Specifically, we assume that the stationary Markov chain
$X_0$
. Specifically, we assume that the stationary Markov chain
![]() $\{X_t\}$
has unit-exponential marginal distributions, that is,
$\{X_t\}$
has unit-exponential marginal distributions, that is,
![]() $F(x)\,:\!=\,{{\mathbb{P}}}(X_t \leq x) = (1-\exp({-}x))_+$
, for
$F(x)\,:\!=\,{{\mathbb{P}}}(X_t \leq x) = (1-\exp({-}x))_+$
, for
![]() $t\in {{\mathbb{Z}}}$
, which implies that the limit distribution
$t\in {{\mathbb{Z}}}$
, which implies that the limit distribution
![]() $H_0$
in Assumption 1 is also unit-exponential. This marginal choice gives the clearest mathematical formulation for our needs [Reference Papastathopoulos, Strokorb, Tawn and Butler20], and if a stationary Markov chain
$H_0$
in Assumption 1 is also unit-exponential. This marginal choice gives the clearest mathematical formulation for our needs [Reference Papastathopoulos, Strokorb, Tawn and Butler20], and if a stationary Markov chain
![]() $\{\widetilde{X}_t\}$
has marginal distribution
$\{\widetilde{X}_t\}$
has marginal distribution
![]() $\widetilde{F}\not= F$
then transformation by the probability integral transform
$\widetilde{F}\not= F$
then transformation by the probability integral transform
![]() $X_t=-\log[1-\widetilde{F}(\widetilde{X}_t)]$
, for
$X_t=-\log[1-\widetilde{F}(\widetilde{X}_t)]$
, for
![]() $t\in {{\mathbb{Z}}}$
, gives the required properties. Furthermore, from stationarity we have a time-invariant copula for
$t\in {{\mathbb{Z}}}$
, gives the required properties. Furthermore, from stationarity we have a time-invariant copula for
![]() ${\boldsymbol{X}}_{t-k\, : \, t}$
, for all
${\boldsymbol{X}}_{t-k\, : \, t}$
, for all
![]() $t\in {{\mathbb{Z}}}$
, which together with the marginals can be used to derive the initial conditional distribution
$t\in {{\mathbb{Z}}}$
, which together with the marginals can be used to derive the initial conditional distribution
![]() $F_{1\, : \,k-1 \mid 0}$
and the corresponding
$F_{1\, : \,k-1 \mid 0}$
and the corresponding
![]() $a_t(x)$
and
$a_t(x)$
and
![]() $b_t(x)$
for
$b_t(x)$
for
![]() $t=1,\ldots ,k-1$
, as well as the forms of both
$t=1,\ldots ,k-1$
, as well as the forms of both
![]() $\pi$
and
$\pi$
and
![]() $\pi^-$
, and to show that they are also time-invariant functions.
$\pi^-$
, and to show that they are also time-invariant functions.
With the marginal distribution now fully defined, we look to narrow down the properties of the copula into a single class that covers all of the scenarios discussed in Section 2. This approach is in the style of copula methods, where the assumption of identical margins is typical when identifying the extremal dependence structure of a random vector. In particular, [Reference Heffernan and Tawn9] found that for a broad range of copula models for a random vector
![]() ${\boldsymbol{X}}_{0\,:\,d}$
,
${\boldsymbol{X}}_{0\,:\,d}$
,
![]() $d\in {{\mathbb{N}}}$
, with exponential-tailed random variables, the conditional distribution of the renormalized states
$d\in {{\mathbb{N}}}$
, with exponential-tailed random variables, the conditional distribution of the renormalized states
![]() $\{{\boldsymbol{X}}_{1\,:\,d}-{\boldsymbol{a}}_{1\,:\,d}(X_0)\}/{\boldsymbol{b}}_{1\,:\,d}(X_0)$
, given
$\{{\boldsymbol{X}}_{1\,:\,d}-{\boldsymbol{a}}_{1\,:\,d}(X_0)\}/{\boldsymbol{b}}_{1\,:\,d}(X_0)$
, given
![]() $X_0>v$
, weakly converges to some distribution with non-degenerate margins. They also identified that this convergence typically holds with the normalization functions taking the simple form
$X_0>v$
, weakly converges to some distribution with non-degenerate margins. They also identified that this convergence typically holds with the normalization functions taking the simple form
![]() ${\boldsymbol{a}}_{1\,:\,d}(v)=\boldsymbol{\alpha}_{1\,:\,d}\, v$
and
${\boldsymbol{a}}_{1\,:\,d}(v)=\boldsymbol{\alpha}_{1\,:\,d}\, v$
and
![]() ${\boldsymbol{b}}_{1\,:\,d}(v) = v^{\beta}{\textbf{1}}_d$
, where
${\boldsymbol{b}}_{1\,:\,d}(v) = v^{\beta}{\textbf{1}}_d$
, where
![]() $(\boldsymbol{\alpha}_{1\,:\,d}=(\alpha_1, \ldots ,\alpha_d),\beta) \in[0,1]^{d}\times[0,1)$
. The parameters
$(\boldsymbol{\alpha}_{1\,:\,d}=(\alpha_1, \ldots ,\alpha_d),\beta) \in[0,1]^{d}\times[0,1)$
. The parameters
![]() $\alpha_t$
and
$\alpha_t$
and
![]() $\beta$
have a simple interpretation and control the strength of extremal association between the variables
$\beta$
have a simple interpretation and control the strength of extremal association between the variables
![]() $X_0$
and
$X_0$
and
![]() $X_t$
, for
$X_t$
, for
![]() $t=1,\ldots,d$
. Informally, in the presence of an extreme event
$t=1,\ldots,d$
. Informally, in the presence of an extreme event
![]() $X_0$
with
$X_0$
with
![]() $X_0 > v$
and v sufficiently large, we may then think of
$X_0 > v$
and v sufficiently large, we may then think of
![]() $X_t$
as
$X_t$
as
![]() $X_t = \alpha_t X_0 + X_0^\beta \,{{Z}}_t$
where
$X_t = \alpha_t X_0 + X_0^\beta \,{{Z}}_t$
where
![]() ${{Z}}_t$
has a non-degenerate distribution. Thus,
${{Z}}_t$
has a non-degenerate distribution. Thus,
![]() $\alpha_t$
and
$\alpha_t$
and
![]() $\beta$
are slope and scale parameters, respectively, with larger values of
$\beta$
are slope and scale parameters, respectively, with larger values of
![]() $\alpha_t$
indicating stronger linear dependence between
$\alpha_t$
indicating stronger linear dependence between
![]() $X_t$
and the big values of
$X_t$
and the big values of
![]() $X_0$
, and, for fixed
$X_0$
, and, for fixed
![]() $\alpha_t$
, the larger values of
$\alpha_t$
, the larger values of
![]() $\beta$
indicating a more diffuse distribution for
$\beta$
indicating a more diffuse distribution for
![]() $X_t\mid X_0 > v$
. The links to Section 2 and full pairwise asymptotically dependent and full pairwise asymptotically independent kth-order Markov processes can now be made much clearer. Specifically,
$X_t\mid X_0 > v$
. The links to Section 2 and full pairwise asymptotically dependent and full pairwise asymptotically independent kth-order Markov processes can now be made much clearer. Specifically,
![]() $\alpha_t\in (0,1]$
for all
$\alpha_t\in (0,1]$
for all
![]() $t=1, \ldots ,k$
corresponds to a family of copulas satisfying the conditions of Section 2.3 with the special case of
$t=1, \ldots ,k$
corresponds to a family of copulas satisfying the conditions of Section 2.3 with the special case of
![]() $\alpha_t=1$
and
$\alpha_t=1$
and
![]() $\beta=0$
for all
$\beta=0$
for all
![]() $t=1, \ldots ,k-1$
being a full pairwise asymptotically dependent Markov chain, with
$t=1, \ldots ,k-1$
being a full pairwise asymptotically dependent Markov chain, with
![]() $\chi_t >0$
for
$\chi_t >0$
for
![]() $t=1,\ldots, k-1$
, so it only arises as a special case in Section 2.3. In contrast, full pairwise asymptotically independent processes arise as a broad class in Section 2.3 and all scenarios in Sections 2.4 and 2.5. Specifically, we have pairwise asymptotic independence in Section 2.3 when
$t=1,\ldots, k-1$
, so it only arises as a special case in Section 2.3. In contrast, full pairwise asymptotically independent processes arise as a broad class in Section 2.3 and all scenarios in Sections 2.4 and 2.5. Specifically, we have pairwise asymptotic independence in Section 2.3 when
![]() $\alpha_t\in [0,1)$
for all
$\alpha_t\in [0,1)$
for all
![]() $t=1,\ldots, k-1$
, in Section 2.4 when
$t=1,\ldots, k-1$
, in Section 2.4 when
![]() $\alpha_t=0$
for all
$\alpha_t=0$
for all
![]() $t=1, \ldots ,k-1$
and
$t=1, \ldots ,k-1$
and
![]() $\beta\in (0,1)$
, and in Section 2.5 when
$\beta\in (0,1)$
, and in Section 2.5 when
![]() $\alpha_t=0$
for all
$\alpha_t=0$
for all
![]() $t=1, \ldots ,k-1$
and
$t=1, \ldots ,k-1$
and
![]() $\beta=0$
. Here we assume that the formulation of [Reference Heffernan and Tawn9] holds for the initial conditional distribution, i.e. giving
$\beta=0$
. Here we assume that the formulation of [Reference Heffernan and Tawn9] holds for the initial conditional distribution, i.e. giving
![]() $\alpha_t$
for
$\alpha_t$
for
![]() $t=1, \ldots ,k-1$
and
$t=1, \ldots ,k-1$
and
![]() $\beta$
, and we focus on deriving the structure of
$\beta$
, and we focus on deriving the structure of
![]() $\alpha_t$
and
$\alpha_t$
and
![]() $\beta_t$
for all
$\beta_t$
for all
![]() $t\ge k$
and the stochastic recurrence properties of the hidden tail chains for both full pairwise asymptotically dependent and full pairwise asymptotically independent kth-order stationary Markov chains.
$t\ge k$
and the stochastic recurrence properties of the hidden tail chains for both full pairwise asymptotically dependent and full pairwise asymptotically independent kth-order stationary Markov chains.
3.2. Full pairwise asymptotically dependent Markov chains
Corollary 1. (Full pairwise asymptotically dependent Markov chains).
Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose that Assumption 2 holds with
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose that Assumption 2 holds with
![]() $a_t(x)=x$
and
$a_t(x)=x$
and
![]() $b_t(x)=1$
, for
$b_t(x)=1$
, for
![]() $t=1,\ldots,k-1$
. Suppose further that Assumption 3 holds with functions a and b, defined there, such that a is non-zero and continuous, and
$t=1,\ldots,k-1$
. Suppose further that Assumption 3 holds with functions a and b, defined there, such that a is non-zero and continuous, and
![]() $\exp\{a( \log {\boldsymbol{x}} )\}$
,
$\exp\{a( \log {\boldsymbol{x}} )\}$
,
![]() ${\boldsymbol{x}} \in {{{\mathbb{R}}}}^k_+$
, is 1-homogeneous; that is,
${\boldsymbol{x}} \in {{{\mathbb{R}}}}^k_+$
, is 1-homogeneous; that is,
with
![]() $a({\textbf{0}}_k) \leq 0$
and
$a({\textbf{0}}_k) \leq 0$
and
![]() $b(\cdot)\equiv 1$
. Then the convergence (10) holds with
$b(\cdot)\equiv 1$
. Then the convergence (10) holds with
![]() $a_t(x)=x$
and
$a_t(x)=x$
and
![]() $b_t(x)=1$
for
$b_t(x)=1$
for
![]() $t\geq k$
, and
$t\geq k$
, and
for a sequence
![]() $\{\varepsilon_{t}\}_{t=k}^\infty$
of i.i.d. random variables with a distribution
$\{\varepsilon_{t}\}_{t=k}^\infty$
of i.i.d. random variables with a distribution
![]() $K_A$
, as defined in the limit (9), supported on
$K_A$
, as defined in the limit (9), supported on
![]() ${{{\mathbb{R}}}}$
. Furthermore,
${{{\mathbb{R}}}}$
. Furthermore,
![]() $\mathbb{E}(Z_t) < 0$
for all
$\mathbb{E}(Z_t) < 0$
for all
![]() $t\geq 1$
.
$t\geq 1$
.
So in terms of the parameters of [Reference Heffernan and Tawn9], here
![]() $\alpha_t=1$
and
$\alpha_t=1$
and
![]() $\beta_t=0$
for all
$\beta_t=0$
for all
![]() $t\in {{\mathbb{Z}}}$
, and consequently the process is pairwise asymptotically dependent for
$t\in {{\mathbb{Z}}}$
, and consequently the process is pairwise asymptotically dependent for
![]() $(X_0,X_t)$
, i.e.,
$(X_0,X_t)$
, i.e.,
![]() $\chi_t>0$
, for any
$\chi_t>0$
, for any
![]() $t\ge k$
. Although this gives that
$t\ge k$
. Although this gives that
![]() $a_t(x)=x$
and
$a_t(x)=x$
and
![]() $b_t(x)=1$
for all
$b_t(x)=1$
for all
![]() $t\geq 1$
, suggesting that asymptotically dependent Markov chains stay extreme forever after witnessing an extreme value, they do in fact return to the body of the distribution thanks to the negative drift of the tail chain; that is,
$t\geq 1$
, suggesting that asymptotically dependent Markov chains stay extreme forever after witnessing an extreme value, they do in fact return to the body of the distribution thanks to the negative drift of the tail chain; that is,
![]() $\mathbb{E}({{Z}}_t) < 0$
for all
$\mathbb{E}({{Z}}_t) < 0$
for all
![]() $t\geq 1$
, which ensures that the Markov chain will return to the body regardless of the behaviour of the norming functions. Corollary 1 refines our understanding of full pairwise asymptotically dependent Markov chains by identifying a class of update functions a whose defining property is (19), also known as topical maps, which can be regarded as nonlinear generalizations of row-stochastic matrices [Reference Lemmens and Nussbaum17].
$t\geq 1$
, which ensures that the Markov chain will return to the body regardless of the behaviour of the norming functions. Corollary 1 refines our understanding of full pairwise asymptotically dependent Markov chains by identifying a class of update functions a whose defining property is (19), also known as topical maps, which can be regarded as nonlinear generalizations of row-stochastic matrices [Reference Lemmens and Nussbaum17].
3.3. Full pairwise asymptotically independent Markov chains
As there are different types of dependence that lead to full pairwise asymptotic independent behaviour, we separate our findings into Corollaries 2 and 3, which correspond to the conditions of Sections 2.3 and 2.4, respectively.
Corollary 2. (Full pairwise asymptotically independent Markov chains with location and scale norming.)
Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose Assumption 2 holds with
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose Assumption 2 holds with
![]() $a_t(v)=\alpha_t\,v$
,
$a_t(v)=\alpha_t\,v$
,
![]() $\alpha_t \in (0,1)$
and
$\alpha_t \in (0,1)$
and
![]() $b_t(v) = v^{\beta_t}$
,
$b_t(v) = v^{\beta_t}$
,
![]() $\beta_t = \beta \in [0,1)$
, for
$\beta_t = \beta \in [0,1)$
, for
![]() $t=1,\ldots,k-1$
. Suppose that Assumption 3 holds with the function a being a twice continuously differentiable, order-preserving 1-homogeneous function, with
$t=1,\ldots,k-1$
. Suppose that Assumption 3 holds with the function a being a twice continuously differentiable, order-preserving 1-homogeneous function, with
![]() $a({\textbf{1}}_k)< 1$
, and the function b being
$a({\textbf{1}}_k)< 1$
, and the function b being
![]() $\beta$
-homogeneous when
$\beta$
-homogeneous when
![]() $\beta\in (0,1)$
and unity when
$\beta\in (0,1)$
and unity when
![]() $\beta = 0$
. Then the convergence (10) holds with, for
$\beta = 0$
. Then the convergence (10) holds with, for
![]() $t\ge k$
,
$t\ge k$
,
![]() $a_t(v)=\alpha_t \, v$
and
$a_t(v)=\alpha_t \, v$
and
![]() $b_t(v)=v^{\beta}$
, where
$b_t(v)=v^{\beta}$
, where
with
![]() $\alpha_t\in (0,1)$
for all
$\alpha_t\in (0,1)$
for all
![]() $t\ge k$
, and
$t\ge k$
, and
for a sequence
![]() $\{\varepsilon_t\}_{t=k}^\infty$
of i.i.d. random variables from a non-degenerate distribution
$\{\varepsilon_t\}_{t=k}^\infty$
of i.i.d. random variables from a non-degenerate distribution
![]() $K_A$
, defined in the limit (9), on
$K_A$
, defined in the limit (9), on
![]() ${{{\mathbb{R}}}}$
. Consequently, the process is pairwise asymptotically independent for
${{{\mathbb{R}}}}$
. Consequently, the process is pairwise asymptotically independent for
![]() $(X_0,X_t)$
, i.e.
$(X_0,X_t)$
, i.e.
![]() $\chi_t=0$
for any
$\chi_t=0$
for any
![]() $t\ge k$
, and
$t\ge k$
, and
![]() $\alpha_t \to 0$
as
$\alpha_t \to 0$
as
![]() $t\to\infty$
.
$t\to\infty$
.
In Section 4 we are able to explicitly solve the recurrence equation (20) for a flexible parametric class of the function a, and find a geometric decay to zero in
![]() $\alpha_t$
as t increases. Even for an arbitrary functional a satisfying the weak assumptions of Corollary 2, considerable insight into the behaviour of the hidden tail chain is achieved from Corollary 2. It shows that the norming functions
$\alpha_t$
as t increases. Even for an arbitrary functional a satisfying the weak assumptions of Corollary 2, considerable insight into the behaviour of the hidden tail chain is achieved from Corollary 2. It shows that the norming functions
![]() $a_t$
,
$a_t$
,
![]() $t=k,k+1,\ldots,$
have a particularly neat structure, not least
$t=k,k+1,\ldots,$
have a particularly neat structure, not least
![]() $a_t(X_0)=\alpha_t\,X_0$
, where
$a_t(X_0)=\alpha_t\,X_0$
, where
![]() $\alpha_t$
is determined by the recurrence equation (20) of the k previous values
$\alpha_t$
is determined by the recurrence equation (20) of the k previous values
![]() $\boldsymbol{\alpha}_{t-k\,:\,t-1}$
through the 1-homogeneous function a.
$\boldsymbol{\alpha}_{t-k\,:\,t-1}$
through the 1-homogeneous function a.
Since Corollary 2 gives that
![]() $\alpha_t\to 0$
as
$\alpha_t\to 0$
as
![]() $t\to \infty$
, this leads to there eventually being no location-norming in the limit, which is consistent with the independence case. However, for practical usage we need to consider the limit at
$t\to \infty$
, this leads to there eventually being no location-norming in the limit, which is consistent with the independence case. However, for practical usage we need to consider the limit at
![]() $t\rightarrow \infty$
whilst also allowing the level of extremity of
$t\rightarrow \infty$
whilst also allowing the level of extremity of
![]() $X_0$
to increase, i.e. the value
$X_0$
to increase, i.e. the value
![]() $v\rightarrow \infty$
. We address these issues for the cases
$v\rightarrow \infty$
. We address these issues for the cases
![]() $\beta=0$
and
$\beta=0$
and
![]() $\beta\in (0,1)$
. When
$\beta\in (0,1)$
. When
![]() $\beta=0$
, the behaviour of the forward Markov chain as
$\beta=0$
, the behaviour of the forward Markov chain as
![]() $t\to \infty$
and
$t\to \infty$
and
![]() $v\to \infty$
is almost entirely given by Corollary 2, as
$v\to \infty$
is almost entirely given by Corollary 2, as
![]() $X_t|\{X_0=v\} = \alpha_t \,v + Z_t +o_p(1)$
. If we can suitably link
$X_t|\{X_0=v\} = \alpha_t \,v + Z_t +o_p(1)$
. If we can suitably link
![]() $t\rightarrow \infty$
with
$t\rightarrow \infty$
with
![]() $v\rightarrow \infty$
, the location term
$v\rightarrow \infty$
, the location term
![]() $\alpha_t\,v$
will tend to zero and
$\alpha_t\,v$
will tend to zero and
![]() $X_t$
will converge to the process
$X_t$
will converge to the process
![]() $\{Z_t\}$
, which is a non-degenerate autoregressive process. So, with such combined limiting operations, we have that
$\{Z_t\}$
, which is a non-degenerate autoregressive process. So, with such combined limiting operations, we have that
![]() $X_t\mid \{X_0=v\}$
returns to the body of the distribution as
$X_t\mid \{X_0=v\}$
returns to the body of the distribution as
![]() $t\to \infty$
, becoming independent of
$t\to \infty$
, becoming independent of
![]() $X_0$
. Here, if there were a constant
$X_0$
. Here, if there were a constant
![]() $A\in (0,1)$
with
$A\in (0,1)$
with
![]() $\alpha_t\sim A^t$
as
$\alpha_t\sim A^t$
as
![]() $t\rightarrow \infty$
, i.e. the
$t\rightarrow \infty$
, i.e. the
![]() $\alpha_t$
exhibit geometric decay, as in the parametric class for a in Section 4, then we would need
$\alpha_t$
exhibit geometric decay, as in the parametric class for a in Section 4, then we would need
![]() $t/\log(v)\rightarrow \infty$
as
$t/\log(v)\rightarrow \infty$
as
![]() $v\rightarrow \infty$
for this result to hold. When
$v\rightarrow \infty$
for this result to hold. When
![]() $0<\beta<1$
the limiting behaviour of the forward hidden chain
$0<\beta<1$
the limiting behaviour of the forward hidden chain
![]() $X_t|\{X_0=v\}$
as
$X_t|\{X_0=v\}$
as
![]() $t\to \infty$
is only partially implied by Corollary 2. This is because
$t\to \infty$
is only partially implied by Corollary 2. This is because
![]() $Z_t{{\,\overset {p }{\longrightarrow }\,}} 0$
, since both the location and the scale terms of
$Z_t{{\,\overset {p }{\longrightarrow }\,}} 0$
, since both the location and the scale terms of
![]() $\varepsilon_t$
in (21) tend to zero, but its scaling
$\varepsilon_t$
in (21) tend to zero, but its scaling
![]() $v^{\beta}$
tends to infinity. Consequently, the limiting behaviour is determined by the relative speed of convergence of
$v^{\beta}$
tends to infinity. Consequently, the limiting behaviour is determined by the relative speed of convergence of
![]() $\alpha_t\, v\rightarrow 0$
and
$\alpha_t\, v\rightarrow 0$
and
![]() $v^{\beta}\,Z_t{{\,\overset {p }{\longrightarrow }\,}} 0$
if we link the growth rate of t to that of v.
$v^{\beta}\,Z_t{{\,\overset {p }{\longrightarrow }\,}} 0$
if we link the growth rate of t to that of v.
In general we can view the recurrence relation in (20) as the parallel of the Yule–Walker equations; hence we term them the extremal Yule–Walker equations. The Yule–Walker equations provide a recurrence relation for the autocorrelation function in standard time series that is used to determine the dependence properties of a linear Markov process. For a kth-order linear Markov process
![]() $Y_t = \sum_{i=1}^k \phi_i\, Y_{t-k+i-1}+\eta_t$
with
$Y_t = \sum_{i=1}^k \phi_i\, Y_{t-k+i-1}+\eta_t$
with
![]() $\{\eta_t\}_{t=-\infty}^\infty$
a sequence of zero-mean, common-finite-variance, and uncorrelated random variables, where the set of regression parameters
$\{\eta_t\}_{t=-\infty}^\infty$
a sequence of zero-mean, common-finite-variance, and uncorrelated random variables, where the set of regression parameters
![]() $\phi_1,\ldots, \phi_k$
are real-valued constants such that the characteristic polynomial
$\phi_1,\ldots, \phi_k$
are real-valued constants such that the characteristic polynomial
![]() $1-\phi_k\, z - \phi_{k-1}\, z^2- \cdots - \phi_1\, z^k\neq 0$
on
$1-\phi_k\, z - \phi_{k-1}\, z^2- \cdots - \phi_1\, z^k\neq 0$
on
![]() $\{z\in \mathbb{C}\,:\, \lvert z \lvert \leq 1\}$
, the Yule–Walker equations relate the autocorrelation function of the process
$\{z\in \mathbb{C}\,:\, \lvert z \lvert \leq 1\}$
, the Yule–Walker equations relate the autocorrelation function of the process
![]() $\rho_t = \text{cor}(Y_{s-t}, Y_s)$
at lag t with the regression parameters
$\rho_t = \text{cor}(Y_{s-t}, Y_s)$
at lag t with the regression parameters
![]() $\phi_1,\ldots, \phi_k$
and the k lagged autocorrelations according to
$\phi_1,\ldots, \phi_k$
and the k lagged autocorrelations according to
![]() $\rho_t = \sum_{i=1}^k \phi_{i} \,\rho_{t-i}$
,
$\rho_t = \sum_{i=1}^k \phi_{i} \,\rho_{t-i}$
,
![]() $t \in {{\mathbb{Z}}}$
. The sequence
$t \in {{\mathbb{Z}}}$
. The sequence
![]() $\{\alpha_t\}$
has a similar structure for extremes via the recurrence (20).
$\{\alpha_t\}$
has a similar structure for extremes via the recurrence (20).
In Corollary 2 we exclude the case
![]() $\beta < 0$
considered by [Reference Heffernan and Tawn9], which corresponds to the case where location-only normalization gives limits that are degenerate, with all limiting mass at
$\beta < 0$
considered by [Reference Heffernan and Tawn9], which corresponds to the case where location-only normalization gives limits that are degenerate, with all limiting mass at
![]() $\{0\}$
. For simplicity, the theory developed in this paper deals only with positive extremal association in Markov chains, and hence, in Corollary 2, the case where
$\{0\}$
. For simplicity, the theory developed in this paper deals only with positive extremal association in Markov chains, and hence, in Corollary 2, the case where
![]() $X_0$
and
$X_0$
and
![]() $X_t$
exhibit negative extremal association is also ruled out. We note, however, that this latter case potentially can be accommodated by suitable transformations of the marginal distributions, e.g. by standardizing margins to standard Laplace distributions and then allowing
$X_t$
exhibit negative extremal association is also ruled out. We note, however, that this latter case potentially can be accommodated by suitable transformations of the marginal distributions, e.g. by standardizing margins to standard Laplace distributions and then allowing
![]() $\alpha_t <0$
; see for example [Reference Keef, Papastathopoulos and Tawn13] and [Reference Papastathopoulos, Strokorb, Tawn and Butler20 Theorem 3]. However, some modifications in the conditions will be required to address the complications that some arguments will tend to
$\alpha_t <0$
; see for example [Reference Keef, Papastathopoulos and Tawn13] and [Reference Papastathopoulos, Strokorb, Tawn and Butler20 Theorem 3]. However, some modifications in the conditions will be required to address the complications that some arguments will tend to
![]() $-\infty$
whilst the conditioning variable will still go to
$-\infty$
whilst the conditioning variable will still go to
![]() $\infty$
.
$\infty$
.
Corollary 3. (Full pairwise asymptotically independent Markov chains with only scale norming) Let
![]() $\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose that Assumption 4 holds with
$\{X_t\,:\,t\in {{\mathbb{Z}}}\}$
be a kth-order stationary Markov chain with unit-exponential margins. Suppose that Assumption 4 holds with
![]() $b_t(x) = x^{\beta}$
,
$b_t(x) = x^{\beta}$
,
![]() $\beta \in (0,1)$
, for
$\beta \in (0,1)$
, for
![]() $t=1,\ldots,k-1$
. Suppose further that Assumption 5 holds with the function b being continuous and
$t=1,\ldots,k-1$
. Suppose further that Assumption 5 holds with the function b being continuous and
![]() $\beta$
-homogeneous. Then the convergence (14) holds with
$\beta$
-homogeneous. Then the convergence (14) holds with
![]() $b_t(x)=x^{\beta_t}$
,
$b_t(x)=x^{\beta_t}$
,
![]() $\beta_t\in (0,1)$
,
$\beta_t\in (0,1)$
,
![]() $t\geq k$
, where
$t\geq k$
, where
![]() $\beta_t$
satisfies the recurrence relation
$\beta_t$
satisfies the recurrence relation
![]() $\log \beta_t = \log \beta + \log(\max_{i=1,\ldots,k}\beta_{t-i})$
, with
$\log \beta_t = \log \beta + \log(\max_{i=1,\ldots,k}\beta_{t-i})$
, with
![]() $\beta_1=\ldots =\beta_{k-1}=\beta$
. This gives the solution
$\beta_1=\ldots =\beta_{k-1}=\beta$
. This gives the solution
where
![]() $\lfloor x \rfloor$
denotes the integer part of x. It follows that
$\lfloor x \rfloor$
denotes the integer part of x. It follows that
![]() $\beta_t\in (0,1)$
for all
$\beta_t\in (0,1)$
for all
![]() $t\ge k$
and that
$t\ge k$
and that
![]() $\beta_t \to 0$
as
$\beta_t \to 0$
as
![]() $t\to \infty$
. Also, for
$t\to \infty$
. Also, for
![]() $t\geq k$
we have
$t\geq k$
we have
 \begin{align*} {{Z}}_{t} = \left\{ \begin{array}{l} b({{Z}}_{t-k}, {\textbf{0}}_{k-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t)=0$},\\[2pt] b({{Z}}_{t-k},\ldots, {{Z}}_{t-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t) = 1$},\\[2pt] b({{Z}}_{t-k},\ldots, {{Z}}_{t-j}, {\textbf{0}}_{j-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t) = j \in \{2,\ldots,k-1\}$}, \end{array} \right. \end{align*}
\begin{align*} {{Z}}_{t} = \left\{ \begin{array}{l} b({{Z}}_{t-k}, {\textbf{0}}_{k-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t)=0$},\\[2pt] b({{Z}}_{t-k},\ldots, {{Z}}_{t-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t) = 1$},\\[2pt] b({{Z}}_{t-k},\ldots, {{Z}}_{t-j}, {\textbf{0}}_{j-1}) \,\varepsilon_{t} \quad \text{when $\text{mod}_k(t) = j \in \{2,\ldots,k-1\}$}, \end{array} \right. \end{align*}
for a sequence
![]() $\{\varepsilon_t\}_{t=k}^\infty$
of i.i.d. random variables with distribution
$\{\varepsilon_t\}_{t=k}^\infty$
of i.i.d. random variables with distribution
![]() $K_B$
, defined by the limit (13), supported on
$K_B$
, defined by the limit (13), supported on
![]() ${{{\mathbb{R}}}}_+$
and
${{{\mathbb{R}}}}_+$
and
![]() ${{Z}}_0=1$
a.s. As a consequence, the process is pairwise asymptotically independent for
${{Z}}_0=1$
a.s. As a consequence, the process is pairwise asymptotically independent for
![]() $(X_0,X_t)$
, i.e.
$(X_0,X_t)$
, i.e.
![]() $\chi_t=0$
, for any
$\chi_t=0$
, for any
![]() $t\ge k$
.
$t\ge k$
.
In contrast to Corollary 2, where the location parameter
![]() $\alpha_t$
changed with t, here it is the power parameter
$\alpha_t$
changed with t, here it is the power parameter
![]() $\beta_t$
of the scale function that is decaying. As with Corollary 2 we find a form of geometric decay in the dependence parameters
$\beta_t$
of the scale function that is decaying. As with Corollary 2 we find a form of geometric decay in the dependence parameters
![]() $\beta_t$
as t increases, leading eventually to extremal independence (
$\beta_t$
as t increases, leading eventually to extremal independence (
![]() $\alpha_t=0$
and
$\alpha_t=0$
and
![]() $\beta_t\to 0$
) in the limit as
$\beta_t\to 0$
) in the limit as
![]() $t\to\infty$
, so that
$t\to\infty$
, so that
![]() $X_t$
returns to the body of the distribution as it becomes independent of
$X_t$
returns to the body of the distribution as it becomes independent of
![]() $X_0$
. In particular,
$X_0$
. In particular,
![]() $\beta_t$
decays geometrically to 0 stepwise, with steps at every k lags. At time t the resulting hidden tail chain depends only on the last j values, with
$\beta_t$
decays geometrically to 0 stepwise, with steps at every k lags. At time t the resulting hidden tail chain depends only on the last j values, with
![]() $j = \text{mod}_k(t)$
.
$j = \text{mod}_k(t)$
.
4. A class of recurrence relations for dependence parameters in asymptotically independent Markov chains with closed-form solutions
The results of Section 3 provide insight into the form of the norming and updating functions of Theorems 1 and 2, not least for asymptotically independent Markov chains where
![]() $(\alpha_t,\beta_t)\neq (1,0)$
for all
$(\alpha_t,\beta_t)\neq (1,0)$
for all
![]() $t > 0$
. A precise formulation of the location and scale parameters
$t > 0$
. A precise formulation of the location and scale parameters
![]() $\alpha_t$
and
$\alpha_t$
and
![]() $\beta_t$
for
$\beta_t$
for
![]() $t\geq k$
, however, depends on the forms of functionals
$t\geq k$
, however, depends on the forms of functionals
![]() $a(\cdot)$
and
$a(\cdot)$
and
![]() $b(\cdot)$
which are opaque even when these are assumed to be homogeneous functionals. Motivated by examples considered in Section 5.3, here we give an explicit characterization of the solution to the extremal Yule–Walker equations (20) in Corollary 2 for a parsimonious parametric subclass of functionals
$b(\cdot)$
which are opaque even when these are assumed to be homogeneous functionals. Motivated by examples considered in Section 5.3, here we give an explicit characterization of the solution to the extremal Yule–Walker equations (20) in Corollary 2 for a parsimonious parametric subclass of functionals
![]() $a_{\mathcal{M}}$
, of a, which embeds many of the examples of Section 5.
$a_{\mathcal{M}}$
, of a, which embeds many of the examples of Section 5.
For
![]() ${\boldsymbol{x}}=(x_1, \ldots ,x_k)\in {{{\mathbb{R}}}}_+^k$
,
${\boldsymbol{x}}=(x_1, \ldots ,x_k)\in {{{\mathbb{R}}}}_+^k$
,
![]() $0< c < 1$
,
$0< c < 1$
,
![]() $\delta \in \overline{{{{\mathbb{R}}}}}$
, and
$\delta \in \overline{{{{\mathbb{R}}}}}$
, and
![]() $(\gamma_1,\ldots, \gamma_k) \in {{\Delta}}^{k-1}$
with
$(\gamma_1,\ldots, \gamma_k) \in {{\Delta}}^{k-1}$
with
![]() $\min_{j=1,\ldots,k} (\gamma_j)> 0$
, consider the function
$\min_{j=1,\ldots,k} (\gamma_j)> 0$
, consider the function
![]() $a_{\mathcal{M}}:{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
defined by
$a_{\mathcal{M}}:{{{\mathbb{R}}}}_+^k \to {{{\mathbb{R}}}}_+$
defined by
Here
![]() $a_{\mathcal{M}}$
satisfies the conditions of Corollary 2, as it is order-preserving and 1-homogeneous, and the bound on c ensures that
$a_{\mathcal{M}}$
satisfies the conditions of Corollary 2, as it is order-preserving and 1-homogeneous, and the bound on c ensures that
![]() $a({\textbf{1}}_k)<1$
. The functional
$a({\textbf{1}}_k)<1$
. The functional
![]() $a_{\mathcal{M}}$
is continuous in
$a_{\mathcal{M}}$
is continuous in
![]() $\delta \in \overline{{{{\mathbb{R}}}}}$
, though its values at
$\delta \in \overline{{{{\mathbb{R}}}}}$
, though its values at
![]() $\delta=-\infty, 0, \infty$
need careful treatment as they are not immediately apparent from (22). Specifically,
$\delta=-\infty, 0, \infty$
need careful treatment as they are not immediately apparent from (22). Specifically,
and
Proposition 2. Consider the function
![]() $a_{\mathcal{M}}$
defined by (22). Suppose that the
$a_{\mathcal{M}}$
defined by (22). Suppose that the
![]() $s\in{{\mathbb{N}}}$
distinct (possibly complex) roots of the characteristic polynomial
$s\in{{\mathbb{N}}}$
distinct (possibly complex) roots of the characteristic polynomial
are
![]() $r_1,\ldots,r_s$
with multiplicities
$r_1,\ldots,r_s$
with multiplicities
![]() $m_1,\ldots,m_s$
,
$m_1,\ldots,m_s$
,
![]() $\sum_i m_i = k$
. Then the solution of the recurrence relation (20) with
$\sum_i m_i = k$
. Then the solution of the recurrence relation (20) with
![]() $a({\boldsymbol{x}}) = a_{\mathcal{M}}({\boldsymbol{x}})$
for all
$a({\boldsymbol{x}}) = a_{\mathcal{M}}({\boldsymbol{x}})$
for all
![]() ${\boldsymbol{x}}\in{{{\mathbb{R}}}}_+^k$
, subject to the initial condition
${\boldsymbol{x}}\in{{{\mathbb{R}}}}_+^k$
, subject to the initial condition
![]() $(\alpha_1,\ldots,\alpha_{k-1}) \in (0,1)^{k-1}$
, is
$(\alpha_1,\ldots,\alpha_{k-1}) \in (0,1)^{k-1}$
, is
where the constants
![]() $C_{i0},\ldots,C_{i,m_i-1}$
,
$C_{i0},\ldots,C_{i,m_i-1}$
,
![]() $i=1,\ldots,s$
, are uniquely determined by the initial condition via the system of equations
$i=1,\ldots,s$
, are uniquely determined by the initial condition via the system of equations
![]() $\alpha_0=1$
and
$\alpha_0=1$
and
From Corollary 2, it follows that the sequence
![]() $\{\alpha_t\}$
in Proposition 2 satisfies
$\{\alpha_t\}$
in Proposition 2 satisfies
![]() $\alpha_t\to 0$
as
$\alpha_t\to 0$
as
![]() $t\to \infty$
. Let
$t\to \infty$
. Let
![]() $I_r=\{I\in\{1,\ldots,s\}\,:\,|r_I|=\max_{i=1,\ldots,s}|r_i|\}$
. Under the assumption that
$I_r=\{I\in\{1,\ldots,s\}\,:\,|r_I|=\max_{i=1,\ldots,s}|r_i|\}$
. Under the assumption that
![]() $|I_r|=1$
, we have that
$|I_r|=1$
, we have that
![]() $\alpha_t$
satisfies
$\alpha_t$
satisfies
![]() $\alpha_{t} \sim C_{I,m_I-1}\,t^{(m_I-1)/\delta} r_I^{t/\delta} \to0$
,
$\alpha_{t} \sim C_{I,m_I-1}\,t^{(m_I-1)/\delta} r_I^{t/\delta} \to0$
,
![]() $I\in I_r$
,
$I\in I_r$
,
![]() $\delta \in {{{\mathbb{R}}}} {{\setminus}} \{0\}$
, as
$\delta \in {{{\mathbb{R}}}} {{\setminus}} \{0\}$
, as
![]() $t\to \infty$
.
$t\to \infty$
.
Remark 4. Although
![]() $a_{\mathcal{M}}$
in (22) is defined for any
$a_{\mathcal{M}}$
in (22) is defined for any
![]() $\delta \in \overline{{{{\mathbb{R}}}}}$
, it is not evident from Proposition 2 what form the solution takes when
$\delta \in \overline{{{{\mathbb{R}}}}}$
, it is not evident from Proposition 2 what form the solution takes when
![]() $\delta=0$
or when
$\delta=0$
or when
![]() $\delta=\pm\infty$
. These cases are considered separately below.
$\delta=\pm\infty$
. These cases are considered separately below.
Case
![]() $\delta \to 0$
: A logarithmic transformation in the limit (23) results in the linear non-homogeneous recurrence relation
$\delta \to 0$
: A logarithmic transformation in the limit (23) results in the linear non-homogeneous recurrence relation
Suppose that the
![]() $s\in{{\mathbb{N}}}$
distinct (possibly complex) roots of the characteristic polynomial
$s\in{{\mathbb{N}}}$
distinct (possibly complex) roots of the characteristic polynomial
are
![]() $r_1,\ldots,r_s$
with multiplicities
$r_1,\ldots,r_s$
with multiplicities
![]() $m_1,\ldots,m_s$
,
$m_1,\ldots,m_s$
,
![]() $\sum m_i=k$
. Then the solution of the recurrence (20) is
$\sum m_i=k$
. Then the solution of the recurrence (20) is
 \begin{align*} \alpha_t = \exp\Bigg\{\sum_{i=1}^s \big( C_{i0} + C_{i1}\,t + \cdots + C_{i,m_i-1} t^{m_i-1}\big) \,r_i^t + \frac{c}{\gamma_1+ 2\gamma_2 + \cdots + k\gamma_k} t\Bigg\},\end{align*}
\begin{align*} \alpha_t = \exp\Bigg\{\sum_{i=1}^s \big( C_{i0} + C_{i1}\,t + \cdots + C_{i,m_i-1} t^{m_i-1}\big) \,r_i^t + \frac{c}{\gamma_1+ 2\gamma_2 + \cdots + k\gamma_k} t\Bigg\},\end{align*}
for
![]() $t=k,k+1,\ldots$
, where the constants
$t=k,k+1,\ldots$
, where the constants
![]() $C_{i0},\ldots,C_{i,m_i-1}$
,
$C_{i0},\ldots,C_{i,m_i-1}$
,
![]() $i=1,\ldots,s$
, are uniquely determined by the system of equations
$i=1,\ldots,s$
, are uniquely determined by the system of equations
 \begin{align*} \alpha_t = \exp\Bigg\{\sum_{i=1}^s \big( C_{i0} + C_{i1}\,t +\cdots + C_{i,m_i-1} t^{m_i-1}\big) \,r_i^t+ \frac{c}{\gamma_1+ 2\gamma_2 + \cdots + k\gamma_k} t \Bigg\},\end{align*}
\begin{align*} \alpha_t = \exp\Bigg\{\sum_{i=1}^s \big( C_{i0} + C_{i1}\,t +\cdots + C_{i,m_i-1} t^{m_i-1}\big) \,r_i^t+ \frac{c}{\gamma_1+ 2\gamma_2 + \cdots + k\gamma_k} t \Bigg\},\end{align*}
for
![]() $t=0,\ldots,k-1$
, with
$t=0,\ldots,k-1$
, with
![]() $\alpha_0=1$
and
$\alpha_0=1$
and
![]() $\alpha_t \in (0,1)$
for
$\alpha_t \in (0,1)$
for
![]() $t=1,\ldots, k-1$
.
$t=1,\ldots, k-1$
.
Case
![]() $\lvert\delta\rvert \to\pm \infty$
: Using forward substitution, we have that for
$\lvert\delta\rvert \to\pm \infty$
: Using forward substitution, we have that for
![]() $\delta \to \infty$
the solution of (20) is
$\delta \to \infty$
the solution of (20) is
 \begin{equation} \alpha_{t}=c^t \,\max_{i=1,\ldots, k}(d_{t-i} \,\alpha_{i-1}),\qquad d_{t-i}=\max \prod_{n=1}^k \gamma_{k+1-n}^{j_n}, \qquad t\geq k, \end{equation}
\begin{equation} \alpha_{t}=c^t \,\max_{i=1,\ldots, k}(d_{t-i} \,\alpha_{i-1}),\qquad d_{t-i}=\max \prod_{n=1}^k \gamma_{k+1-n}^{j_n}, \qquad t\geq k, \end{equation}
where the maximum for
![]() $d_{t-i}$
in (26) is taken over
$d_{t-i}$
in (26) is taken over
![]() $0\leq j_1\leq\ldots \leq j_k\leq t-i$
such that
$0\leq j_1\leq\ldots \leq j_k\leq t-i$
such that
![]() $\sum_{m=1}^{t-i} m\,j_m = t-i$
. The case
$\sum_{m=1}^{t-i} m\,j_m = t-i$
. The case
![]() $\delta \to -\infty$
is obtained by replacing the maximum operator in (26) by the minimum operator.
$\delta \to -\infty$
is obtained by replacing the maximum operator in (26) by the minimum operator.
5. Results for kernels based on important copula classes
5.1. Strategy for finding norming functionals
Our results in Section 3 provide powerful results for stationary kth-order Markov processes which derive the behaviour of hidden tail chains over all lags, given the appropriate norming functions
![]() $a_t, b_t$
, for lags
$a_t, b_t$
, for lags
![]() $t=1,\ldots, k-1$
, and the norming functionals a and b after an extreme event at time
$t=1,\ldots, k-1$
, and the norming functionals a and b after an extreme event at time
![]() $t=0$
. However, these results do not explain how to derive these quantities. Here we discuss general strategies for how to find these norming functions, with Section 5.3 providing a step-by-step illustration of how these strategies are implemented.
$t=0$
. However, these results do not explain how to derive these quantities. Here we discuss general strategies for how to find these norming functions, with Section 5.3 providing a step-by-step illustration of how these strategies are implemented.
The methods for finding
![]() $a_t, b_t$
for
$a_t, b_t$
for
![]() $t=1, \ldots ,k-1$
are well established; specifically, these can be obtained from Theorem 1 of [Reference Heffernan and Tawn9]. So the novelty here is in the derivation of a and b, which was not required in [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. Here we explain the general strategy for the case
$t=1, \ldots ,k-1$
are well established; specifically, these can be obtained from Theorem 1 of [Reference Heffernan and Tawn9]. So the novelty here is in the derivation of a and b, which was not required in [Reference Papastathopoulos, Strokorb, Tawn and Butler20]. Here we explain the general strategy for the case
![]() $a\neq 0$
and note that the case
$a\neq 0$
and note that the case
![]() $a=0$
and
$a=0$
and
![]() $b \neq 1$
is handled in a similar manner. Assuming that the conditional distribution of
$b \neq 1$
is handled in a similar manner. Assuming that the conditional distribution of
![]() $X_k\mid {\boldsymbol{X}}_{0\,:\,k-1}$
admits a Lebesgue density almost everywhere, a similar argument as in the proof of Theorem 1 in [Reference Heffernan and Tawn9] guarantees that the functionals a and b can be identified, up to type, by finding the functional forms of a and b, which satisfy the following two asymptotic properties: for all
$X_k\mid {\boldsymbol{X}}_{0\,:\,k-1}$
admits a Lebesgue density almost everywhere, a similar argument as in the proof of Theorem 1 in [Reference Heffernan and Tawn9] guarantees that the functionals a and b can be identified, up to type, by finding the functional forms of a and b, which satisfy the following two asymptotic properties: for all
![]() ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
,
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
,
and
where
![]() ${\boldsymbol{A}}_t({{v}},{\boldsymbol{z}})$
is defined by (7) with
${\boldsymbol{A}}_t({{v}},{\boldsymbol{z}})$
is defined by (7) with
![]() ${\boldsymbol{a}}_{t-k\,:\,t-1}$
and
${\boldsymbol{a}}_{t-k\,:\,t-1}$
and
![]() ${\boldsymbol{b}}_{t-k\,:\,t-1}$
as in Assumption 3. The expression (28) can be cumbersome to use in practice, so we resort to asymptotic inversion in order to identify b. In particular, to find a representative form for b, we make an informed choice based on the leading-order terms in an asymptotic expansion, as
${\boldsymbol{b}}_{t-k\,:\,t-1}$
as in Assumption 3. The expression (28) can be cumbersome to use in practice, so we resort to asymptotic inversion in order to identify b. In particular, to find a representative form for b, we make an informed choice based on the leading-order terms in an asymptotic expansion, as
![]() $v\rightarrow \infty$
, of the conditional distribution in (27) to obtain
$v\rightarrow \infty$
, of the conditional distribution in (27) to obtain
for all
![]() $y\in{{{\mathbb{R}}}}$
and
$y\in{{{\mathbb{R}}}}$
and
![]() ${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
, where
${\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
, where
![]() $K_A$
is a non-degenerate distribution on
$K_A$
is a non-degenerate distribution on
![]() ${{{\mathbb{R}}}}$
.
${{{\mathbb{R}}}}$
.
5.2. Examples of copula families and transition probability kernels
To illustrate the results in Theorems 1 and 2, we study the extremal behaviour of kth-order stationary Markov chains with unit-exponential margins, with transition probability kernels derived from the copula of
![]() $k+1$
consecutive values given in Section 5.3. Here we define the classes of copula families, and the associated transition probability kernels, that we use in Section 5.3 to derive the hidden tail chain behaviour. We have selected these copula families so we have families which give full pairwise asymptotic dependence, full pairwise asymptotic independence, and cases in between these; see Section 1 for the definition of these extremal process types. We can achieve all of these different properties from studying Gaussian, max-stable, and inverted max-stable copula families. The theory which motivates these copulas does not matter here; we simply view them as a range of interesting and well-known copula families whose extremes we study in a Markov setting.
$k+1$
consecutive values given in Section 5.3. Here we define the classes of copula families, and the associated transition probability kernels, that we use in Section 5.3 to derive the hidden tail chain behaviour. We have selected these copula families so we have families which give full pairwise asymptotic dependence, full pairwise asymptotic independence, and cases in between these; see Section 1 for the definition of these extremal process types. We can achieve all of these different properties from studying Gaussian, max-stable, and inverted max-stable copula families. The theory which motivates these copulas does not matter here; we simply view them as a range of interesting and well-known copula families whose extremes we study in a Markov setting.
First we present the link between a general
![]() $(k+1)$
-dimensional copula C and its associated transition probability kernel
$(k+1)$
-dimensional copula C and its associated transition probability kernel
![]() $\pi$
when working with a kth-order stationary Markov process with exponential margins. Let F denote the joint distribution function of a random vector
$\pi$
when working with a kth-order stationary Markov process with exponential margins. Let F denote the joint distribution function of a random vector
![]() ${\boldsymbol{X}}=(X_0,\ldots,X_{k})$
, assumed to be absolutely continuous with respect to Lebesgue measure with unit-exponential margins, that is,
${\boldsymbol{X}}=(X_0,\ldots,X_{k})$
, assumed to be absolutely continuous with respect to Lebesgue measure with unit-exponential margins, that is,
![]() $F_i(x)=F_E(x)=(1-\exp({-}x))_+$
,
$F_i(x)=F_E(x)=(1-\exp({-}x))_+$
,
![]() $i=0,\ldots,k$
. Writing
$i=0,\ldots,k$
. Writing
![]() $C\,:\,[0,1]^{k+1}\to [0,1]$
for the copula of
$C\,:\,[0,1]^{k+1}\to [0,1]$
for the copula of
![]() ${\boldsymbol{X}}$
, that is,
${\boldsymbol{X}}$
, that is,
![]() $C({\boldsymbol{u}})=F\big(F_E^\leftarrow(u_0),\ldots,F^\leftarrow_E(u_k)\big)$
, where
$C({\boldsymbol{u}})=F\big(F_E^\leftarrow(u_0),\ldots,F^\leftarrow_E(u_k)\big)$
, where
![]() ${\boldsymbol{u}}=(u_0,\ldots,u_k) \in [0,1]^{k+1}$
, we define the Markov kernel
${\boldsymbol{u}}=(u_0,\ldots,u_k) \in [0,1]^{k+1}$
, we define the Markov kernel
![]() $\pi_E\,:\, {{\mathscr{B}}}({{{\mathbb{R}}}}^k)\to [0,1]$
of the stationary process by
$\pi_E\,:\, {{\mathscr{B}}}({{{\mathbb{R}}}}^k)\to [0,1]$
of the stationary process by
with
![]() ${\boldsymbol{u}}_{0\,:\,k}=\{1-\exp({-}{\boldsymbol{x}}_{0\,:\,k})\}_+$
. Assuming the copula function satisfies appropriate conditions that ensure stationarity [Reference Joe12], the initial distribution
${\boldsymbol{u}}_{0\,:\,k}=\{1-\exp({-}{\boldsymbol{x}}_{0\,:\,k})\}_+$
. Assuming the copula function satisfies appropriate conditions that ensure stationarity [Reference Joe12], the initial distribution
![]() $F({\boldsymbol{x}}_{0\,:\,k-1},\infty)$
is the k-dimensional invariant distribution of a Markov process with unit-exponential margins and kernel
$F({\boldsymbol{x}}_{0\,:\,k-1},\infty)$
is the k-dimensional invariant distribution of a Markov process with unit-exponential margins and kernel
![]() $\pi_E$
.
$\pi_E$
.
Gaussian copula: Consider a stationary Gaussian autoregressive process with positive dependence transformed componentwise to have exponential marginal distributions. Let
![]() $\boldsymbol{\Sigma} \in {{{\mathbb{R}}}}^{(k+1) \times (k+1)}$
be a
$\boldsymbol{\Sigma} \in {{{\mathbb{R}}}}^{(k+1) \times (k+1)}$
be a
![]() $(k+1)$
-dimensional Toeplitz correlation matrix, that is,
$(k+1)$
-dimensional Toeplitz correlation matrix, that is,
![]() $\boldsymbol{\Sigma} = (\rho_{\lvert i-j \rvert})_{1 \leq i,j \leq k+1}$
with
$\boldsymbol{\Sigma} = (\rho_{\lvert i-j \rvert})_{1 \leq i,j \leq k+1}$
with
![]() $\rho_0=1$
,
$\rho_0=1$
,
![]() $\rho_i > 0$
, for
$\rho_i > 0$
, for
![]() $i=1,\ldots,k$
, which is assumed to be positive definite, and let
$i=1,\ldots,k$
, which is assumed to be positive definite, and let
![]() ${\boldsymbol{Q}}=\boldsymbol{\Sigma}^{-1} = (q_{i-1,j-1})_{1\leq i,j \leq k+1}$
. The distribution function of the standard
${\boldsymbol{Q}}=\boldsymbol{\Sigma}^{-1} = (q_{i-1,j-1})_{1\leq i,j \leq k+1}$
. The distribution function of the standard
![]() $(k+1)$
-dimensional Gaussian with mean
$(k+1)$
-dimensional Gaussian with mean
![]() ${\textbf{0}}_{k+1}$
and positive definite variance–covariance matrix
${\textbf{0}}_{k+1}$
and positive definite variance–covariance matrix
![]() $\boldsymbol{\Sigma}$
, in exponential margins, is
$\boldsymbol{\Sigma}$
, in exponential margins, is
 \begin{align*} F({\boldsymbol{x}}_{0\,:\,k})= \int\limits_{-\infty}^{\Phi^{\leftarrow}\{1-\exp({-} x_{k})\}}\cdots \int\limits_{-\infty}^{\Phi^{\leftarrow}\{1-\exp({-} x_{0})\}} \frac{\{\text{det}( {\boldsymbol{Q}})\}^{1/2}}{(2\pi)^{(k+1)/2}}\, e^{- {\boldsymbol{s}}^{\top}{\boldsymbol{Q}} {\boldsymbol{s}}/2}\,\mathrm{d}{\boldsymbol{s}}, \end{align*}
\begin{align*} F({\boldsymbol{x}}_{0\,:\,k})= \int\limits_{-\infty}^{\Phi^{\leftarrow}\{1-\exp({-} x_{k})\}}\cdots \int\limits_{-\infty}^{\Phi^{\leftarrow}\{1-\exp({-} x_{0})\}} \frac{\{\text{det}( {\boldsymbol{Q}})\}^{1/2}}{(2\pi)^{(k+1)/2}}\, e^{- {\boldsymbol{s}}^{\top}{\boldsymbol{Q}} {\boldsymbol{s}}/2}\,\mathrm{d}{\boldsymbol{s}}, \end{align*}
for
![]() ${\boldsymbol{x}}_{0\,:\,k} \in {{{\mathbb{R}}}}_+^{k+1}$
and
${\boldsymbol{x}}_{0\,:\,k} \in {{{\mathbb{R}}}}_+^{k+1}$
and
![]() ${\boldsymbol{s}}=(s_0,\ldots, s_{k})^\top$
, where
${\boldsymbol{s}}=(s_0,\ldots, s_{k})^\top$
, where
![]() $\Phi^{\leftarrow}\,:\,[0,1]\to {{{\mathbb{R}}}}$
denotes the quantile function of the standard normal distribution function
$\Phi^{\leftarrow}\,:\,[0,1]\to {{{\mathbb{R}}}}$
denotes the quantile function of the standard normal distribution function
![]() $\Phi(\cdot)$
. This choice of correlation function ensures stationarity of the resulting Markov chain, and the joint distribution gives the transition probability kernel
$\Phi(\cdot)$
. This choice of correlation function ensures stationarity of the resulting Markov chain, and the joint distribution gives the transition probability kernel
for
![]() $({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
, where the kernel
$({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
, where the kernel
![]() $\pi_G$
is the full conditional distribution function of the multivariate normal, given by
$\pi_G$
is the full conditional distribution function of the multivariate normal, given by
 \begin{align*} \pi_G({\boldsymbol{x}}_{0\,:\,k-1}, x_k) = \Phi\Bigg[q_{kk}^{1/2}\Bigg\{x_k- \sum_{t=0}^{k-1}\bigg({-}\frac{q_{tk}}{q_{kk}}\bigg)\,x_t \Bigg\}\Bigg], \end{align*}
\begin{align*} \pi_G({\boldsymbol{x}}_{0\,:\,k-1}, x_k) = \Phi\Bigg[q_{kk}^{1/2}\Bigg\{x_k- \sum_{t=0}^{k-1}\bigg({-}\frac{q_{tk}}{q_{kk}}\bigg)\,x_t \Bigg\}\Bigg], \end{align*}
where
![]() $\Phi$
is the standard normal distribution function. The condition
$\Phi$
is the standard normal distribution function. The condition
![]() $\rho_i > 0$
, for
$\rho_i > 0$
, for
![]() $i=1,\ldots, k$
, appears restrictive but is made to simplify the presentation. If we worked with standard Laplace marginals, instead of exponential marginals, as say in [Reference Keef, Papastathopoulos and Tawn13], the presentation would be equally simple for any values
$i=1,\ldots, k$
, appears restrictive but is made to simplify the presentation. If we worked with standard Laplace marginals, instead of exponential marginals, as say in [Reference Keef, Papastathopoulos and Tawn13], the presentation would be equally simple for any values
![]() $\lvert \rho_i \rvert > 0$
,
$\lvert \rho_i \rvert > 0$
,
![]() $i=1,\ldots,k$
, of the correlation matrix
$i=1,\ldots,k$
, of the correlation matrix
![]() $\boldsymbol{\Sigma}$
.
$\boldsymbol{\Sigma}$
.
Max-stable copula: A class of transition probability kernels for asymptotically dependent Markov processes is obtained from the class of multivariate extreme-value distributions [Reference Resnick25]. The
![]() $(k+1)$
-dimensional distribution function of the multivariate extreme- value distribution with exponential margins is given by
$(k+1)$
-dimensional distribution function of the multivariate extreme- value distribution with exponential margins is given by
for
![]() ${\boldsymbol{x}}_{0\,:\,k} \in {{{\mathbb{R}}}}^{k+1}_+$
, with
${\boldsymbol{x}}_{0\,:\,k} \in {{{\mathbb{R}}}}^{k+1}_+$
, with
![]() $V\,:\,{{{\mathbb{R}}}}_+^{k+1}\to {{{\mathbb{R}}}}_+$
a
$V\,:\,{{{\mathbb{R}}}}_+^{k+1}\to {{{\mathbb{R}}}}_+$
a
![]() $-1$
-homogeneous function, known as the exponent function, given by
$-1$
-homogeneous function, known as the exponent function, given by
where H is termed the spectral measure on
![]() ${{\Delta}}^k$
that has total mass
${{\Delta}}^k$
that has total mass
![]() $k+1$
and satisfies the moment constraints
$k+1$
and satisfies the moment constraints
![]() $\int_{{{\Delta}}^{k}} \omega_i H(\mathrm{d}\boldsymbol{\omega}) = 1$
, for
$\int_{{{\Delta}}^{k}} \omega_i H(\mathrm{d}\boldsymbol{\omega}) = 1$
, for
![]() $i = 0,\ldots,k$
. Throughout this section, we assume that V has continuous mixed partial derivatives of all orders, which ensures that a density for F exists [Reference Coles and Tawn4]. For any
$i = 0,\ldots,k$
. Throughout this section, we assume that V has continuous mixed partial derivatives of all orders, which ensures that a density for F exists [Reference Coles and Tawn4]. For any
![]() $J \subseteq [k]$
, we write
$J \subseteq [k]$
, we write
![]() $V_J$
to denote the higher-order partial derivative
$V_J$
to denote the higher-order partial derivative
![]() $\partial^{\lvert J \lvert} V({\boldsymbol{x}}_{0\,:\,k})/\prod_{j \in J}\partial x_j$
and
$\partial^{\lvert J \lvert} V({\boldsymbol{x}}_{0\,:\,k})/\prod_{j \in J}\partial x_j$
and
![]() $\Pi_{m}$
for the set of partitions of
$\Pi_{m}$
for the set of partitions of
![]() $[m]\,:\!=\,$
$[m]\,:\!=\,$
![]() $\{0,1,\ldots,m\}$
, where
$\{0,1,\ldots,m\}$
, where
![]() $m=0,\ldots,k$
. Furthermore, for a vector
$m=0,\ldots,k$
. Furthermore, for a vector
![]() ${\boldsymbol{z}} = ({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
, we write
${\boldsymbol{z}} = ({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
, we write
![]() $V({\boldsymbol{z}})= V({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
. For
$V({\boldsymbol{z}})= V({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
. For
![]() $m = 0,\ldots, k-1$
we define
$m = 0,\ldots, k-1$
we define
![]() $V({\boldsymbol{x}}_{0\,:\,m}, \,\infty \cdot {\textbf{1}}_{k-m})\,:\!=\,\lim_{{\boldsymbol{x}}_{m+1\,:k} \to \infty \cdot {\textbf{1}}_{k-m}}V({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
, and for
$V({\boldsymbol{x}}_{0\,:\,m}, \,\infty \cdot {\textbf{1}}_{k-m})\,:\!=\,\lim_{{\boldsymbol{x}}_{m+1\,:k} \to \infty \cdot {\textbf{1}}_{k-m}}V({\boldsymbol{x}}_{0\,:\,m}, {\boldsymbol{x}}_{m+1\,:\,k})$
, and for
![]() $J\subseteq [m]$
, we define
$J\subseteq [m]$
, we define
![]() $V_{J}({\boldsymbol{x}}_{0\,:\,m}, \infty\cdot{\textbf{1}}_{k-m})\,:\!=\,\partial^{\lvert J \rvert}\,V({\boldsymbol{x}}_{0\,:\,m}, \infty \cdot {\textbf{1}}_{k-m})/\prod_{j\in J}\partial x_j$
. Stationarity is achieved by requiring that for any set
$V_{J}({\boldsymbol{x}}_{0\,:\,m}, \infty\cdot{\textbf{1}}_{k-m})\,:\!=\,\partial^{\lvert J \rvert}\,V({\boldsymbol{x}}_{0\,:\,m}, \infty \cdot {\textbf{1}}_{k-m})/\prod_{j\in J}\partial x_j$
. Stationarity is achieved by requiring that for any set
![]() $A\subset {{\mathbb{Z}}}$
, the distributions of
$A\subset {{\mathbb{Z}}}$
, the distributions of
![]() $\{X_i\,:\,i\in A\}$
and
$\{X_i\,:\,i\in A\}$
and
![]() $\{X_i\,:\,i\in B\}$
are identical when the set B is a translation of the set A, i.e., when there exists a unique
$\{X_i\,:\,i\in B\}$
are identical when the set B is a translation of the set A, i.e., when there exists a unique
![]() $\omega \in {{\mathbb{Z}}}$
such that
$\omega \in {{\mathbb{Z}}}$
such that
![]() $B = \{x + \omega\,:\, x\in A\}$
. Given the Markov property, stationarity is ensured if V satisfies the property that
$B = \{x + \omega\,:\, x\in A\}$
. Given the Markov property, stationarity is ensured if V satisfies the property that
for any set
![]() $A\subseteq [k]$
, where B is a translation of the set A, with
$A\subseteq [k]$
, where B is a translation of the set A, with
![]() $B\subseteq [k]$
. The transition probability kernel induced by the multivariate extreme value copula, in exponential margins, is
$B\subseteq [k]$
. The transition probability kernel induced by the multivariate extreme value copula, in exponential margins, is
 \begin{eqnarray} \pi_E({\boldsymbol{x}}_{0\,:\,k-1}, x_k) &=& \frac{\big[ \sum_{p \in \Pi_{k-1} }({-}1)^{\lvert p \lvert} \prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k})\big]} {\big[\sum_{p \in \Pi_{k-1}}({-}1)^{\lvert p\lvert} \prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k-1}, \infty)\big]} \nonumber \\\nonumber\\ && \times \exp\{V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) - V({\boldsymbol{y}}_{0\,:\,k})\}, \end{eqnarray}
\begin{eqnarray} \pi_E({\boldsymbol{x}}_{0\,:\,k-1}, x_k) &=& \frac{\big[ \sum_{p \in \Pi_{k-1} }({-}1)^{\lvert p \lvert} \prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k})\big]} {\big[\sum_{p \in \Pi_{k-1}}({-}1)^{\lvert p\lvert} \prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k-1}, \infty)\big]} \nonumber \\\nonumber\\ && \times \exp\{V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) - V({\boldsymbol{y}}_{0\,:\,k})\}, \end{eqnarray}
where
![]() $({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
and with
$({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
and with
![]() ${\boldsymbol{y}}_{0\,:\,k}$
as defined in (30).
${\boldsymbol{y}}_{0\,:\,k}$
as defined in (30).
Inverted max-stable: The final class of transition kernels is based on the class of inverted max-stable distributions [Reference Ledford and Tawn16, Reference Papastathopoulos and Tawn21]. The specification of this distribution is most elegantly expressed in terms of its
![]() $(k+1)$
-dimensional survivor function. In exponential margins, this is expressed as
$(k+1)$
-dimensional survivor function. In exponential margins, this is expressed as
where V denotes an exponent function as defined by (31). To ensure stationarity, V is assumed to satisfy the conditions (32). This distribution gives the transition probability kernel
where
![]() $({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
and
$({\boldsymbol{x}}_{0\,:\,k-1}, x_k) \in {{{\mathbb{R}}}}^{k} \times {{{\mathbb{R}}}}$
and
![]() $\pi_E$
is as given by (33).
$\pi_E$
is as given by (33).
5.3. Examples of norming function and hidden tail chains
For a range of examples of kth-order Markov processes, we illustrate how the theory we have developed is applicable, and we derive the forms of the required norming functions and identify the properties of the hidden tail chains. The examples include the full pairwise asymptotically dependent max-stable distribution family, and specifically two subclasses known as the logistic [Reference Beirlant, Goegebeur, Segers and Teugels2] and Hüsler–Reiss [Reference Engelke, Malinowski, Kabluchko and Schlather7, Reference Huser and Davison10] dependence structures. They also include two classes of full pairwise asymptotically independent distributions, the Gaussian copula and the inverted max-stable distribution with logistic dependence structure. We also illustrate the sub-asymptotic behaviour of these hidden tail chains in Figure 1, through simulation of the Markov process after a large event. Our proofs that the required the weak convergence of each transition probability kernel satisfies the assumptions of Section 2 are presented in Appendices A.5–A.9, where we implement step by step the strategy we outlined in Section 5.1 to find the required norming functions.

Figure 1. Properties for each hidden tail chain for Examples 1–3 with
![]() $k=5$
. Presented for each chain are pointwise 2.5% and 97.5% quantiles of the sampling distribution (shaded region), mean of the sampling distribution (dashed line), and one realization from the (hidden) tail chain (solid line). The copula of
$k=5$
. Presented for each chain are pointwise 2.5% and 97.5% quantiles of the sampling distribution (shaded region), mean of the sampling distribution (dashed line), and one realization from the (hidden) tail chain (solid line). The copula of
![]() ${\boldsymbol{X}}_{0\,:\,k}$
used to derive the (hidden) tail chain comes from (a) the standard multivariate Gaussian copula with Toeplitz positive definite covariance matrix
${\boldsymbol{X}}_{0\,:\,k}$
used to derive the (hidden) tail chain comes from (a) the standard multivariate Gaussian copula with Toeplitz positive definite covariance matrix
![]() $\Sigma$
generated by the vector
$\Sigma$
generated by the vector
![]() $(1, 0.70, 0.57, 0.47, 0.39, 0.33)$
, and (b) the inverted logistic with
$(1, 0.70, 0.57, 0.47, 0.39, 0.33)$
, and (b) the inverted logistic with
![]() $\alpha=\log({\textbf{1}}_{k+1}^\top\,\Sigma^{-1}\,{\textbf{1}}_{k+1})/\log k=0.27$
(here the value of the function
$\alpha=\log({\textbf{1}}_{k+1}^\top\,\Sigma^{-1}\,{\textbf{1}}_{k+1})/\log k=0.27$
(here the value of the function
![]() $\text{mod}_k(t)$
is also highlighted on the mean function of the time series with numbers ranging from 0 to 4 for all t), (c) the logistic copula with
$\text{mod}_k(t)$
is also highlighted on the mean function of the time series with numbers ranging from 0 to 4 for all t), (c) the logistic copula with
![]() $\alpha=0.32$
, and (d) the Hüsler–Reiss copula with Toeplitz positive definite covariance matrix generated by the vector
$\alpha=0.32$
, and (d) the Hüsler–Reiss copula with Toeplitz positive definite covariance matrix generated by the vector
![]() $(1, 0.9, 0.7, 0.5, 0.3, 0.1)$
. The parameters for all copulas are chosen so that the coefficient of residual tail dependence
$(1, 0.9, 0.7, 0.5, 0.3, 0.1)$
. The parameters for all copulas are chosen so that the coefficient of residual tail dependence
![]() $\eta$
[Reference Ledford and Tawn16] and the extremal coefficient
$\eta$
[Reference Ledford and Tawn16] and the extremal coefficient
![]() $\theta$
[Reference Beirlant, Goegebeur, Segers and Teugels2] are equal for the copulas in panels (a) and (b), and for those in panels (c) and (d), respectively.
$\theta$
[Reference Beirlant, Goegebeur, Segers and Teugels2] are equal for the copulas in panels (a) and (b), and for those in panels (c) and (d), respectively.
We also consider an example of a Markov process not covered by the theory we have developed, but for which we can directly derive the norming functions and the hidden tail chain behaviour. This is a second-order stationary Markov chain with a transition probability kernel using a max-stable distribution which permits the possibility of sudden switches from extreme to non-extreme states and vice versa. In this setting, a novel form of normalization of the transition probability kernel is required, which, together with the associated hidden tail chain, carries information about the mechanism that governs the sudden transitions. In Figure 2 we illustrate that the sub-asymptotic properties of this process are captured by our asymptotic results. Although the development of general theory for this type of process is beyond the scope of this paper, this example serves to motivate future extensions of our theory.

Figure 2. (a) Time series plot showing a single realization from the second-order Markov chain with asymmetric logistic dependence (46) initialized from the distribution of
![]() $X_0\mid X_0 > 9$
. For this realization, there are three change-points
$X_0\mid X_0 > 9$
. For this realization, there are three change-points
![]() $T_1^X$
,
$T_1^X$
,
![]() $T_2^X$
, and
$T_2^X$
, and
![]() $T_3^X$
, which are highlighted with crosses. (b) Scatter-plot of states
$T_3^X$
, which are highlighted with crosses. (b) Scatter-plot of states
![]() $\{(X_{t-1},X_{t})\,:\, X_{t-1} > 9\}$
drawn from
$\{(X_{t-1},X_{t})\,:\, X_{t-1} > 9\}$
drawn from
![]() $10^3$
realizations of the Markov chain initialized from the distribution of
$10^3$
realizations of the Markov chain initialized from the distribution of
![]() $X_0\mid X_0>9$
. Points for which
$X_0\mid X_0>9$
. Points for which
![]() $X_{t-2}<9$
and
$X_{t-2}<9$
and
![]() $X_{t-2}\geq 9$
are highlighted with grey crosses and black circles, respectively. (c) Scatter-plot of consecutive states
$X_{t-2}\geq 9$
are highlighted with grey crosses and black circles, respectively. (c) Scatter-plot of consecutive states
![]() $(X_{t-2},X_{t})$
. Points for which
$(X_{t-2},X_{t})$
. Points for which
![]() $X_{t-1}<9$
and
$X_{t-1}<9$
and
![]() $X_{t-1}\geq 9$
are highlighted with grey crosses and black circles, respectively. (d) Scatter-plot of states
$X_{t-1}\geq 9$
are highlighted with grey crosses and black circles, respectively. (d) Scatter-plot of states
![]() $\{(\max(X_{t-2},X_{t-1}), X_t)\,:\, \max(X_{t-2}, X_{t-1}) > 9\}$
and line
$\{(\max(X_{t-2},X_{t-1}), X_t)\,:\, \max(X_{t-2}, X_{t-1}) > 9\}$
and line
![]() $X_t = c\,\max(X_{t-2},X_{t-1})$
with
$X_t = c\,\max(X_{t-2},X_{t-1})$
with
![]() $c=\frac{1}{2}$
superposed. (e) Histogram of termination time
$c=\frac{1}{2}$
superposed. (e) Histogram of termination time
![]() $T^B$
obtained from
$T^B$
obtained from
![]() $10^4$
realizations from the hidden tail chain. The Monte Carlo estimate of the mean of the distribution is
$10^4$
realizations from the hidden tail chain. The Monte Carlo estimate of the mean of the distribution is
![]() $8.42$
and shown with a dashed vertical line. (f) Pointwise 2.5% and 97.5% quantiles of the sampling distribution (shaded region), mean of the sampling distribution (dashed line), and one realization from the hidden tail chain (solid line), conditioned on
$8.42$
and shown with a dashed vertical line. (f) Pointwise 2.5% and 97.5% quantiles of the sampling distribution (shaded region), mean of the sampling distribution (dashed line), and one realization from the hidden tail chain (solid line), conditioned on
![]() $T^B=8$
. The value of the latent Bernoulli process
$T^B=8$
. The value of the latent Bernoulli process
![]() $B_t$
is highlighted with a cross when
$B_t$
is highlighted with a cross when
![]() $B_t=0$
and with a circle when
$B_t=0$
and with a circle when
![]() $B_t=1$
. For all plots presented,
$B_t=1$
. For all plots presented,
![]() $\theta_{0}=\theta_{1}=\theta_{2}=\theta_{01}=\theta_{02} = 0.3$
,
$\theta_{0}=\theta_{1}=\theta_{2}=\theta_{01}=\theta_{02} = 0.3$
,
![]() $\theta_{012}=0.1$
, and
$\theta_{012}=0.1$
, and
![]() $\nu_{01}=\nu_{02}=\nu_{012}=0.5$
.
$\nu_{01}=\nu_{02}=\nu_{012}=0.5$
.
Example 1. (Stationary Gaussian autoregressive process—positive dependence.) For this copula, under the notation and conditions described in Section 5.2, [Reference Heffernan and Tawn9, Section 8.6] showed that Assumption 2 holds with norming functions
![]() $a_i(v)=\rho_i^2 v$
,
$a_i(v)=\rho_i^2 v$
,
![]() $b_i(v)=v^{1/2}$
, that is,
$b_i(v)=v^{1/2}$
, that is,
![]() $\alpha_i = \rho_i^2$
and
$\alpha_i = \rho_i^2$
and
![]() $\beta_i=1/2$
, for
$\beta_i=1/2$
, for
![]() $i=1,\ldots,k-1$
and initial limiting distribution
$i=1,\ldots,k-1$
and initial limiting distribution
![]() $G({\boldsymbol{z}}_{1\,:\,k-1})=\Phi_k({\boldsymbol{z}}_{1\,:\,k-1}; \Sigma_0)$
, where
$G({\boldsymbol{z}}_{1\,:\,k-1})=\Phi_k({\boldsymbol{z}}_{1\,:\,k-1}; \Sigma_0)$
, where
![]() ${\boldsymbol{z}}_{1\,:\,k-1} \in {{{\mathbb{R}}}}^{k-1}$
and
${\boldsymbol{z}}_{1\,:\,k-1} \in {{{\mathbb{R}}}}^{k-1}$
and
![]() $\Phi_k(\cdot;\boldsymbol{\Sigma}_0)$
denotes the cumulative distribution function of the k-dimensional multivariate normal distribution with a zero mean vector and covariance matrix
$\Phi_k(\cdot;\boldsymbol{\Sigma}_0)$
denotes the cumulative distribution function of the k-dimensional multivariate normal distribution with a zero mean vector and covariance matrix
![]() $\Sigma_0=(2 \rho_{i}\,\rho_{j}(\rho_{\lvert j-i\lvert}- \rho_i\,\rho_j))_{1\leq i,j\leq k-1}$
. Appendix A.5 shows that Assumption 3 holds with norming functionals
$\Sigma_0=(2 \rho_{i}\,\rho_{j}(\rho_{\lvert j-i\lvert}- \rho_i\,\rho_j))_{1\leq i,j\leq k-1}$
. Appendix A.5 shows that Assumption 3 holds with norming functionals
 \begin{eqnarray} a({\boldsymbol{u}})=\Bigg(\sum_{i=1}^{k} \phi_i \, u_i^{1/2}\Bigg)^2, &\qquad b({\boldsymbol{u}})=a({\boldsymbol{u}})^{1/2}, & \qquad {\boldsymbol{u}}=(u_1,\ldots,u_k)\in {{{\mathbb{R}}}}_+^k, \end{eqnarray}
\begin{eqnarray} a({\boldsymbol{u}})=\Bigg(\sum_{i=1}^{k} \phi_i \, u_i^{1/2}\Bigg)^2, &\qquad b({\boldsymbol{u}})=a({\boldsymbol{u}})^{1/2}, & \qquad {\boldsymbol{u}}=(u_1,\ldots,u_k)\in {{{\mathbb{R}}}}_+^k, \end{eqnarray}
where
![]() $\phi_{i} = -q_{k-i,k}/q_{kk}$
,
$\phi_{i} = -q_{k-i,k}/q_{kk}$
,
![]() $i=1,\ldots, k$
, denote the first k partial autocorrelation coefficients of the stationary Gaussian process (on Gaussian margins), and the transition probability kernel of the renormalized Markov chain converges weakly to the distribution
$i=1,\ldots, k$
, denote the first k partial autocorrelation coefficients of the stationary Gaussian process (on Gaussian margins), and the transition probability kernel of the renormalized Markov chain converges weakly to the distribution
Corollary 2 asserts that a suitable location normalization after
![]() $t\geq k$
steps has
$t\geq k$
steps has
![]() $\alpha_t=a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) = \rho_t^2$
and
$\alpha_t=a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) = \rho_t^2$
and
![]() $\beta_t={1/2}$
. This equivalence arises from the a function in (36) and the Yule–Walker equations for stationary Gaussian autoregressive processes, that is,
$\beta_t={1/2}$
. This equivalence arises from the a function in (36) and the Yule–Walker equations for stationary Gaussian autoregressive processes, that is,
![]() $\rho_t= \sum_{i=1}^k \phi_i \, \rho_{t-i}$
, for
$\rho_t= \sum_{i=1}^k \phi_i \, \rho_{t-i}$
, for
![]() $t\geq k$
. As all stationary Gaussian finite-order Markov chains have that
$t\geq k$
. As all stationary Gaussian finite-order Markov chains have that
![]() $\rho_t\rightarrow 0$
geometrically as
$\rho_t\rightarrow 0$
geometrically as
![]() $t\rightarrow \infty$
, it follows that
$t\rightarrow \infty$
, it follows that
![]() $\alpha_t$
does likewise.
$\alpha_t$
does likewise.
Now consider the hidden tail chain. The gradient vector of a is
 \begin{align*} \nabla a({\boldsymbol{u}})=\Bigg\{(\phi_j u_j)^{-1/2}\sum_{i=1}^k \phi_i u_i^{1/2} \,:\, j=1,\ldots,k\Bigg\}. \end{align*}
\begin{align*} \nabla a({\boldsymbol{u}})=\Bigg\{(\phi_j u_j)^{-1/2}\sum_{i=1}^k \phi_i u_i^{1/2} \,:\, j=1,\ldots,k\Bigg\}. \end{align*}
Thus, based on the Yule–Walker equations, we have
Also,
![]() $b(\boldsymbol{\alpha}_{t-k\,:\,t-1})= a(\boldsymbol{\alpha}_{t-k\,:\,t-1})^{1/2}=\rho_t$
. This leads to the scaled autoregressive hidden tail chain
$b(\boldsymbol{\alpha}_{t-k\,:\,t-1})= a(\boldsymbol{\alpha}_{t-k\,:\,t-1})^{1/2}=\rho_t$
. This leads to the scaled autoregressive hidden tail chain
 \begin{equation} {{Z}}_t = \rho_t \, \sum_{i=1}^k \frac{\phi_i}{\rho_{t-i}} \, {{Z}}_{t-i} + \rho_t \, \varepsilon_t, \qquad t \geq k, \end{equation}
\begin{equation} {{Z}}_t = \rho_t \, \sum_{i=1}^k \frac{\phi_i}{\rho_{t-i}} \, {{Z}}_{t-i} + \rho_t \, \varepsilon_t, \qquad t \geq k, \end{equation}
and
![]() $\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
$\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
![]() $K_A$
given by (37). The hidden tail chain is a non-stationary kth-order autoregressive Gaussian process with zero mean and autocovariance function
$K_A$
given by (37). The hidden tail chain is a non-stationary kth-order autoregressive Gaussian process with zero mean and autocovariance function
![]() $\text{cov}({{Z}}_{t-s}, {{Z}}_t) = (2 \rho_{t-s}\,\rho_{t}(\rho_{s}- \rho_{t-s}\,\rho_{t}))$
when
$\text{cov}({{Z}}_{t-s}, {{Z}}_t) = (2 \rho_{t-s}\,\rho_{t}(\rho_{s}- \rho_{t-s}\,\rho_{t}))$
when
![]() $t\neq s$
. The variance of the process satisfies
$t\neq s$
. The variance of the process satisfies
![]() $\text{var}({{Z}}_t)=\mathcal{O}(\rho_t^2)$
as
$\text{var}({{Z}}_t)=\mathcal{O}(\rho_t^2)$
as
![]() $t\to \infty$
; hence the hidden tail chain degenerates to 0 in the limit as
$t\to \infty$
; hence the hidden tail chain degenerates to 0 in the limit as
![]() $t\to \infty$
. This long-term degenerative behaviour is illustrated in panel (a) of Figure 1.
$t\to \infty$
. This long-term degenerative behaviour is illustrated in panel (a) of Figure 1.
Remark 5. The location functional a in (36) can be written in the form (22) with
![]() $c = \sum_{i=1}^k\phi_i$
and
$c = \sum_{i=1}^k\phi_i$
and
![]() $\gamma_i = \phi_i^{2/3}/\sum_j\phi_j^{2/3}$
for
$\gamma_i = \phi_i^{2/3}/\sum_j\phi_j^{2/3}$
for
![]() $i=1, \ldots ,k$
.
$i=1, \ldots ,k$
.
Example 2. (Inverted max-stable copula with logistic dependence.) Consider a stationary kth-order Markov chain with a
![]() $(k+1)$
-dimensional survivor function (34) and exponent function of logistic type given by
$(k+1)$
-dimensional survivor function (34) and exponent function of logistic type given by
where
![]() $\alpha \in (0,1)$
, which gives a stationary process as V is an exchangeable function. [Reference Heffernan and Tawn9, Section 8.5] showed that Assumption 4 holds with
$\alpha \in (0,1)$
, which gives a stationary process as V is an exchangeable function. [Reference Heffernan and Tawn9, Section 8.5] showed that Assumption 4 holds with
![]() $b_i(v)=v^{1-\alpha}$
, that is,
$b_i(v)=v^{1-\alpha}$
, that is,
![]() $\beta_i=1-\alpha$
for
$\beta_i=1-\alpha$
for
![]() $i=1\ldots, k-1$
, and limiting initial conditional distribution
$i=1\ldots, k-1$
, and limiting initial conditional distribution
![]() $G({\boldsymbol{z}})= \prod_{i=1}^{k-1}\big\{1-\exp\big({-}\alpha{{z}}_i^{1/\alpha}\big)\big\}$
,
$G({\boldsymbol{z}})= \prod_{i=1}^{k-1}\big\{1-\exp\big({-}\alpha{{z}}_i^{1/\alpha}\big)\big\}$
,
![]() ${\boldsymbol{z}} \in (0,\infty)^{k-1}$
. Appendix A.6 shows that Assumption 5 holds with normalizing functionals
${\boldsymbol{z}} \in (0,\infty)^{k-1}$
. Appendix A.6 shows that Assumption 5 holds with normalizing functionals
and the transition probability kernel of the renormalized Markov chain converges weakly to the distribution
as
![]() $u \to \infty$
. Corollary 3 asserts that a suitable normalization after
$u \to \infty$
. Corollary 3 asserts that a suitable normalization after
![]() $t\geq k$
steps is
$t\geq k$
steps is
![]() $a_t(v)=0$
,
$a_t(v)=0$
,
![]() $\log b_t(v)=({(1-\alpha)^{1 + \lfloor (t-1)/k\rfloor}}) \, \log v$
, which leads to the scaled random walk hidden tail chain
$\log b_t(v)=({(1-\alpha)^{1 + \lfloor (t-1)/k\rfloor}}) \, \log v$
, which leads to the scaled random walk hidden tail chain
 \begin{align*} {{Z}}_{t} = \begin{cases} \lVert ({{Z}}_{t-k}, {\textbf{0}}_{k-1})^{1/\alpha}\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t)=0$},\\[3pt] \lVert{\boldsymbol{Z}}_{t-k\,:\,t-1}^{1/\alpha}\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t)=1$},\\[3pt] \big\lVert\big({\boldsymbol{Z}}_{t-k\,:\,t-j}^{1/\alpha}, {\textbf{0}}_{j-1}\big)\big\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t) = j\in\{2,\ldots,k-1\}$}, \end{cases} \end{align*}
\begin{align*} {{Z}}_{t} = \begin{cases} \lVert ({{Z}}_{t-k}, {\textbf{0}}_{k-1})^{1/\alpha}\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t)=0$},\\[3pt] \lVert{\boldsymbol{Z}}_{t-k\,:\,t-1}^{1/\alpha}\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t)=1$},\\[3pt] \big\lVert\big({\boldsymbol{Z}}_{t-k\,:\,t-j}^{1/\alpha}, {\textbf{0}}_{j-1}\big)\big\rVert^{\alpha (1-\alpha)} \,\varepsilon_{t} & \text{when $\text{mod}_k(t) = j\in\{2,\ldots,k-1\}$}, \end{cases} \end{align*}
where
![]() $\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
$\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
![]() $K_B$
.
$K_B$
.
This hidden tail chain is a non-stationary process; specifically, after a logarithmic transformation, it is a non-stationary nonlinear kth-order autoregressive process. The first element of the process is
![]() ${{Z}}_0=1$
a.s., and the next
${{Z}}_0=1$
a.s., and the next
![]() $k-1$
elements of the process
$k-1$
elements of the process
![]() ${\boldsymbol{Z}}_{1\,:\,k-1}$
are i.i.d. positive random variables with distribution function
${\boldsymbol{Z}}_{1\,:\,k-1}$
are i.i.d. positive random variables with distribution function
![]() $K_B(x)$
,
$K_B(x)$
,
![]() $x > 0$
. Subsequent elements
$x > 0$
. Subsequent elements
![]() ${{Z}}_t$
, for
${{Z}}_t$
, for
![]() $t\geq k$
, have distributions that vary in both mean and variance. For b given by (40) and any
$t\geq k$
, have distributions that vary in both mean and variance. For b given by (40) and any
![]() ${\boldsymbol{x}}_{1:k} \in {{{\mathbb{R}}}}^k_+$
, we see that
${\boldsymbol{x}}_{1:k} \in {{{\mathbb{R}}}}^k_+$
, we see that
![]() $b({\boldsymbol{x}}_{1:k}) > b( {\boldsymbol{x}}_{2:k}, 0) > \cdots > b(x_k, {\textbf{0}}_{k-1})$
. This leads to an oscillating behaviour which is illustrated in panel (b) of Figure 1. In particular, both the mean and variance of the hidden tail chain can be seen to decrease in a segment of k consecutive time points
$b({\boldsymbol{x}}_{1:k}) > b( {\boldsymbol{x}}_{2:k}, 0) > \cdots > b(x_k, {\textbf{0}}_{k-1})$
. This leads to an oscillating behaviour which is illustrated in panel (b) of Figure 1. In particular, both the mean and variance of the hidden tail chain can be seen to decrease in a segment of k consecutive time points
![]() $(s, s+1, \ldots, s+k-1)$
for any
$(s, s+1, \ldots, s+k-1)$
for any
![]() $s > k$
such that
$s > k$
such that
![]() $\text{mod}_k(s) = 1$
.
$\text{mod}_k(s) = 1$
.
Example 3. (Multivariate extreme value copula—all mass on interior of simplex.) [Reference Heffernan and Tawn9, Section 8.4] showed that if the spectral measure H in (31) places no mass on the boundary of
![]() ${{\Delta}}^k$
, then Assumption 2 holds for the distribution (30) with norming functions
${{\Delta}}^k$
, then Assumption 2 holds for the distribution (30) with norming functions
![]() $a_i(v)=v$
,
$a_i(v)=v$
,
![]() $b_i(v)=1$
, i.e.
$b_i(v)=1$
, i.e.
![]() $\alpha_i=1$
,
$\alpha_i=1$
,
![]() $\beta_i=0$
, for
$\beta_i=0$
, for
![]() $i=1,\ldots,k-1$
, and limiting distribution
$i=1,\ldots,k-1$
, and limiting distribution
In this set-up we trivially have that the functional
![]() $b\equiv 1$
. For determining the functional a, Appendix A.7 shows that for any choice of a satisfying the condition (19), the limit integral (9) is
$b\equiv 1$
. For determining the functional a, Appendix A.7 shows that for any choice of a satisfying the condition (19), the limit integral (9) is
![]() $\int_{{{{\mathbb{R}}}}} f(x)K(dx; {\boldsymbol{z}}_{1\,:\,k-1})$
, with
$\int_{{{{\mathbb{R}}}}} f(x)K(dx; {\boldsymbol{z}}_{1\,:\,k-1})$
, with
![]() ${\boldsymbol{z}}_{1\,:\,k-1}\in{{{\mathbb{R}}}}^{k-1}$
, which is not in the form required by Assumption
${\boldsymbol{z}}_{1\,:\,k-1}\in{{{\mathbb{R}}}}^{k-1}$
, which is not in the form required by Assumption
![]() $A_2$
, as the K term is not independent of
$A_2$
, as the K term is not independent of
![]() ${\boldsymbol{z}}_{1\,:\,k-1}$
as is
${\boldsymbol{z}}_{1\,:\,k-1}$
as is
![]() $K_A$
in the statement of the assumption. Specifically, we find that K has the following form:
$K_A$
in the statement of the assumption. Specifically, we find that K has the following form:
Without additional assumptions on the max-stable copula, i.e. of the exponent measure V, it seems impossible to find the form of the location functional a to make K, in (42), independent of
![]() ${\boldsymbol{z}}_{1\,:\,k-1}$
, or to know whether such a functional even exists. Without Assumption
${\boldsymbol{z}}_{1\,:\,k-1}$
, or to know whether such a functional even exists. Without Assumption
![]() $A_2$
we cannot use Corollary 1 to find the norming functions for
$A_2$
we cannot use Corollary 1 to find the norming functions for
![]() $t\ge k$
. To get around this problem, here we can make an additional assumption about V, which ensures that K is independent of
$t\ge k$
. To get around this problem, here we can make an additional assumption about V, which ensures that K is independent of
![]() ${\boldsymbol{z}}_{1\,:\,k-1}$
and thus that Assumption
${\boldsymbol{z}}_{1\,:\,k-1}$
and thus that Assumption
![]() $A_2$
holds. The new assumption exploits the property that both
$A_2$
holds. The new assumption exploits the property that both
![]() $V_{0\,:\,k-1}(\cdot,\infty)$
and
$V_{0\,:\,k-1}(\cdot,\infty)$
and
![]() $V_{0\,:\,k-1}(\cdot)$
are
$V_{0\,:\,k-1}(\cdot)$
are
![]() $-(k+1)$
-homogeneous functions, so the map
$-(k+1)$
-homogeneous functions, so the map
is 0-homogeneous, and this latter property restricts the possible forms the function
![]() $V_{0\,:\,k-1}$
can take. One such simple form is given by Property
$V_{0\,:\,k-1}$
can take. One such simple form is given by Property
![]() $K_1$
, which holds for a wide variety of parametric models for the exponent measure, including the logistic dependence and Hüsler–Reiss dependence structures discussed below.
$K_1$
, which holds for a wide variety of parametric models for the exponent measure, including the logistic dependence and Hüsler–Reiss dependence structures discussed below.
Assumption 8. There exist a continuous function
![]() $a_P\,:\,{{{\mathbb{R}}}}_+^k\to {{{\mathbb{R}}}}_+$
which is 1-homogeneous, and a non-degenerate distribution function
$a_P\,:\,{{{\mathbb{R}}}}_+^k\to {{{\mathbb{R}}}}_+$
which is 1-homogeneous, and a non-degenerate distribution function
![]() $K_P$
on
$K_P$
on
![]() ${{{\mathbb{R}}}}_+$
, such that the following hold:
${{{\mathbb{R}}}}_+$
, such that the following hold:
-
(i)
 $K_P^\leftarrow(p^\star)=1$
for some
$K_P^\leftarrow(p^\star)=1$
for some
 $p^\star\in(0,1)$
, where
$p^\star\in(0,1)$
, where
 $K_P^\leftarrow(p)=\inf\{x\in{{{\mathbb{R}}}}_+ \,:\, K_P(x)> p\}$
;
$K_P^\leftarrow(p)=\inf\{x\in{{{\mathbb{R}}}}_+ \,:\, K_P(x)> p\}$
; -
(ii)
 $V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, y_k) = V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1} , \infty) \, K_P\{y_k/a_P({\boldsymbol{y}}_{0\,:\,k-1})\}$
, for all
$V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, y_k) = V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1} , \infty) \, K_P\{y_k/a_P({\boldsymbol{y}}_{0\,:\,k-1})\}$
, for all
 ${\boldsymbol{y}}_{0\,:\,k}\in{{{\mathbb{R}}}}_+^{k}$
.
${\boldsymbol{y}}_{0\,:\,k}\in{{{\mathbb{R}}}}_+^{k}$
.
When Assumption 8 holds, additional information about the location functional a and the limit distribution
![]() $K_A$
of Corollary 1 can be given. This is established in Proposition 3 below.
$K_A$
of Corollary 1 can be given. This is established in Proposition 3 below.
Proposition 3. Suppose that for a max-stable distribution with exponent function V, Assumption 8 holds. Let
![]() $a({\boldsymbol{x}}_{0\,:\,k-1})=\log [a_P\{\exp ({\boldsymbol{x}}_{0\,:\,k-1})\}]$
,
$a({\boldsymbol{x}}_{0\,:\,k-1})=\log [a_P\{\exp ({\boldsymbol{x}}_{0\,:\,k-1})\}]$
,
![]() ${\boldsymbol{x}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
, and assume that there exists a right-inverse
${\boldsymbol{x}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
, and assume that there exists a right-inverse
![]() ${{{\mathbb{R}}}}\times{{{\mathbb{R}}}}^k_+\ni (q,{\boldsymbol{y}}_{0\,:\,k-1})\mapsto V_{0\,:\,k-1}^\leftarrow(q;{\boldsymbol{y}}_{0\,:\,k-1})\in{{{\mathbb{R}}}}_+$
such that
${{{\mathbb{R}}}}\times{{{\mathbb{R}}}}^k_+\ni (q,{\boldsymbol{y}}_{0\,:\,k-1})\mapsto V_{0\,:\,k-1}^\leftarrow(q;{\boldsymbol{y}}_{0\,:\,k-1})\in{{{\mathbb{R}}}}_+$
such that
![]() $V_{0\,:\,k-1}\big\{{\boldsymbol{y}}_{0\,:\,k-1}, V_{0\,:\,k-1}^{\leftarrow}(q;{\boldsymbol{y}}_{0\,:\,k-1})\big\} = q$
for all q and
$V_{0\,:\,k-1}\big\{{\boldsymbol{y}}_{0\,:\,k-1}, V_{0\,:\,k-1}^{\leftarrow}(q;{\boldsymbol{y}}_{0\,:\,k-1})\big\} = q$
for all q and
![]() ${\boldsymbol{y}}_{0\,:\,k-1}$
in the domain of
${\boldsymbol{y}}_{0\,:\,k-1}$
in the domain of
![]() $V_{0\,:\,k-1}^{\leftarrow}$
. Then the following hold:
$V_{0\,:\,k-1}^{\leftarrow}$
. Then the following hold:
(i) The location functional a satisfies the property (19), and for all
![]() ${\boldsymbol{x}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
,
${\boldsymbol{x}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
,
(ii) Assumption 3 holds with normalizing functionals a as given by (44) and
![]() $b\equiv 1$
, and
$b\equiv 1$
, and
![]() ${K_A(x)} = K_P (e^x)$
,
${K_A(x)} = K_P (e^x)$
,
![]() $x\in{{{\mathbb{R}}}}$
.
$x\in{{{\mathbb{R}}}}$
.
(iii) For all
![]() $x\in{{{\mathbb{R}}}}$
,
$x\in{{{\mathbb{R}}}}$
,
where
![]() ${\boldsymbol{z}}_{0\,:\,k-1}^\star$
satisfies
${\boldsymbol{z}}_{0\,:\,k-1}^\star$
satisfies
![]() $a_P\big({\boldsymbol{z}}_{0\,:\,k-1}^\star\big)=1$
.
$a_P\big({\boldsymbol{z}}_{0\,:\,k-1}^\star\big)=1$
.
So, for a Markov chain with max-stable copula under the assumptions of Proposition 3, we now have new general results from Corollary 1 on the hidden tail chain, which here is identical to the tail chain, and a and
![]() $K_A$
have been derived. To help interpret these results, given the generality of the terms for a and
$K_A$
have been derived. To help interpret these results, given the generality of the terms for a and
![]() $K_A$
in Proposition 3, we now investigate two well-established multivariate extreme-value distribution dependence models which satisfy the assumptions of Section 2 and Proposition 3.
$K_A$
in Proposition 3, we now investigate two well-established multivariate extreme-value distribution dependence models which satisfy the assumptions of Section 2 and Proposition 3.
Logistic dependence: The exponent function of the
![]() $(k+1)$
-dimensional max-stable distribution with logistic dependence is given in (39), where
$(k+1)$
-dimensional max-stable distribution with logistic dependence is given in (39), where
![]() $\alpha\in(0,1)$
controls the strength of dependence, with stronger dependence as
$\alpha\in(0,1)$
controls the strength of dependence, with stronger dependence as
![]() $\alpha$
decreases. The case
$\alpha$
decreases. The case
![]() $\alpha=1$
is excluded as that corresponds to independence. [Reference Heffernan and Tawn9] show that the initial limiting distribution (41) is
$\alpha=1$
is excluded as that corresponds to independence. [Reference Heffernan and Tawn9] show that the initial limiting distribution (41) is
in addition to having
![]() $a_i(v)=v, b_i(v)=1$
for
$a_i(v)=v, b_i(v)=1$
for
![]() $i=1,\ldots ,k-1$
. Appendix A.8 shows that Assumption 3 holds with normalizing functionals
$i=1,\ldots ,k-1$
. Appendix A.8 shows that Assumption 3 holds with normalizing functionals
and the transition probability kernel of the renormalized Markov chain converges weakly to the distribution
Corollary 1 then asserts that the suitable normalization is
![]() $a_t(v)=v$
,
$a_t(v)=v$
,
![]() $b_t(v)=1$
for
$b_t(v)=1$
for
![]() $t\geq k$
, which leads to the hidden tail chain
$t\geq k$
, which leads to the hidden tail chain
where
![]() $\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
$\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
![]() $K_A$
. Note that the hidden tail chain can also be expressed as
$K_A$
. Note that the hidden tail chain can also be expressed as
Here the hidden tail chain is identical to the tail chain, as
![]() $a_t(x)=x$
and
$a_t(x)=x$
and
![]() $b_t(x)=1$
for all
$b_t(x)=1$
for all
![]() $t=1,2,\ldots$
. When
$t=1,2,\ldots$
. When
![]() $k=1$
, the tail chain can be seen to reduce to the random-walk results of [Reference Perfekt22, Reference Smith32], but when
$k=1$
, the tail chain can be seen to reduce to the random-walk results of [Reference Perfekt22, Reference Smith32], but when
![]() $k>1$
, the tail chain behaves like a random walk with an extra additive factor which depends in a nonlinear way on the ‘profile’
$k>1$
, the tail chain behaves like a random walk with an extra additive factor which depends in a nonlinear way on the ‘profile’
![]() $ {{Z}}_{t-k}{\textbf{1}}_{k-1}- {\boldsymbol{Z}}_{t-k+1\,:\,t-1}$
of the previous
$ {{Z}}_{t-k}{\textbf{1}}_{k-1}- {\boldsymbol{Z}}_{t-k+1\,:\,t-1}$
of the previous
![]() $k-1$
values.
$k-1$
values.
Hüsler–Reiss dependence: The exponent function of the
![]() $(k+1)$
-dimensional max-stable distribution with Hüsler–Reiss dependence is
$(k+1)$
-dimensional max-stable distribution with Hüsler–Reiss dependence is
 \begin{eqnarray*} V({\boldsymbol{y}}_{0\,:\,k})&=& \sum_{i=0}^k \frac{1}{y_i}\,\Phi_{k}\big[\big\{\log(y_j/y_i) + \sigma^2 - \sigma_{ij}\big\}_{j\neq i};\,\boldsymbol{\Sigma}^{(i)}\big], \qquad {\boldsymbol{y}}_{0\,:\,k}\in{{{\mathbb{R}}}}_+^{k+1}, \end{eqnarray*}
\begin{eqnarray*} V({\boldsymbol{y}}_{0\,:\,k})&=& \sum_{i=0}^k \frac{1}{y_i}\,\Phi_{k}\big[\big\{\log(y_j/y_i) + \sigma^2 - \sigma_{ij}\big\}_{j\neq i};\,\boldsymbol{\Sigma}^{(i)}\big], \qquad {\boldsymbol{y}}_{0\,:\,k}\in{{{\mathbb{R}}}}_+^{k+1}, \end{eqnarray*}
where
![]() $\Phi_{k}(\,\cdot\, ;\,\boldsymbol{\Sigma}^{(i)})$
denotes the multivariate normal distribution function with mean zero and covariance matrix
$\Phi_{k}(\,\cdot\, ;\,\boldsymbol{\Sigma}^{(i)})$
denotes the multivariate normal distribution function with mean zero and covariance matrix
![]() $\boldsymbol{\Sigma}^{(i)} = {\boldsymbol{T}}_i\, \boldsymbol{\Sigma} \, {\boldsymbol{T}}_i^\top$
, for
$\boldsymbol{\Sigma}^{(i)} = {\boldsymbol{T}}_i\, \boldsymbol{\Sigma} \, {\boldsymbol{T}}_i^\top$
, for
![]() $\boldsymbol{\Sigma} = (\sigma_{ij})_{i,j=0}^k$
a positive definite Toeplitz covariance matrix with common diagonal elements
$\boldsymbol{\Sigma} = (\sigma_{ij})_{i,j=0}^k$
a positive definite Toeplitz covariance matrix with common diagonal elements
![]() $\sigma_{ii}=\sigma^2$
, and
$\sigma_{ii}=\sigma^2$
, and
![]() ${\boldsymbol{T}}_i$
is a
${\boldsymbol{T}}_i$
is a
![]() $k\times (k+1)$
matrix with the
$k\times (k+1)$
matrix with the
![]() $(i+1)$
th column having
$(i+1)$
th column having
![]() $-1$
for each entry and the other columns being the k standard orthonormal basis vectors of
$-1$
for each entry and the other columns being the k standard orthonormal basis vectors of
![]() ${{{\mathbb{R}}}}^k$
, that is,
${{{\mathbb{R}}}}^k$
, that is,
 \begin{align*} {\boldsymbol{T}}_i = \left(\begin{matrix} 1& \quad 0& \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 0\\ 0& \quad 1& \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 0 \\ \vdots& \quad \vdots & & \quad \vdots & \quad \vdots & \quad \vdots & &\quad \vdots \\ 0 & \quad 0 & \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 1 \end{matrix}\right),\qquad i=0,\ldots,k. \end{align*}
\begin{align*} {\boldsymbol{T}}_i = \left(\begin{matrix} 1& \quad 0& \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 0\\ 0& \quad 1& \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 0 \\ \vdots& \quad \vdots & & \quad \vdots & \quad \vdots & \quad \vdots & &\quad \vdots \\ 0 & \quad 0 & \quad \cdots & \quad 0 & \quad -1 & \quad 0 & \quad \cdots & \quad 1 \end{matrix}\right),\qquad i=0,\ldots,k. \end{align*}
The matrix
![]() $\boldsymbol{\Sigma}$
controls the strength of dependence, with larger values for
$\boldsymbol{\Sigma}$
controls the strength of dependence, with larger values for
![]() $\sigma_{ij}$
indicating stronger dependence between the associated elements of the random vector. The initial limiting distribution (41) is
$\sigma_{ij}$
indicating stronger dependence between the associated elements of the random vector. The initial limiting distribution (41) is
![]() $G({\boldsymbol{x}})=\Phi_{k-1}[{\boldsymbol{x}}-\{-\text{diag}(\boldsymbol{\Sigma}^{(0)})/2\};\boldsymbol{\Sigma}^{(0)}]$
,
$G({\boldsymbol{x}})=\Phi_{k-1}[{\boldsymbol{x}}-\{-\text{diag}(\boldsymbol{\Sigma}^{(0)})/2\};\boldsymbol{\Sigma}^{(0)}]$
,
![]() ${\boldsymbol{x}} \in {{{\mathbb{R}}}}^{k-1}$
, in addition to having
${\boldsymbol{x}} \in {{{\mathbb{R}}}}^{k-1}$
, in addition to having
![]() $a_i(v)=v$
,
$a_i(v)=v$
,
![]() $b_i(v)=1$
for
$b_i(v)=1$
for
![]() $i=1,\ldots ,k-1$
[Reference Engelke, Malinowski, Kabluchko and Schlather7]. Appendix A.9 shows that Assumption 3 holds with normalizing functionals
$i=1,\ldots ,k-1$
[Reference Engelke, Malinowski, Kabluchko and Schlather7]. Appendix A.9 shows that Assumption 3 holds with normalizing functionals
where the quantities
![]() $\tau$
,
$\tau$
,
![]() ${\boldsymbol{q}}$
,
${\boldsymbol{q}}$
,
![]() ${\boldsymbol{C}}$
,
${\boldsymbol{C}}$
,
![]() ${\boldsymbol{K}}_{10}$
, and
${\boldsymbol{K}}_{10}$
, and
![]() ${\boldsymbol{K}}_{01}$
are constants with respect to
${\boldsymbol{K}}_{01}$
are constants with respect to
![]() ${\boldsymbol{u}}$
but depend on the parameters of
${\boldsymbol{u}}$
but depend on the parameters of
![]() $\Sigma$
; they are defined in Appendix A.9. The transition probability kernel of the renormalized Markov chain converges weakly to the distribution
$\Sigma$
; they are defined in Appendix A.9. The transition probability kernel of the renormalized Markov chain converges weakly to the distribution
Corollary 1 asserts that a suitable normalization is
![]() $a_t(v)=v$
,
$a_t(v)=v$
,
![]() $b_t(v)=1$
for
$b_t(v)=1$
for
![]() $t\geq k$
, which leads to the hidden tail chain (identical to the tail chain)
$t\geq k$
, which leads to the hidden tail chain (identical to the tail chain)
where
![]() $\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
$\{\varepsilon_t\}_{t=k}^\infty$
is a sequence of i.i.d. random variables with distribution
![]() $K_A$
. Note that the tail chain can also be expressed as
$K_A$
. Note that the tail chain can also be expressed as
which shows, similarly to the case of the logistic copula, that the tail chain behaves like a random walk with an extra factor which depends linearly on the ‘profile’
![]() ${{Z}}_{t-k} {\textbf{1}}_{k-1}-{\boldsymbol{Z}}_{t-k+1\,:\,t-1}$
of the previous
${{Z}}_{t-k} {\textbf{1}}_{k-1}-{\boldsymbol{Z}}_{t-k+1\,:\,t-1}$
of the previous
![]() $k-1$
values; in this respect it differs from the previous example.
$k-1$
values; in this respect it differs from the previous example.
Panels (c) and (d) in Figure 1 show almost linear behaviour for two special cases of the tail chains presented. Although the copulas used to derive both (hidden) tail chains have the same extremal coefficient see [Reference Schlather and Tawn28], ensuring that the core level of extremal dependence is common to both, the decay rates of the two processes are markedly different. This shows that the type of drift function and distribution for the innovation term
![]() $\varepsilon_t$
affect the characteristics of the transition from an extreme state to the main body of the process.
$\varepsilon_t$
affect the characteristics of the transition from an extreme state to the main body of the process.
Example 4. (Multivariate extreme value copula with asymmetric logistic structure [Reference Tawn33].) This is a second-order Markov process for which Assumptions 2 and 3 fail to hold, and it has a more complicated structure than we have covered so far in studying weak convergence on
![]() ${{{\mathbb{R}}}}^k$
. In this example, the weak convergences in Assumptions 2 and 3 no longer hold on
${{{\mathbb{R}}}}^k$
. In this example, the weak convergences in Assumptions 2 and 3 no longer hold on
![]() ${{{\mathbb{R}}}}^{k-1}$
and
${{{\mathbb{R}}}}^{k-1}$
and
![]() ${{{\mathbb{R}}}}$
(cf. Remark 1), but on
${{{\mathbb{R}}}}$
(cf. Remark 1), but on
![]() $\overline{{{{\mathbb{R}}}}}^{k-1}$
and
$\overline{{{{\mathbb{R}}}}}^{k-1}$
and
![]() $\overline{{{{\mathbb{R}}}}}$
, respectively. The example is a special case of a stationary Markov chain with transition probability kernel (33) and exponent function given by
$\overline{{{{\mathbb{R}}}}}$
, respectively. The example is a special case of a stationary Markov chain with transition probability kernel (33) and exponent function given by
 \begin{align} V(x_0,x_1,x_2) & = \theta_0\, x_0^{-1} + \theta_1\, x_1^{-1}+ \theta_{2}\, x_2^{-1} \nonumber\\ & \quad + \theta_{01}\Big\{ \Big(x_0^{-1/\nu_{01}}+ x_1^{-1/\nu_{01}}\Big)^{\nu_{01}} + \Big(x_1^{-1/\nu_{01}}+ x_2^{-1/\nu_{01}}\Big)^{\nu_{01}}\Big\} \nonumber\\ &\quad + \theta_{01} \Big(x_0^{-1/\nu_{02}}+x_2^{-1/\nu_{02}} \Big)^{\nu_{02}} \nonumber\\ &\quad +\theta_{012} \Big(x_0^{-1/\nu_{012}}+ + x_1^{-1/\nu_{012}}+x_2^{-1/\nu_{012}}\Big)^{1/\nu_{012} }, \end{align}
\begin{align} V(x_0,x_1,x_2) & = \theta_0\, x_0^{-1} + \theta_1\, x_1^{-1}+ \theta_{2}\, x_2^{-1} \nonumber\\ & \quad + \theta_{01}\Big\{ \Big(x_0^{-1/\nu_{01}}+ x_1^{-1/\nu_{01}}\Big)^{\nu_{01}} + \Big(x_1^{-1/\nu_{01}}+ x_2^{-1/\nu_{01}}\Big)^{\nu_{01}}\Big\} \nonumber\\ &\quad + \theta_{01} \Big(x_0^{-1/\nu_{02}}+x_2^{-1/\nu_{02}} \Big)^{\nu_{02}} \nonumber\\ &\quad +\theta_{012} \Big(x_0^{-1/\nu_{012}}+ + x_1^{-1/\nu_{012}}+x_2^{-1/\nu_{012}}\Big)^{1/\nu_{012} }, \end{align}
where
![]() $\nu_A \in (0,1)$
for any
$\nu_A \in (0,1)$
for any
![]() $A\in 2^{\{0,1,2\}}{{\setminus}} \emptyset$
, and
$A\in 2^{\{0,1,2\}}{{\setminus}} \emptyset$
, and
with
![]() $\theta_0, \theta_1, \theta_2, \theta_{01}, \theta_{02}, \theta_{012} >0.$
$\theta_0, \theta_1, \theta_2, \theta_{01}, \theta_{02}, \theta_{012} >0.$
Although this distribution does not satisfy the assumptions of Section 2, the strategy that is implemented to find the normalizing functions and hidden tail chain is similar to the strategy presented in Section 5.1. In particular, the initial distribution of the Markov process is
![]() $F_{01}(x_0, x_1)=F_{012}(x_0,x_1,\infty)=\exp\{-V(y_0,y_1,\infty)\}$
, with
$F_{01}(x_0, x_1)=F_{012}(x_0,x_1,\infty)=\exp\{-V(y_0,y_1,\infty)\}$
, with
![]() $(y_0, y_1)$
defined in (30). It can be seen that the transition probability kernel
$(y_0, y_1)$
defined in (30). It can be seen that the transition probability kernel
![]() $\pi(x_0, x_1)= -y_0^2 \,V_0(y_0,y_1,\infty) \exp(y_0^{-1}-V(y_0,y_1,\infty))$
associated with the conditional distribution of
$\pi(x_0, x_1)= -y_0^2 \,V_0(y_0,y_1,\infty) \exp(y_0^{-1}-V(y_0,y_1,\infty))$
associated with the conditional distribution of
![]() $X_1 \mid X_0$
converges with two distinct normalizations, that is,
$X_1 \mid X_0$
converges with two distinct normalizations, that is,
![]() $\pi(v, dx){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_0(dx)$
and
$\pi(v, dx){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_0(dx)$
and
![]() $\pi(v, v+dx){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_1(dx)$
as
$\pi(v, v+dx){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_1(dx)$
as
![]() $v\to\infty$
, to the distributions
$v\to\infty$
, to the distributions
![]() $K_0=(\theta_0+\theta_{02}) \, F_E + (\theta_{01}+\theta_{012})\,\delta_{+\infty}$
and
$K_0=(\theta_0+\theta_{02}) \, F_E + (\theta_{01}+\theta_{012})\,\delta_{+\infty}$
and
![]() $K_1 = (\theta_0+\theta_{02})\, \delta_{-\infty} + \theta_{01} \,G_{01} + \theta_{012} \, G_{012}$
, respectively, where
$K_1 = (\theta_0+\theta_{02})\, \delta_{-\infty} + \theta_{01} \,G_{01} + \theta_{012} \, G_{012}$
, respectively, where
![]() $F_E(x)=(1-\exp({-}x))_+$
,
$F_E(x)=(1-\exp({-}x))_+$
,
![]() $G_{A}(x)=(1+\exp({-}x/\nu_A))^{\nu_A-1}$
, and
$G_{A}(x)=(1+\exp({-}x/\nu_A))^{\nu_A-1}$
, and
![]() $\delta_x$
is a point mass at
$\delta_x$
is a point mass at
![]() $x \in [{-}\infty, \infty]$
[cf. Example 5 in Reference Papastathopoulos, Strokorb, Tawn and Butler20]. The distributions
$x \in [{-}\infty, \infty]$
[cf. Example 5 in Reference Papastathopoulos, Strokorb, Tawn and Butler20]. The distributions
![]() $K_0$
and
$K_0$
and
![]() $K_1$
have their entire mass on
$K_1$
have their entire mass on
![]() $(0,\infty]$
and
$(0,\infty]$
and
![]() $[{-}\infty,\infty)$
, respectively. In the first and second normalizations, a mass of size
$[{-}\infty,\infty)$
, respectively. In the first and second normalizations, a mass of size
![]() $(1-\theta_{01}-\theta_{012})$
escapes to
$(1-\theta_{01}-\theta_{012})$
escapes to
![]() $+\infty$
and a mass of size
$+\infty$
and a mass of size
![]() $(\theta_0+\theta_{02})$
escapes to
$(\theta_0+\theta_{02})$
escapes to
![]() $-\infty$
, respectively. As explained by [Reference Papastathopoulos, Strokorb, Tawn and Butler20], the reason for this behaviour is that the separate normalizations are related to two different modes of the conditional distribution of
$-\infty$
, respectively. As explained by [Reference Papastathopoulos, Strokorb, Tawn and Butler20], the reason for this behaviour is that the separate normalizations are related to two different modes of the conditional distribution of
![]() $X_{1}\mid X_0$
. This phenomenon also manifests in the conditional distribution of
$X_{1}\mid X_0$
. This phenomenon also manifests in the conditional distribution of
![]() $X_2\mid \{X_0, X_1\}$
, which is given by
$X_2\mid \{X_0, X_1\}$
, which is given by
where
![]() $g(f_1,f_2,f_3)(x) \,:\!=\, g(f_1(x),f_2(x), f_3(x))$
for maps g and
$g(f_1,f_2,f_3)(x) \,:\!=\, g(f_1(x),f_2(x), f_3(x))$
for maps g and
![]() $f_i$
,
$f_i$
,
![]() $i=1,2,3$
. Here the problem is more complex, with this transition probability kernel converging with
$i=1,2,3$
. Here the problem is more complex, with this transition probability kernel converging with
![]() $2\,(2^k-1)=6$
distinct normalizations. Letting
$2\,(2^k-1)=6$
distinct normalizations. Letting
 \begin{align} a_{11,1}(v_1,v_2) &= -\nu_{012}\log\{\exp({-}v_1/\nu_{012})+\exp({-}v_2/\nu_{012})\},\nonumber\\ a_{10,1}(v_1,v_2) &= v_1, a_{01,1}(v_1,v_2) =v_2, \\ a_{11,0}(v_1,v_2) &= a_{01,0}(v_1,v_2) = a_{10,0}(v_1,v_2) = 0\nonumber, \end{align}
\begin{align} a_{11,1}(v_1,v_2) &= -\nu_{012}\log\{\exp({-}v_1/\nu_{012})+\exp({-}v_2/\nu_{012})\},\nonumber\\ a_{10,1}(v_1,v_2) &= v_1, a_{01,1}(v_1,v_2) =v_2, \\ a_{11,0}(v_1,v_2) &= a_{01,0}(v_1,v_2) = a_{10,0}(v_1,v_2) = 0\nonumber, \end{align}
one can show that for
![]() $(x_0,x_1)\in {{{\mathbb{R}}}}^2$
and as
$(x_0,x_1)\in {{{\mathbb{R}}}}^2$
and as
![]() $v\to \infty$
,
$v\to \infty$
,
 \begin{eqnarray*} \pi((v+x_0, v+x_1), a_{11,1}(v+x_0, v+x_1) + dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,1\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((v+x_0, v+x_1), a_{11,0}(v+x_0, v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,1\},\{0\}}(dy;x_0,x_1)& \quad \text{on $(0,\infty]$},\\ \pi((v+x_0, x_1), a_{10,1}(v+x_0, x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,0\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((v+x_0, x_1), a_{10,0}(v+x_0, x_1) + dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,0\},\{0\}}(dy;x_0,x_1)& \quad \text{on $(0,\infty]$},\\ \pi((x_0, v+x_1), a_{01,1}(x_0,v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{0,0\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((x_0, v+x_1), a_{01,0}(x_0,v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{0,1\},\{0\}}(dy;x_0,x_1) & \quad \text{on $(0,\infty]$}, \end{eqnarray*}
\begin{eqnarray*} \pi((v+x_0, v+x_1), a_{11,1}(v+x_0, v+x_1) + dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,1\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((v+x_0, v+x_1), a_{11,0}(v+x_0, v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,1\},\{0\}}(dy;x_0,x_1)& \quad \text{on $(0,\infty]$},\\ \pi((v+x_0, x_1), a_{10,1}(v+x_0, x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,0\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((v+x_0, x_1), a_{10,0}(v+x_0, x_1) + dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{1,0\},\{0\}}(dy;x_0,x_1)& \quad \text{on $(0,\infty]$},\\ \pi((x_0, v+x_1), a_{01,1}(x_0,v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{0,0\},\{1\}}(dy;x_0,x_1)& \quad \text{on $[{-}\infty,\infty)$},\\ \pi((x_0, v+x_1), a_{01,0}(x_0,v+x_1)+dy){{\,\overset {\mathrm {w} }{\longrightarrow }\,}} K_{\{0,1\},\{0\}}(dy;x_0,x_1) & \quad \text{on $(0,\infty]$}, \end{eqnarray*}
where the limiting measures are given by
for
![]() $A\in \{0,1\}^2{{\setminus}} \{0,0\}$
, with
$A\in \{0,1\}^2{{\setminus}} \{0,0\}$
, with
 \begin{equation*} m_{A}(x_0,x_1) = \begin{cases}\Big\{1 + \big(\frac{\kappa_{012}}{\kappa_{01}}\big) e^{\lambda(x_0+x_1)}\,{\displaystyle W_{\nu_{01}-1}(e^{x_0},e^{x_1}\,;\,\nu_{01}) / W_{\nu_{012}-1}(e^{x_0},e^{x_1}\,;\,\nu_{012})}\Big\}^{-1},& \\ \theta_{0}/(\theta_0+\theta_{02}), & \\ \theta_{1}/(\theta_1+\theta_{01}), & \end{cases}\end{equation*}
\begin{equation*} m_{A}(x_0,x_1) = \begin{cases}\Big\{1 + \big(\frac{\kappa_{012}}{\kappa_{01}}\big) e^{\lambda(x_0+x_1)}\,{\displaystyle W_{\nu_{01}-1}(e^{x_0},e^{x_1}\,;\,\nu_{01}) / W_{\nu_{012}-1}(e^{x_0},e^{x_1}\,;\,\nu_{012})}\Big\}^{-1},& \\ \theta_{0}/(\theta_0+\theta_{02}), & \\ \theta_{1}/(\theta_1+\theta_{01}), & \end{cases}\end{equation*}
for
![]() $A=\{1,1\}$
,
$A=\{1,1\}$
,
![]() $A=\{1,0\}$
, and
$A=\{1,0\}$
, and
![]() $A=\{0,1\}$
, respectively, and
$A=\{0,1\}$
, respectively, and
 \begin{align*} G_{\{1,1\},\{1\}}(y\,;\,x_0,x_1) &= W_2\{1, \exp(y)\,;\,\nu_{012}\},\\ G_{\{1,1\},\{0\}}(y\,;\,x_0,x_1) &= F_E(y),\\ G_{\{1,0\},\{1\}}(y\,;\,x_0,x_1) &= W_1\{1,\exp(y)\,;\,\nu_{02}\},\\ G_{\{1,0\},\{0\}}(y\,;\,x_0,x_1) &= [\theta_1 + \theta_{01} \{1 + W_1(1, T(y)/T(x_1);\nu_{01})\} \\&\qquad\qquad\qquad +\theta_{012} W_1(1, T(y)/T(x_1)\,;\,\nu_{012})] g_{10}(x, y),\\ G_{\{0,1\},\{1\}}(y\,;\,x_0,x_1) &= W_1\{1, \exp(y)\,;\,\nu_{01}\},\\ G_{\{0,1\},\{0\}}(y\,;\,x_0,x_1) &= [\theta_0 + \theta_{01} +\theta_{02} W_1(1, T(y)/T(x_0)\,;\,\nu_{02}) \\&\qquad \qquad \qquad +\theta_{012} W_1(1, T(y)/T(x_0)\,;\,\nu_{012})] g_{01}(x, y).\end{align*}
\begin{align*} G_{\{1,1\},\{1\}}(y\,;\,x_0,x_1) &= W_2\{1, \exp(y)\,;\,\nu_{012}\},\\ G_{\{1,1\},\{0\}}(y\,;\,x_0,x_1) &= F_E(y),\\ G_{\{1,0\},\{1\}}(y\,;\,x_0,x_1) &= W_1\{1,\exp(y)\,;\,\nu_{02}\},\\ G_{\{1,0\},\{0\}}(y\,;\,x_0,x_1) &= [\theta_1 + \theta_{01} \{1 + W_1(1, T(y)/T(x_1);\nu_{01})\} \\&\qquad\qquad\qquad +\theta_{012} W_1(1, T(y)/T(x_1)\,;\,\nu_{012})] g_{10}(x, y),\\ G_{\{0,1\},\{1\}}(y\,;\,x_0,x_1) &= W_1\{1, \exp(y)\,;\,\nu_{01}\},\\ G_{\{0,1\},\{0\}}(y\,;\,x_0,x_1) &= [\theta_0 + \theta_{01} +\theta_{02} W_1(1, T(y)/T(x_0)\,;\,\nu_{02}) \\&\qquad \qquad \qquad +\theta_{012} W_1(1, T(y)/T(x_0)\,;\,\nu_{012})] g_{01}(x, y).\end{align*}
Here, the function T is defined in (30),
![]() $\kappa_A = \theta_{A}\,(\nu_{A}-1)/\nu_{A}$
,
$\kappa_A = \theta_{A}\,(\nu_{A}-1)/\nu_{A}$
,
![]() $W_p(x, y\,;\,\nu)=(x^{-1/\nu} + y^{-1/\nu})^{\nu-p}$
, with
$W_p(x, y\,;\,\nu)=(x^{-1/\nu} + y^{-1/\nu})^{\nu-p}$
, with
![]() $x,y>0$
,
$x,y>0$
,
![]() $p \in {{{\mathbb{R}}}}$
,
$p \in {{{\mathbb{R}}}}$
,
![]() $\nu \in(0,1)$
,
$\nu \in(0,1)$
,
To help explain the necessity for requiring the normalizing functionals (47) to describe the evolution of an extreme episode after witnessing an extreme event in this second-order Markov process, it is useful to consider the behaviour of the spectral measure H, defined in Equation (31), for the initial distribution
![]() $F_{012}$
of this process. Here, the spectral measure H places a mass of size
$F_{012}$
of this process. Here, the spectral measure H places a mass of size
![]() $\lvert A\lvert\,\theta_A$
on each subface
$\lvert A\lvert\,\theta_A$
on each subface
![]() $A\in\mathscr{P}([2])$
of
$A\in\mathscr{P}([2])$
of
![]() ${{\Delta}}^2$
[Reference Coles and Tawn4], which implies that different subsets of the variables
${{\Delta}}^2$
[Reference Coles and Tawn4], which implies that different subsets of the variables
![]() $(X_{t-2},X_{t-1},X_t)$
can take their largest values simultaneously; see for example [Reference Simpson, Wadsworth and Tawn30]. Hence, if the Markov process is in an extreme episode at time
$(X_{t-2},X_{t-1},X_t)$
can take their largest values simultaneously; see for example [Reference Simpson, Wadsworth and Tawn30]. Hence, if the Markov process is in an extreme episode at time
![]() $t-1$
,
$t-1$
,
![]() $t\geq 3$
, then it follows that there are four possibilities for the states
$t\geq 3$
, then it follows that there are four possibilities for the states
![]() $(X_{t-2}, X_{t-1})$
; that is, either the variables
$(X_{t-2}, X_{t-1})$
; that is, either the variables
![]() $X_{t-2}$
and
$X_{t-2}$
and
![]() $ X_{t-1}$
are simultaneously extreme or just one of them is. Consequently, there are two possibilities for the state of the process at time t; that is, the variable
$ X_{t-1}$
are simultaneously extreme or just one of them is. Consequently, there are two possibilities for the state of the process at time t; that is, the variable
![]() $X_t$
can be either extreme or not, and this is demonstrated by bimodality in the transition probability kernel under all four distinct possibilities for the states
$X_t$
can be either extreme or not, and this is demonstrated by bimodality in the transition probability kernel under all four distinct possibilities for the states
![]() $X_{t-2}$
and
$X_{t-2}$
and
![]() $X_{t-1}$
. In total, this gives rise to six distinct possibilities which necessitate an ‘event-specific’ normalizing functional to guarantee the weak convergence of the transition probability kernel. This justifies the labelling of the functionals in (47), where the label (A,b) appearing in the subscript, with
$X_{t-1}$
. In total, this gives rise to six distinct possibilities which necessitate an ‘event-specific’ normalizing functional to guarantee the weak convergence of the transition probability kernel. This justifies the labelling of the functionals in (47), where the label (A,b) appearing in the subscript, with
![]() $A\in \{0,1\}^2$
and
$A\in \{0,1\}^2$
and
![]() $b\in \{0,1\}$
, indicates transitioning from one of four possible configurations (A) at times
$b\in \{0,1\}$
, indicates transitioning from one of four possible configurations (A) at times
![]() $t-2$
and
$t-2$
and
![]() $t-1$
into two possible configurations (b) at time t—with 1 indicating that the state is extreme and 0 otherwise. The case where the Markov process is in an extreme episode at time
$t-1$
into two possible configurations (b) at time t—with 1 indicating that the state is extreme and 0 otherwise. The case where the Markov process is in an extreme episode at time
![]() $t-1$
, for
$t-1$
, for
![]() $t=2$
, is handled similarly. There we note that
$t=2$
, is handled similarly. There we note that
![]() $X_0$
is already extreme, by virtue of the conditioning, and hence there are two possibilities for
$X_0$
is already extreme, by virtue of the conditioning, and hence there are two possibilities for
![]() $X_0$
and
$X_0$
and
![]() $X_1$
; that is, either
$X_1$
; that is, either
![]() $X_1$
is extreme or it is not.
$X_1$
is extreme or it is not.
Although complex, these modes can be identified by any line determined by the loci of points
![]() $(\max(x_{t-2},x_{t-1}), \zeta \, \max(x_{t-2}, x_{t-1}))$
, where
$(\max(x_{t-2},x_{t-1}), \zeta \, \max(x_{t-2}, x_{t-1}))$
, where
![]() $x_{t-2},x_{t-1} \in {{{\mathbb{R}}}}$
, for some
$x_{t-2},x_{t-1} \in {{{\mathbb{R}}}}$
, for some
![]() $\zeta\in(0,1)$
, in the distribution of
$\zeta\in(0,1)$
, in the distribution of
![]() $X_{t}\mid \max\{X_{t-2},X_{t-1}\}>v$
; see panels (b), (c), and (d) of Figure 2, where v is taken equal to 9. This facilitates accounting for the identification of the normalizing functionals by introducing the stopping times,
$X_{t}\mid \max\{X_{t-2},X_{t-1}\}>v$
; see panels (b), (c), and (d) of Figure 2, where v is taken equal to 9. This facilitates accounting for the identification of the normalizing functionals by introducing the stopping times,
![]() $T_0^X = 0$
a.s., and
$T_0^X = 0$
a.s., and
where
subject to the convention
![]() $X_{-s}=0$
for
$X_{-s}=0$
for
![]() $s\in {{\mathbb{N}}}{{\setminus}}\{0\}$
; that is,
$s\in {{\mathbb{N}}}{{\setminus}}\{0\}$
; that is,
![]() $T_j^X$
, with
$T_j^X$
, with
![]() $j\geq 1$
, is the jth time that
$j\geq 1$
, is the jth time that
![]() $\zeta$
multiplied by the maximum of the previous two states is not exceeded after time 0, and the termination time
$\zeta$
multiplied by the maximum of the previous two states is not exceeded after time 0, and the termination time
![]() $T^X$
is the first time after time 0 where two consecutive states did not exceed
$T^X$
is the first time after time 0 where two consecutive states did not exceed
![]() $\zeta$
times the maximum of their respective two previous states. Define
$\zeta$
times the maximum of their respective two previous states. Define
 \begin{align*} a_1(v) = \begin{cases} v, & T^X_1 > 1, \\ 0, & T^X_1 =1, \end{cases} \quad \text{and} \quad b_t(v) = 1 \quad \text{for all $t\geq 1$}.\end{align*}
\begin{align*} a_1(v) = \begin{cases} v, & T^X_1 > 1, \\ 0, & T^X_1 =1, \end{cases} \quad \text{and} \quad b_t(v) = 1 \quad \text{for all $t\geq 1$}.\end{align*}
Then, for
![]() $t \in \big(T_{j-1}^X , T_j^X \big]$
, letting
$t \in \big(T_{j-1}^X , T_j^X \big]$
, letting
 \begin{align*} a_t(v_1,v_2) = \begin{cases} a_{11,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1\neq T_{j-1}^X$, $t-2\neq T_{j-1}^X$}, \\ a_{11,0}(v_1,v_2) & \text{if $t=T_j^X$, $t-1\neq T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{10,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1= T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{10,0}(v_1,v_2)& \text{if $t= T_j^X$, $t-1= T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{01,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1\neq T_{j-1}^X$, $t-2= T_{j-1}^X$},\\ a_{01,0}(v_1,v_2)& \text{if $t= T_j^X$, $t-1\neq T_{j-1}^X$, $t-2= T_{j-1}^X$} \end{cases}\end{align*}
\begin{align*} a_t(v_1,v_2) = \begin{cases} a_{11,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1\neq T_{j-1}^X$, $t-2\neq T_{j-1}^X$}, \\ a_{11,0}(v_1,v_2) & \text{if $t=T_j^X$, $t-1\neq T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{10,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1= T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{10,0}(v_1,v_2)& \text{if $t= T_j^X$, $t-1= T_{j-1}^X$, $t-2\neq T_{j-1}^X$},\\ a_{01,1}(v_1,v_2)& \text{if $t\neq T_j^X$, $t-1\neq T_{j-1}^X$, $t-2= T_{j-1}^X$},\\ a_{01,0}(v_1,v_2)& \text{if $t= T_j^X$, $t-1\neq T_{j-1}^X$, $t-2= T_{j-1}^X$} \end{cases}\end{align*}
yields the hidden tail chain of this process. Specifically, let
![]() $\{B_t\,:\,t=0,1,\ldots\}$
be a sequence of latent Bernoulli random variables. Define the hitting times
$\{B_t\,:\,t=0,1,\ldots\}$
be a sequence of latent Bernoulli random variables. Define the hitting times
![]() $T_j^B=\inf\{T_{j-1}^B < t \leq T^B\,:\,B_t=0\}$
with
$T_j^B=\inf\{T_{j-1}^B < t \leq T^B\,:\,B_t=0\}$
with
![]() $T_0^B=0$
a.s. and
$T_0^B=0$
a.s. and
![]() $T^B=\inf\{t \geq 2 \,:\,B_{t-1}=0,B_t=0\}$
. Then the hidden tail chain process
$T^B=\inf\{t \geq 2 \,:\,B_{t-1}=0,B_t=0\}$
. Then the hidden tail chain process
![]() $\{{{Z}}_t\}$
together with the latent Bernoulli process
$\{{{Z}}_t\}$
together with the latent Bernoulli process
![]() $\{B_t\}$
forms a second-order Markov process with initial distribution
$\{B_t\}$
forms a second-order Markov process with initial distribution
![]() $(B_0, {{Z}}_0)=(1,0)$
a.s.,
$(B_0, {{Z}}_0)=(1,0)$
a.s.,
![]() $B_1 \sim \text{Bern}(\theta_{01}+\theta_{02})$
, and
$B_1 \sim \text{Bern}(\theta_{01}+\theta_{02})$
, and
 \begin{align*} {{\mathbb{P}}}({{Z}}_1 \leq y\mid {{Z}}_0, {\boldsymbol{B}}_{0:1}) = \begin{cases} \theta_{01} \,G_{01}(y) + \theta_{012} \,G_{012}(y),& B_1 = 1,\\ F_E(y), & B_1=0. \end{cases}\end{align*}
\begin{align*} {{\mathbb{P}}}({{Z}}_1 \leq y\mid {{Z}}_0, {\boldsymbol{B}}_{0:1}) = \begin{cases} \theta_{01} \,G_{01}(y) + \theta_{012} \,G_{012}(y),& B_1 = 1,\\ F_E(y), & B_1=0. \end{cases}\end{align*}
The transition mechanism is given by
and
Panel (a) in Figure 2 illustrates a realization from a special case of this second-order Markov process. This realized path shows that after witnessing an extreme event at time
![]() $t=0$
the process transitions to the body of the process at time
$t=0$
the process transitions to the body of the process at time
![]() $t=1$
and then has two extreme states at
$t=1$
and then has two extreme states at
![]() $t=2$
and
$t=2$
and
![]() $t=3$
and two non-extreme states at
$t=3$
and two non-extreme states at
![]() $t=4$
and
$t=4$
and
![]() $t=5$
. After two non-extreme values the process has permanently transitioned to its equilibrium, that is, for
$t=5$
. After two non-extreme values the process has permanently transitioned to its equilibrium, that is, for
![]() $t=6,\ldots$
in this realization. The sampling distribution of the average termination time
$t=6,\ldots$
in this realization. The sampling distribution of the average termination time
![]() $T_B$
of the hidden tail chain is presented in panel (e), whereas the behaviour of the hidden tail chain conditioned on its terminating after eight steps, that is,
$T_B$
of the hidden tail chain is presented in panel (e), whereas the behaviour of the hidden tail chain conditioned on its terminating after eight steps, that is,
![]() $T_B=8$
, is shown in panel (f). This shows that whilst at an extreme state, the average value of
$T_B=8$
, is shown in panel (f). This shows that whilst at an extreme state, the average value of
![]() ${{Z}}_t$
is stable through time.
${{Z}}_t$
is stable through time.
Appendix A. Proofs
A.1. Preparatory results for Theorems 1 and 2
The proofs of Theorems 1 and 2 are based on Lemmas 1 and 2 below, whose proofs are similar to those of Lemmas 1 and 2 in [Reference Papastathopoulos, Strokorb, Tawn and Butler20] and are therefore omitted for brevity.
Lemma 1. Let
![]() $\{X_t\,:\,t=0,1,\ldots\}$
be a homogeneous k th-order Markov chain satisfying Assumption 3. Then, for any
$\{X_t\,:\,t=0,1,\ldots\}$
be a homogeneous k th-order Markov chain satisfying Assumption 3. Then, for any
![]() $g \in C_b({{{\mathbb{R}}}})$
and for each time step
$g \in C_b({{{\mathbb{R}}}})$
and for each time step
![]() $t=k,k+1,\ldots,$
as
$t=k,k+1,\ldots,$
as
![]() $v\to \infty$
$v\to \infty$
and the convergence holds uniformly on compact sets in the variable
![]() ${\boldsymbol{z}} \in {{{\mathbb{R}}}}^k$
.
${\boldsymbol{z}} \in {{{\mathbb{R}}}}^k$
.
Lemma 2. Let
![]() $\{X_t\,:\,t=0,1,\ldots\}$
be a homogeneous k th-order Markov chain satisfying Assumption 5. Then, for any
$\{X_t\,:\,t=0,1,\ldots\}$
be a homogeneous k th-order Markov chain satisfying Assumption 5. Then, for any
![]() $g \in C_b([0,\infty))$
and for each time step
$g \in C_b([0,\infty))$
and for each time step
![]() $t=k,k+1,\ldots$
, as
$t=k,k+1,\ldots$
, as
![]() $v\to \infty$
$v\to \infty$
and the convergence holds uniformly on compact sets in the variable
![]() ${\boldsymbol{x}} \in [\delta_1,\infty) \times \cdots \times [\delta_k, \infty)$
for any
${\boldsymbol{x}} \in [\delta_1,\infty) \times \cdots \times [\delta_k, \infty)$
for any
![]() $(\delta_1,\ldots, \delta_{k}) \in (0,\infty)^k$
.
$(\delta_1,\ldots, \delta_{k}) \in (0,\infty)^k$
.
Lemma 3. (Slight variant of [Reference Kulik and Soulier14].) Let (E,d) be a complete locally compact separable metric space and
![]() $\mu_n$
a sequence of probability measures which converges weakly to a probability measure
$\mu_n$
a sequence of probability measures which converges weakly to a probability measure
![]() $\mu$
on E as
$\mu$
on E as
![]() $n\to \infty$
.
$n\to \infty$
.
-
(i) Let
 $\varphi_n$
be a uniformly bounded sequence of measurable functions which converges uniformly on compact sets of E to a continuous function
$\varphi_n$
be a uniformly bounded sequence of measurable functions which converges uniformly on compact sets of E to a continuous function
 $\varphi$
. Then
$\varphi$
. Then
 $\varphi$
is bounded on E and
$\varphi$
is bounded on E and
 $\lim_{n\to \infty} \mu_n(\varphi_n)\to \mu(\varphi)$
.
$\lim_{n\to \infty} \mu_n(\varphi_n)\to \mu(\varphi)$
. -
(ii) Let F be a topological space. If
 $\varphi\in C_b(F\times E)$
, then the sequence of functions
$\varphi\in C_b(F\times E)$
, then the sequence of functions
 $F\ni x \mapsto \int_E \varphi(x,y)\mu_n(dy)\in{{{\mathbb{R}}}}$
converges uniformly on compact sets of F to the (necessarily continuous) function
$F\ni x \mapsto \int_E \varphi(x,y)\mu_n(dy)\in{{{\mathbb{R}}}}$
converges uniformly on compact sets of F to the (necessarily continuous) function
 $F\ni x\mapsto\int_E \varphi(x,y)\mu(dy)\in {{{\mathbb{R}}}}$
.
$F\ni x\mapsto\int_E \varphi(x,y)\mu(dy)\in {{{\mathbb{R}}}}$
.
A.2. Proofs of Theorems 1 and 2
Preliminaries. Let
![]() $a_0(v)\equiv v$
and
$a_0(v)\equiv v$
and
![]() $b_0(v)\equiv 1$
, and define
$b_0(v)\equiv 1$
, and define
We note that in our notation, when
![]() $k=1$
, the initial conditional distribution of the rescaled Markov chain is
$k=1$
, the initial conditional distribution of the rescaled Markov chain is
whereas when
![]() $k>1$
it equals the product of the right-hand side of Equation (49) with
$k>1$
it equals the product of the right-hand side of Equation (49) with
 \begin{align*} \pi_0( v_u({{z}}_0),{\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1})) \,:\!=\,{{\mathbb{P}}}\,\Bigg(\bigcap_{j=1}^{k-1}\bigg\{\frac{X_j-a_j(X_0)}{b_j(X_0)} \in d{{z}}_j\bigg\}\,\bigg | \,\frac{X_0 - u}{\sigma(u)} = {{z}}_0\Bigg).\end{align*}
\begin{align*} \pi_0( v_u({{z}}_0),{\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1})) \,:\!=\,{{\mathbb{P}}}\,\Bigg(\bigcap_{j=1}^{k-1}\bigg\{\frac{X_j-a_j(X_0)}{b_j(X_0)} \in d{{z}}_j\bigg\}\,\bigg | \,\frac{X_0 - u}{\sigma(u)} = {{z}}_0\Bigg).\end{align*}
For
![]() $j \in \{k,\ldots,t\}$
with
$j \in \{k,\ldots,t\}$
with
![]() $t\geq k \geq 1$
the transition kernels of the rescaled Markov chain can be written as
$t\geq k \geq 1$
the transition kernels of the rescaled Markov chain can be written as
 \begin{align*} & \pi({\boldsymbol{A}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-1,k}),A_j(v_u({{z}}_0),d{{z}}_j))\\& \qquad \qquad ={{\mathbb{P}}}\,\Bigg(\frac{X_j - a_j(X_0)}{b_j(X_0)} \in d {{z}}_j\,\bigg | \, \bigg\{\frac{X_{j-i}-a_{j-i}(X_0)}{b_{j-i}(X_0)} ={{z}}_{j-i}\bigg\}_{i=1,\ldots, k}\Bigg).\end{align*}
\begin{align*} & \pi({\boldsymbol{A}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-1,k}),A_j(v_u({{z}}_0),d{{z}}_j))\\& \qquad \qquad ={{\mathbb{P}}}\,\Bigg(\frac{X_j - a_j(X_0)}{b_j(X_0)} \in d {{z}}_j\,\bigg | \, \bigg\{\frac{X_{j-i}-a_{j-i}(X_0)}{b_{j-i}(X_0)} ={{z}}_{j-i}\bigg\}_{i=1,\ldots, k}\Bigg).\end{align*}
Proof of Theorem 1. Consider, for
![]() $t\geq k\geq 1$
, the measures
$t\geq k\geq 1$
, the measures
 \begin{eqnarray*} \mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t) &=& \prod_{j=k}^t \pi({\boldsymbol{A}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-k\,:\,j-1}),A_j(v_u({{z}}_0),d{{z}}_j))\\ &&\times [\pi_0( v_u({{z}}_0), {\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))]^{1(k>1)} \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{eqnarray*}
\begin{eqnarray*} \mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t) &=& \prod_{j=k}^t \pi({\boldsymbol{A}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-k\,:\,j-1}),A_j(v_u({{z}}_0),d{{z}}_j))\\ &&\times [\pi_0( v_u({{z}}_0), {\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))]^{1(k>1)} \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{eqnarray*}
and
 \begin{eqnarray*} \mu_t(d{{z}}_0,\ldots,d{{z}}_t) &=& \prod_{j=k}^tK\bigg(\frac{d{{z}}_j -\psi_{j}^a({\boldsymbol{z}}_{j-k\,:\,j-1})}{\psi_j^b({\boldsymbol{z}}_{j-k\,:\,j-1})}\bigg)[G(d{{z}}_1\times\cdots\times d{{z}}_{k-1})]^{1(k>1)}\,H_0(d{{z}}_0)\end{eqnarray*}
\begin{eqnarray*} \mu_t(d{{z}}_0,\ldots,d{{z}}_t) &=& \prod_{j=k}^tK\bigg(\frac{d{{z}}_j -\psi_{j}^a({\boldsymbol{z}}_{j-k\,:\,j-1})}{\psi_j^b({\boldsymbol{z}}_{j-k\,:\,j-1})}\bigg)[G(d{{z}}_1\times\cdots\times d{{z}}_{k-1})]^{1(k>1)}\,H_0(d{{z}}_0)\end{eqnarray*}
on
![]() $[0,\infty)\times {{{\mathbb{R}}}}^t$
, where
$[0,\infty)\times {{{\mathbb{R}}}}^t$
, where
![]() $1(k>1)$
denotes the indicator function of
$1(k>1)$
denotes the indicator function of
![]() $\{k>1\}$
. For
$\{k>1\}$
. For
![]() $f\in C_b([0,\infty)\times {{{\mathbb{R}}}}^t)$
, we may write
$f\in C_b([0,\infty)\times {{{\mathbb{R}}}}^t)$
, we may write
 \begin{align*} & \mathbb{E}\,\bigg[f\bigg(\frac{X_0-u}{\sigma(u)},\frac{X_1-a_1(X_0)}{b_1(X_0)},\ldots,\frac{X_t-a_t(X_0)}{b_t(X_0)}\bigg)\,\bigg|\, X_0>u\bigg]=\\\\& =\int_{[0,\infty)\times {{{\mathbb{R}}}}^t} f({\boldsymbol{z}}_{0\,:\,t}) \mu_t^{(u)} (d{{z}}_0,\ldots,d{{z}}_t) \end{align*}
\begin{align*} & \mathbb{E}\,\bigg[f\bigg(\frac{X_0-u}{\sigma(u)},\frac{X_1-a_1(X_0)}{b_1(X_0)},\ldots,\frac{X_t-a_t(X_0)}{b_t(X_0)}\bigg)\,\bigg|\, X_0>u\bigg]=\\\\& =\int_{[0,\infty)\times {{{\mathbb{R}}}}^t} f({\boldsymbol{z}}_{0\,:\,t}) \mu_t^{(u)} (d{{z}}_0,\ldots,d{{z}}_t) \end{align*}
and
We need to show that
![]() $\mu_t^{(u)}$
converges weakly to
$\mu_t^{(u)}$
converges weakly to
![]() $\mu_t$
. Let
$\mu_t$
. Let
![]() $g_0\in C_b([0,\infty))$
and
$g_0\in C_b([0,\infty))$
and
![]() $g\in C_b({{{\mathbb{R}}}}^{k})$
. The proof is by induction on t. For
$g\in C_b({{{\mathbb{R}}}}^{k})$
. The proof is by induction on t. For
![]() $t = k$
it suffices to show that
$t = k$
it suffices to show that
 \begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{k}} g_0({{z}}_0) g({{z}}_1,\ldots,{{z}}_{k}) \mu_k^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{k})\nonumber\\\nonumber\\ &&= \int_{[0,\infty) } g_0({{z}}_0) \bigg[\int_{{{{\mathbb{R}}}}^{k}} g({\boldsymbol{z}}_{1\,:\,k}) \pi((v_u({{z}}_0),{\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),{\boldsymbol{z}}_{1\,:\,k-1})),A_{k}(v_u({{z}}_0),d{{z}}_k)) \nonumber\\\nonumber\\ && \qquad \qquad \qquad\qquad \pi_0( v_u({{z}}_0), {\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))^{{1(k>1)}}\bigg] \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)}\end{eqnarray}
\begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{k}} g_0({{z}}_0) g({{z}}_1,\ldots,{{z}}_{k}) \mu_k^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{k})\nonumber\\\nonumber\\ &&= \int_{[0,\infty) } g_0({{z}}_0) \bigg[\int_{{{{\mathbb{R}}}}^{k}} g({\boldsymbol{z}}_{1\,:\,k}) \pi((v_u({{z}}_0),{\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),{\boldsymbol{z}}_{1\,:\,k-1})),A_{k}(v_u({{z}}_0),d{{z}}_k)) \nonumber\\\nonumber\\ && \qquad \qquad \qquad\qquad \pi_0( v_u({{z}}_0), {\boldsymbol{A}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))^{{1(k>1)}}\bigg] \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)}\end{eqnarray}
converges to
![]() $\mathbb{E}(g_0(E_0))\,\mathbb{E}(g({{Z}}_1,\ldots,{{Z}}_k))$
.
$\mathbb{E}(g_0(E_0))\,\mathbb{E}(g({{Z}}_1,\ldots,{{Z}}_k))$
.
By Assumptions 2 and 3, the integrand in the term in square brackets in (50) converges pointwise to a limit and is dominated by
Lebesgue’s dominated convergence theorem yields that the term in square brackets in (50) is bounded and converges to
![]() $\mathbb{E}[g({\boldsymbol{Z}}_{1\,:\,k})]$
for
$\mathbb{E}[g({\boldsymbol{Z}}_{1\,:\,k})]$
for
![]() $u\to\infty$
, since
$u\to\infty$
, since
![]() $v_u({{z}}_0)\to \infty$
as
$v_u({{z}}_0)\to \infty$
as
![]() $u\to \infty$
. The convergence holds uniformly in the variable
$u\to \infty$
. The convergence holds uniformly in the variable
![]() ${{z}}_0\in[0,\infty)$
since
${{z}}_0\in[0,\infty)$
since
![]() $\sigma(u)>0$
. Therefore Lemma 3 applies, which guarantees convergence of the entire term (50) to
$\sigma(u)>0$
. Therefore Lemma 3 applies, which guarantees convergence of the entire term (50) to
![]() $\mathbb{E}(E_0)\,\mathbb{E}(g({\boldsymbol{Z}}_{1\,:\,k}))$
by Assumption 1.
$\mathbb{E}(E_0)\,\mathbb{E}(g({\boldsymbol{Z}}_{1\,:\,k}))$
by Assumption 1.
Next, assume that the statement is true for some
![]() $t > k$
. It suffices to show that for any
$t > k$
. It suffices to show that for any
![]() $g_0\in C_b([0,\infty)\times {{{\mathbb{R}}}}^t$
,
$g_0\in C_b([0,\infty)\times {{{\mathbb{R}}}}^t$
,
![]() $g\in C_b({{{\mathbb{R}}}})$
,
$g\in C_b({{{\mathbb{R}}}})$
,
 \begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t+1})\nonumber\\\nonumber\\ &&= \int_{[0,\infty)\times{{{\mathbb{R}}}}^t } g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{{{{\mathbb{R}}}}} g({{z}}_{t+1})\pi({\boldsymbol{A}}_{t-k+1\,:\,t}(v_u({{z}}_0),{\boldsymbol{z}}_{t-k+1\,:\,t}),A_t(v_u({{z}}_0),d{{z}}_{t+1})) \bigg]\nonumber\\\nonumber\\ &&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \mu_{t}^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t})\end{eqnarray}
\begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t+1})\nonumber\\\nonumber\\ &&= \int_{[0,\infty)\times{{{\mathbb{R}}}}^t } g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{{{{\mathbb{R}}}}} g({{z}}_{t+1})\pi({\boldsymbol{A}}_{t-k+1\,:\,t}(v_u({{z}}_0),{\boldsymbol{z}}_{t-k+1\,:\,t}),A_t(v_u({{z}}_0),d{{z}}_{t+1})) \bigg]\nonumber\\\nonumber\\ &&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \mu_{t}^{(u)}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t})\end{eqnarray}
converges to
 \begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t+1})\nonumber\\\nonumber\\ &&=\int_{[0,\infty)\times {{{\mathbb{R}}}}^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{{{{\mathbb{R}}}}}g({{z}}_{t+1})K\bigg(\frac{d{{z}}_{t+1} - \psi^a_{t}({\boldsymbol{z}}_{t-k+1\,:\,t})} {\psi^b_{t}({\boldsymbol{z}}_{t-k+1\,:\,t})}\bigg)\bigg] \mu_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t}).\nonumber\\\nonumber\\\end{eqnarray}
\begin{eqnarray} && \int_{[0,\infty)\times {{{\mathbb{R}}}}^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t+1})\nonumber\\\nonumber\\ &&=\int_{[0,\infty)\times {{{\mathbb{R}}}}^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{{{{\mathbb{R}}}}}g({{z}}_{t+1})K\bigg(\frac{d{{z}}_{t+1} - \psi^a_{t}({\boldsymbol{z}}_{t-k+1\,:\,t})} {\psi^b_{t}({\boldsymbol{z}}_{t-k+1\,:\,t})}\bigg)\bigg] \mu_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_{t}).\nonumber\\\nonumber\\\end{eqnarray}
The term in square brackets in (51) is bounded, and by Lemma 1 and Assumptions 2 and 3, it converges uniformly on compact sets in both variables
![]() $({{z}}_0,{\boldsymbol{z}}_{t-k+1\,:\,t})\in[0,\infty)\times {{{\mathbb{R}}}}^k$
jointly, since
$({{z}}_0,{\boldsymbol{z}}_{t-k+1\,:\,t})\in[0,\infty)\times {{{\mathbb{R}}}}^k$
jointly, since
![]() $\sigma(u)>0$
. Hence the induction hypothesis and Lemma 3 imply the desired result.
$\sigma(u)>0$
. Hence the induction hypothesis and Lemma 3 imply the desired result.
Proof of Theorem 2. Define
Consider the measures
 \begin{align} \mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t) & = \bigg[\prod_{j=k}^t \pi({\boldsymbol{b}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-k\,:\,j-1}),b_j(v_u({{z}}_0)) \,d{{z}}_j)\bigg]\nonumber \\ \nonumber\\ & \times [\pi_0( v_u({{z}}_0), {\boldsymbol{b}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))]^{1(k>1)} \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{align}
\begin{align} \mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t) & = \bigg[\prod_{j=k}^t \pi({\boldsymbol{b}}_{j-k\,:\,j-1}(v_u({{z}}_0),{\boldsymbol{z}}_{j-k\,:\,j-1}),b_j(v_u({{z}}_0)) \,d{{z}}_j)\bigg]\nonumber \\ \nonumber\\ & \times [\pi_0( v_u({{z}}_0), {\boldsymbol{b}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1}))]^{1(k>1)} \frac{F_0( v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{align}
and
 \begin{eqnarray} \mu_t(d{{z}}_0,\ldots,d{{z}}_t)&=& \bigg[\prod_{j=k}^t K\bigg(\frac{d{{z}}_j}{\psi^b_{j}({\boldsymbol{z}}_{j-k\,:\,j-1})}\bigg)\bigg] [G(d{{z}}_1, \ldots, d{{z}}_{k-1})]^{1(k>1)} H_0(d{{z}}_0) \end{eqnarray}
\begin{eqnarray} \mu_t(d{{z}}_0,\ldots,d{{z}}_t)&=& \bigg[\prod_{j=k}^t K\bigg(\frac{d{{z}}_j}{\psi^b_{j}({\boldsymbol{z}}_{j-k\,:\,j-1})}\bigg)\bigg] [G(d{{z}}_1, \ldots, d{{z}}_{k-1})]^{1(k>1)} H_0(d{{z}}_0) \end{eqnarray}
on
![]() $[0,\infty) \times [0,\infty)^t$
. We may write
$[0,\infty) \times [0,\infty)^t$
. We may write
and
for
![]() $f \in C_b([0,\infty)\times [0,\infty)^t)$
. Note that
$f \in C_b([0,\infty)\times [0,\infty)^t)$
. Note that
![]() $b_j(0)$
,
$b_j(0)$
,
![]() $j=1,\ldots,t$
, need not be defined in (53), since
$j=1,\ldots,t$
, need not be defined in (53), since
![]() $v_u({{z}}_0)\geq u>0$
for
$v_u({{z}}_0)\geq u>0$
for
![]() ${{z}}_0\geq 0$
and sufficiently large u, whereas (54) is well-defined, since the measures G and K put no mass at any half-plane
${{z}}_0\geq 0$
and sufficiently large u, whereas (54) is well-defined, since the measures G and K put no mass at any half-plane
![]() $C_j=\{({\boldsymbol{z}}_{1\,:\,k-1})\in [0,\infty)^{k-1}: {{{z}}_j = 0}\}\in [0,\infty)^{k-1}$
and at
$C_j=\{({\boldsymbol{z}}_{1\,:\,k-1})\in [0,\infty)^{k-1}: {{{z}}_j = 0}\}\in [0,\infty)^{k-1}$
and at
![]() $0\in [0,\infty)$
, respectively. Formally, we may set
$0\in [0,\infty)$
, respectively. Formally, we may set
![]() $\psi^b_{j}({\textbf{0}}_k)=1$
,
$\psi^b_{j}({\textbf{0}}_k)=1$
,
![]() $j=1,\ldots,t$
, in order to emphasize that we consider measures on
$j=1,\ldots,t$
, in order to emphasize that we consider measures on
![]() $[0,\infty)^{t+1}$
instead of
$[0,\infty)^{t+1}$
instead of
![]() $[0,\infty)\times (0,\infty)^t$
. To prove the theorem, we need to show that
$[0,\infty)\times (0,\infty)^t$
. To prove the theorem, we need to show that
![]() $\mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t)$
converges weakly to
$\mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t)$
converges weakly to
![]() $\mu_t(d{{z}}_0,\ldots,d{{z}}_t)$
. The proof is by induction on t. We show two statements by induction on t:
$\mu_t(d{{z}}_0,\ldots,d{{z}}_t)$
. The proof is by induction on t. We show two statements by induction on t:
(I)
![]() $\mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t)$
converges weakly to
$\mu^{(u)}_t(d{{z}}_0,\ldots,d{{z}}_t)$
converges weakly to
![]() $\mu_t(d{{z}}_0,\ldots,d{{z}}_t)$
as
$\mu_t(d{{z}}_0,\ldots,d{{z}}_t)$
as
![]() $u \uparrow \infty$
;
$u \uparrow \infty$
;
(II) for all
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $\delta_t>0$
such that
$\delta_t>0$
such that
![]() $\mu_t([0,\infty)\times [0,\infty)^{t-1} \times[0,\delta_t])<{{\varepsilon}}$
.
$\mu_t([0,\infty)\times [0,\infty)^{t-1} \times[0,\delta_t])<{{\varepsilon}}$
.
We start by proving the case
![]() $t=k$
.
$t=k$
.
(I)
![]() $\underline{\mathrm{for}\ t=k}$
: It suffices to show that for any
$\underline{\mathrm{for}\ t=k}$
: It suffices to show that for any
![]() $g_0 \in C_b([0,\infty))$
and
$g_0 \in C_b([0,\infty))$
and
![]() $g \in C_b([0,\infty)^{k-1})$
,
$g \in C_b([0,\infty)^{k-1})$
,
 \begin{align} \notag&\int_{[0,\infty)\times [0,\infty)^{k-1} \times [0,\infty)} g_0({{z}}_0) g({\boldsymbol{z}}_{1\,:\,k}) \mu^{(u)}_1(d{{z}}_0,\ldots, d{{z}}_k)\\ \notag=&\int_{[0,\infty)} g_0({{z}}_0) \\ \notag & \times\bigg[\int_{[0,\infty)^{k-1}} \int_{[0,\infty)} g({{z}}_1,\ldots,{{z}}_{k}) \pi((v_u({{z}}_0),{\boldsymbol{b}}_{0\,:\,k-1}(v_u({{z}}_0),{\boldsymbol{z}}_{0\,:\,k-1})),b_{k}(v_u({{z}}_0))d{{z}}_k)\bigg]\nonumber \\ & \qquad \qquad \qquad \times \pi_0( v_u({{z}}_0), {\boldsymbol{b}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1})) \frac{F_0(v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{align}
\begin{align} \notag&\int_{[0,\infty)\times [0,\infty)^{k-1} \times [0,\infty)} g_0({{z}}_0) g({\boldsymbol{z}}_{1\,:\,k}) \mu^{(u)}_1(d{{z}}_0,\ldots, d{{z}}_k)\\ \notag=&\int_{[0,\infty)} g_0({{z}}_0) \\ \notag & \times\bigg[\int_{[0,\infty)^{k-1}} \int_{[0,\infty)} g({{z}}_1,\ldots,{{z}}_{k}) \pi((v_u({{z}}_0),{\boldsymbol{b}}_{0\,:\,k-1}(v_u({{z}}_0),{\boldsymbol{z}}_{0\,:\,k-1})),b_{k}(v_u({{z}}_0))d{{z}}_k)\bigg]\nonumber \\ & \qquad \qquad \qquad \times \pi_0( v_u({{z}}_0), {\boldsymbol{b}}_{1\,:\,k-1}(v_u({{z}}_0),d{\boldsymbol{z}}_{1\,:\,k-1})) \frac{F_0(v_u(d{{z}}_0))}{\overline{F}_0(u)} \end{align}
converges to
By Assumptions 1 and 5, the integrand in the term in square brackets converges pointwise to a limit and is dominated by
Lebesgue’s dominated convergence theorem yields that the term in square brackets in (55) is bounded and converges to
![]() ${{\mathbb{E}}}(g({\boldsymbol{Z}}_{1\,:\,k}))$
for
${{\mathbb{E}}}(g({\boldsymbol{Z}}_{1\,:\,k}))$
for
![]() $u\uparrow \infty$
, since
$u\uparrow \infty$
, since
![]() $v_u({{z}}_0) \to \infty$
for
$v_u({{z}}_0) \to \infty$
for
![]() $u \uparrow \infty$
. The convergence is uniform in the variable
$u \uparrow \infty$
. The convergence is uniform in the variable
![]() ${{z}}_0$
, since
${{z}}_0$
, since
![]() $\sigma(u)>0$
. Therefore, Lemma 3(i) applies, which guarantees convergence of the entire term (55) to
$\sigma(u)>0$
. Therefore, Lemma 3(i) applies, which guarantees convergence of the entire term (55) to
![]() ${{\mathbb{E}}}(g_0(E_0)) {{\mathbb{E}}}[g({\boldsymbol{Z}}_{1\,:\,k})]$
by Assumption 1.
${{\mathbb{E}}}(g_0(E_0)) {{\mathbb{E}}}[g({\boldsymbol{Z}}_{1\,:\,k})]$
by Assumption 1.
(II)
![]() $\underline{\mathrm{for}\ t=k}$
: Since
$\underline{\mathrm{for}\ t=k}$
: Since
![]() $K(\{0\})=0$
, there exists
$K(\{0\})=0$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $K([0,\delta])<{{\varepsilon}}$
, which immediately implies
$K([0,\delta])<{{\varepsilon}}$
, which immediately implies
![]() $\mu_k([0,\infty)^{k}\times[0,\delta])=H_0([0,\infty))\,\smash{[G([0,\infty)^{k-1})]^{ 1(k>1) }}\,K([0,\delta])<\varepsilon$
.
$\mu_k([0,\infty)^{k}\times[0,\delta])=H_0([0,\infty))\,\smash{[G([0,\infty)^{k-1})]^{ 1(k>1) }}\,K([0,\delta])<\varepsilon$
.
Now, let us assume that both statements ((I) and (II)) are proved for some
![]() $t \in {{\mathbb{N}}}$
.
$t \in {{\mathbb{N}}}$
.
![]() $\underline{\mathrm{(I) for}\ t+1}$
: It suffices to show that for any
$\underline{\mathrm{(I) for}\ t+1}$
: It suffices to show that for any
![]() $g_0 \in C_b([0,\infty)\times [0,\infty)^t)$
,
$g_0 \in C_b([0,\infty)\times [0,\infty)^t)$
,
![]() $g\in C_b([0,\infty))$
,
$g\in C_b([0,\infty))$
,
 \begin{align} \notag &\int_{[0,\infty)\times [0,\infty)^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) \times g({{z}}_{t+1}) \mu^{(u)}_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t,d{{z}}_{t+1})\\ \notag =&\int_{[0,\infty)\times [0,\infty)^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \\ &\times\bigg[\int_{[0,\infty)} g({{z}}_{t+1}) \pi({\boldsymbol{b}}_{t-k+1\,:\,t}(v_u({{z}}_0), {\boldsymbol{z}}_{t-k+1\,:\,t}), b_{t+1}(v_u({{z}}_0))\,d{{z}}_{t+1})\bigg]\nonumber\\&\times\mu^{(u)}_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t) \end{align}
\begin{align} \notag &\int_{[0,\infty)\times [0,\infty)^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) \times g({{z}}_{t+1}) \mu^{(u)}_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t,d{{z}}_{t+1})\\ \notag =&\int_{[0,\infty)\times [0,\infty)^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \\ &\times\bigg[\int_{[0,\infty)} g({{z}}_{t+1}) \pi({\boldsymbol{b}}_{t-k+1\,:\,t}(v_u({{z}}_0), {\boldsymbol{z}}_{t-k+1\,:\,t}), b_{t+1}(v_u({{z}}_0))\,d{{z}}_{t+1})\bigg]\nonumber\\&\times\mu^{(u)}_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t) \end{align}
converges to
 \begin{eqnarray} \notag&\int_{[0,\infty)\times [0,\infty)^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t,d{{z}}_{t+1})\\ &=\int_{[0,\infty)\times [0,\infty)^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{[0,\infty)}g({{z}}_{t+1}) K\big(d{{z}}_{t+1}/\psi_{{{t}}}^b\big({\boldsymbol{z}}_{t-k+1\,:\,t}\big)\big) \bigg]\nonumber\\ &\hspace{3cm}\times \mu_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t). \end{eqnarray}
\begin{eqnarray} \notag&\int_{[0,\infty)\times [0,\infty)^{t+1}} g_0({\boldsymbol{z}}_{0\,:\,t}) g({{z}}_{t+1}) \mu_{t+1}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t,d{{z}}_{t+1})\\ &=\int_{[0,\infty)\times [0,\infty)^{t}} g_0({\boldsymbol{z}}_{0\,:\,t}) \bigg[\int_{[0,\infty)}g({{z}}_{t+1}) K\big(d{{z}}_{t+1}/\psi_{{{t}}}^b\big({\boldsymbol{z}}_{t-k+1\,:\,t}\big)\big) \bigg]\nonumber\\ &\hspace{3cm}\times \mu_{t}(d{{z}}_0,d{{z}}_1,\ldots,d{{z}}_t). \end{eqnarray}
From Lemma 2 and Assumptions 4 and 5 we know that, for any
![]() $\delta>0$
, the (bounded) term in square brackets in (56) converges uniformly on compact sets in the variable
$\delta>0$
, the (bounded) term in square brackets in (56) converges uniformly on compact sets in the variable
![]() ${\boldsymbol{z}}_{t-k+1\,:\,t} \in \prod_{i=1}^k[\delta_i,\infty)$
to the continuous function
${\boldsymbol{z}}_{t-k+1\,:\,t} \in \prod_{i=1}^k[\delta_i,\infty)$
to the continuous function
(the term in square brackets in (57)). This convergence holds even uniformly on compact sets in both variables
![]() $({{z}}_0,{\boldsymbol{z}}_{t-k+1\,:\,t}) \in [0,\infty)\times \prod_{i=1}^k[\delta_i,\infty)$
jointly, since
$({{z}}_0,{\boldsymbol{z}}_{t-k+1\,:\,t}) \in [0,\infty)\times \prod_{i=1}^k[\delta_i,\infty)$
jointly, since
![]() $\sigma(u)>0$
. Hence, the induction hypothesis (I) and Lemma 3(i) imply that for any
$\sigma(u)>0$
. Hence, the induction hypothesis (I) and Lemma 3(i) imply that for any
![]() $\delta>0$
the integral in (56) converges to the integral in (57) if the integrals with respect to
$\delta>0$
the integral in (56) converges to the integral in (57) if the integrals with respect to
![]() $\mu_t$
and
$\mu_t$
and
![]() $\mu_t^{(u)}$
were restricted to
$\mu_t^{(u)}$
were restricted to
![]() $A_\delta\,:\!=\,[0,\infty)\times [0,\infty)^{t-1} \times [\delta,\infty)$
(instead of being taken over
$A_\delta\,:\!=\,[0,\infty)\times [0,\infty)^{t-1} \times [\delta,\infty)$
(instead of being taken over
![]() $[0,\infty)\times [0,\infty)^{t-1} \times [0,\infty)$
).
$[0,\infty)\times [0,\infty)^{t-1} \times [0,\infty)$
).
Since
![]() $g_0$
and g are bounded, it suffices to control the mass of
$g_0$
and g are bounded, it suffices to control the mass of
![]() $\mu_t$
and
$\mu_t$
and
![]() $\mu_t^{(u)}$
on the complement
$\mu_t^{(u)}$
on the complement
![]() $A_\delta^c=[0,\infty)\times [0,\infty)^{t-1} \times [0,\delta)$
. For some prescribed
$A_\delta^c=[0,\infty)\times [0,\infty)^{t-1} \times [0,\delta)$
. For some prescribed
![]() ${{\varepsilon}}>0$
it is possible to find some sufficiently small
${{\varepsilon}}>0$
it is possible to find some sufficiently small
![]() $\delta>0$
and sufficiently large u so that
$\delta>0$
and sufficiently large u so that
![]() $\mu_t(A_\delta^c)<{{\varepsilon}}$
and
$\mu_t(A_\delta^c)<{{\varepsilon}}$
and
![]() $\mu^{(u)}_t(A^c_\delta)<2{{\varepsilon}}$
. Because of the induction hypothesis (II), we indeed have
$\mu^{(u)}_t(A^c_\delta)<2{{\varepsilon}}$
. Because of the induction hypothesis (II), we indeed have
![]() $\mu_t(A_{\delta_t})<{{\varepsilon}}$
for some
$\mu_t(A_{\delta_t})<{{\varepsilon}}$
for some
![]() $\delta_t>0$
. Choose
$\delta_t>0$
. Choose
![]() $\delta=\delta_t/2$
and note that the sets of the form
$\delta=\delta_t/2$
and note that the sets of the form
![]() $A_\delta$
are nested. Let
$A_\delta$
are nested. Let
![]() $C_\delta$
be a continuity set of
$C_\delta$
be a continuity set of
![]() $\mu_t$
with
$\mu_t$
with
![]() $A^c_\delta\subset C_\delta \subset A^c_{2\delta}$
. Then the value of
$A^c_\delta\subset C_\delta \subset A^c_{2\delta}$
. Then the value of
![]() $\mu_t$
on all three sets
$\mu_t$
on all three sets
![]() $A^c_\delta,C_\delta,A^c_{2\delta}$
is smaller than
$A^c_\delta,C_\delta,A^c_{2\delta}$
is smaller than
![]() ${{\varepsilon}}$
, and by the induction hypothesis (I), the value
${{\varepsilon}}$
, and by the induction hypothesis (I), the value
![]() $\mu^{(u)}_t(C_\delta)$
converges to
$\mu^{(u)}_t(C_\delta)$
converges to
![]() $\mu_t(C_\delta)<{{\varepsilon}}$
. Hence, for sufficiently large u, we also have
$\mu_t(C_\delta)<{{\varepsilon}}$
. Hence, for sufficiently large u, we also have
![]() $\mu^{(u)}_t(A^c_\delta)<\mu^{(u)}_{t}(C_\delta)<\mu_t(C_\delta)+{{\varepsilon}}<2{{\varepsilon}}$
, as desired.
$\mu^{(u)}_t(A^c_\delta)<\mu^{(u)}_{t}(C_\delta)<\mu_t(C_\delta)+{{\varepsilon}}<2{{\varepsilon}}$
, as desired.
![]() $\underline{\mathrm{(II) for}\ t+1}$
: We have for any
$\underline{\mathrm{(II) for}\ t+1}$
: We have for any
![]() $\delta>0$
and any
$\delta>0$
and any
![]() $c>0$
$c>0$
Splitting the integral according to
![]() $\big\{\psi_{{{t}}}^b({\boldsymbol{z}}_{t-k+1\,:\,t})>c\big\}$
or
$\big\{\psi_{{{t}}}^b({\boldsymbol{z}}_{t-k+1\,:\,t})>c\big\}$
or
![]() $\big\{\psi_{{{t}}}^b({\boldsymbol{z}}_{t-k+1\,:\,t})\leq c\big\}$
yields
$\big\{\psi_{{{t}}}^b({\boldsymbol{z}}_{t-k+1\,:\,t})\leq c\big\}$
yields
By Assumption 5(i) and the induction hypothesis (II), we may choose
![]() $c>0$
sufficiently small so that the second summand
$c>0$
sufficiently small so that the second summand
![]() $\mu_t([0,\infty)\times [0,\infty)^{t-1}\times(\psi_{{{t}}}^b)^{-1}([0,c])\})$
is smaller than
$\mu_t([0,\infty)\times [0,\infty)^{t-1}\times(\psi_{{{t}}}^b)^{-1}([0,c])\})$
is smaller than
![]() ${{\varepsilon}}/2$
. Next, since
${{\varepsilon}}/2$
. Next, since
![]() $K(\{0\})=0$
, it is possible to choose
$K(\{0\})=0$
, it is possible to choose
![]() $\delta_{t+1}=\delta>0$
accordingly small so that the first summand
$\delta_{t+1}=\delta>0$
accordingly small so that the first summand
![]() $K\big(\big[0,\frac{\delta}{c}\big]\big)$
is smaller than
$K\big(\big[0,\frac{\delta}{c}\big]\big)$
is smaller than
![]() ${{\varepsilon}}/2$
, which shows (II) for
${{\varepsilon}}/2$
, which shows (II) for
![]() $t+1$
.
$t+1$
.
A.3. Proofs of Propositions
Proof of Proposition 1. We start by proving that (i) implies (ii). Let
![]() ${\textbf{0}} \,:\!=\, {\textbf{0}}_k$
and suppose there exist
${\textbf{0}} \,:\!=\, {\textbf{0}}_k$
and suppose there exist
![]() $a_t$
,
$a_t$
,
![]() $b_t$
,
$b_t$
,
![]() $\psi_t^a$
, and
$\psi_t^a$
, and
![]() $\psi_t^b$
such that (i) holds. Then, for
$\psi_t^b$
such that (i) holds. Then, for
![]() $t=k,k+1\ldots$
,
$t=k,k+1\ldots$
,
 \begin{align*} & \frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))}{b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))} \\\\& =\frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a_t({{v}})}{b_t({{v}})}\frac{b_t({{v}})}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))} -\frac{a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))-a_t({{v}})}{b_t({{v}})}\frac{b_t({{v}})}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))}\\\\& \to \frac{\psi_t^a({\boldsymbol{z}})}{\psi_t^b({\textbf{0}})} - \frac{\psi_t^a({\textbf{0}})}{\psi_t^b({\textbf{0}})} = \frac{\psi_t^a({\boldsymbol{z}}) - \psi_t^a({\textbf{0}})}{\psi_t^b({\textbf{0}})} \quad \text{whenever ${\boldsymbol{z}}_{{v}} \to {\boldsymbol{z}}$ as $v\to\infty$},\end{align*}
\begin{align*} & \frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))}{b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))} \\\\& =\frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a_t({{v}})}{b_t({{v}})}\frac{b_t({{v}})}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))} -\frac{a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))-a_t({{v}})}{b_t({{v}})}\frac{b_t({{v}})}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))}\\\\& \to \frac{\psi_t^a({\boldsymbol{z}})}{\psi_t^b({\textbf{0}})} - \frac{\psi_t^a({\textbf{0}})}{\psi_t^b({\textbf{0}})} = \frac{\psi_t^a({\boldsymbol{z}}) - \psi_t^a({\textbf{0}})}{\psi_t^b({\textbf{0}})} \quad \text{whenever ${\boldsymbol{z}}_{{v}} \to {\boldsymbol{z}}$ as $v\to\infty$},\end{align*}
and
Next we prove (ii) implies (i). Let
![]() $a_t({{v}}) = a({\boldsymbol{A}}_t({{v}}, 0)) - c\,b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))$
and
$a_t({{v}}) = a({\boldsymbol{A}}_t({{v}}, 0)) - c\,b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))$
and
![]() $b_t({{v}})=d\, b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))$
for arbitrary constants
$b_t({{v}})=d\, b({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))$
for arbitrary constants
![]() $c\in {{{\mathbb{R}}}}$
,
$c\in {{{\mathbb{R}}}}$
,
![]() $d\in {{{\mathbb{R}}}}_+$
. Then, for
$d\in {{{\mathbb{R}}}}_+$
. Then, for
![]() $t=k,k+1\ldots$
,
$t=k,k+1\ldots$
,
 \begin{eqnarray*} \frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a_t({{v}})}{b_t({{v}})} &=& \frac{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))}{b_t({{v}})} \bigg[\frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))} + c\bigg]\\ &\to& \frac{\lambda_t^b({\boldsymbol{z}})}{d}[\lambda_t^a({\boldsymbol{z}})+c] \quad \text{whenever ${\boldsymbol{z}}_{{v}}\to{\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$ as ${{v}}\to\infty$.}\end{eqnarray*}
\begin{eqnarray*} \frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a_t({{v}})}{b_t({{v}})} &=& \frac{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))}{b_t({{v}})} \bigg[\frac{a({\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{{v}}))-a({\boldsymbol{A}}_t({{v}}, {\textbf{0}}))}{b({\boldsymbol{A}}_t({{v}},{\textbf{0}}))} + c\bigg]\\ &\to& \frac{\lambda_t^b({\boldsymbol{z}})}{d}[\lambda_t^a({\boldsymbol{z}})+c] \quad \text{whenever ${\boldsymbol{z}}_{{v}}\to{\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$ as ${{v}}\to\infty$.}\end{eqnarray*}
Define
![]() $\psi_t^a({\boldsymbol{z}}) = (\lambda_t^a({\boldsymbol{z}}) + c)/d$
and
$\psi_t^a({\boldsymbol{z}}) = (\lambda_t^a({\boldsymbol{z}}) + c)/d$
and
![]() $\psi_t^b({\boldsymbol{z}})=\lambda_t^b({\boldsymbol{z}})/d$
. By assumption,
$\psi_t^b({\boldsymbol{z}})=\lambda_t^b({\boldsymbol{z}})/d$
. By assumption,
![]() $\lambda_t^a({\textbf{0}})=0$
and
$\lambda_t^a({\textbf{0}})=0$
and
![]() $\lambda_t^b({\textbf{0}}) = 1$
. Hence,
$\lambda_t^b({\textbf{0}}) = 1$
. Hence,
![]() $\lambda_t^a({\boldsymbol{z}}) = [\psi_t^a({\boldsymbol{z}}) - \psi_t^a({\textbf{0}})]/\psi_t^b({\textbf{0}})$
and
$\lambda_t^a({\boldsymbol{z}}) = [\psi_t^a({\boldsymbol{z}}) - \psi_t^a({\textbf{0}})]/\psi_t^b({\textbf{0}})$
and
![]() $\lambda_t^b({\boldsymbol{z}})=\psi_t^b({\boldsymbol{z}})/\psi_t^b({\textbf{0}})$
, which completes the proof.
$\lambda_t^b({\boldsymbol{z}})=\psi_t^b({\boldsymbol{z}})/\psi_t^b({\textbf{0}})$
, which completes the proof.
Proof of Proposition 2. The recurrence relation
 \begin{align*} \alpha_t = c \, \bigg[\sum_{i=1}^k \gamma_i (\gamma_i\, \alpha_{t-k+i-1})^\delta/\big(\gamma_1^{1+\delta} + \cdots + \gamma_k^{1+\delta}\big) \bigg]^{1/\delta} \end{align*}
\begin{align*} \alpha_t = c \, \bigg[\sum_{i=1}^k \gamma_i (\gamma_i\, \alpha_{t-k+i-1})^\delta/\big(\gamma_1^{1+\delta} + \cdots + \gamma_k^{1+\delta}\big) \bigg]^{1/\delta} \end{align*}
can be converted to the homogeneous linear recurrence relation
![]() $y_t = \sum_{i=1}^k c_i \, y_{t-k+i-1}$
, where
$y_t = \sum_{i=1}^k c_i \, y_{t-k+i-1}$
, where
![]() $\{y_t\} = \big\{\alpha_{t}^{\delta}\big\}$
and
$\{y_t\} = \big\{\alpha_{t}^{\delta}\big\}$
and
![]() $c_i=c^\delta \gamma_i^{1+\delta}/\big(\gamma_1^{1+\delta} + \cdots + \gamma_k^{1+\delta}\big)$
. Solving the recurrence relation and transforming the solution to the original sequence
$c_i=c^\delta \gamma_i^{1+\delta}/\big(\gamma_1^{1+\delta} + \cdots + \gamma_k^{1+\delta}\big)$
. Solving the recurrence relation and transforming the solution to the original sequence
![]() $\{\alpha_t\}$
leads to the claim.
$\{\alpha_t\}$
leads to the claim.
Proof of Proposition 3. (i) Because
![]() $a_P$
is 1-homogeneous, a satisfies the property (19). By the definition of the right-inverse
$a_P$
is 1-homogeneous, a satisfies the property (19). By the definition of the right-inverse
![]() $V_{0\,:\,k-1}^{\leftarrow}$
and Assumption 8, we have that, for all
$V_{0\,:\,k-1}^{\leftarrow}$
and Assumption 8, we have that, for all
![]() $({\boldsymbol{y}}_{0\,:\,k-1},q)$
in the domain of
$({\boldsymbol{y}}_{0\,:\,k-1},q)$
in the domain of
![]() $V_{0\,:\,k-1}^\leftarrow$
,
$V_{0\,:\,k-1}^\leftarrow$
,
Hence
![]() $V_{0\,:\,k-1}^{\leftarrow}(q;{\boldsymbol{y}}_{0\,:\,k-1}) = a_P({\boldsymbol{y}}_{0\,:\,k-1})\, K_P^{\leftarrow}\big\{q/V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1},\infty)\big\}$
. Taking logarithms, setting
$V_{0\,:\,k-1}^{\leftarrow}(q;{\boldsymbol{y}}_{0\,:\,k-1}) = a_P({\boldsymbol{y}}_{0\,:\,k-1})\, K_P^{\leftarrow}\big\{q/V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1},\infty)\big\}$
. Taking logarithms, setting
![]() ${\boldsymbol{y}}_{0\,:\,k-1}=e^{{\boldsymbol{x}}_{0\,:\,k-1}}$
, and letting
${\boldsymbol{y}}_{0\,:\,k-1}=e^{{\boldsymbol{x}}_{0\,:\,k-1}}$
, and letting
![]() $q=p^\star\,V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1},\infty)$
where
$q=p^\star\,V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1},\infty)$
where
![]() $p^\star$
satisfies
$p^\star$
satisfies
![]() $K_P^\leftarrow(p^\star)=1$
gives
$K_P^\leftarrow(p^\star)=1$
gives
(ii) Since a satisfies the property (19), Appendix A.7 shows that Assumption 3 holds with limit distribution
![]() $K(x;{\boldsymbol{z}}_{0\,:\,k-1})$
given by (42). Using Assumption 8, we further have that under the normalizing functionals a and b, (42) simplifies to
$K(x;{\boldsymbol{z}}_{0\,:\,k-1})$
given by (42). Using Assumption 8, we further have that under the normalizing functionals a and b, (42) simplifies to
![]() $K(x;{\boldsymbol{z}}_{0\,:\,k-1})=K_P(e^x)$
for all
$K(x;{\boldsymbol{z}}_{0\,:\,k-1})=K_P(e^x)$
for all
![]() ${\boldsymbol{z}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
.
${\boldsymbol{z}}_{0\,:\,k-1}\in{{{\mathbb{R}}}}^k$
.
(iii) The limit distribution
![]() $K(x;{\boldsymbol{z}}_{0\,:\,k-1})$
in (42) does not depend on
$K(x;{\boldsymbol{z}}_{0\,:\,k-1})$
in (42) does not depend on
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
. Because
${\boldsymbol{z}}_{0\,:\,k-1}$
. Because
![]() $a_P$
is positive, 1-homogeneous, and continuous, 1 is in the image of
$a_P$
is positive, 1-homogeneous, and continuous, 1 is in the image of
![]() $a_P$
and thus 0 is in the image of a. Hence there exists
$a_P$
and thus 0 is in the image of a. Hence there exists
![]() ${\boldsymbol{z}}_{0\,:\,k-1}^\star\in{{{\mathbb{R}}}}^k$
such that
${\boldsymbol{z}}_{0\,:\,k-1}^\star\in{{{\mathbb{R}}}}^k$
such that
![]() $a({\boldsymbol{z}}_{0\,:\,k-1}^\star)=0$
and
$a({\boldsymbol{z}}_{0\,:\,k-1}^\star)=0$
and
![]() $K_P(e^x)=K(x;{\boldsymbol{z}}_{0\,:\,k-1}^\star)$
, which proves the claim.
$K_P(e^x)=K(x;{\boldsymbol{z}}_{0\,:\,k-1}^\star)$
, which proves the claim.
A.4. Proof of Corollaries
Proof of Corollary 1. Since a is continuous, we have that
![]() $a({{v}}{\textbf{1}}_k + {\boldsymbol{z}}_{{v}}) - {{v}} = a({\boldsymbol{z}}_{{v}})\to a({\boldsymbol{z}})$
whenever
$a({{v}}{\textbf{1}}_k + {\boldsymbol{z}}_{{v}}) - {{v}} = a({\boldsymbol{z}}_{{v}})\to a({\boldsymbol{z}})$
whenever
![]() ${\boldsymbol{z}}_{{v}}\to{\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
. Hence the convergence (8) holds true with
${\boldsymbol{z}}_{{v}}\to{\boldsymbol{z}}\in{{{\mathbb{R}}}}^k$
. Hence the convergence (8) holds true with
![]() $\psi_t^a({\boldsymbol{z}})=a({\boldsymbol{z}})$
and
$\psi_t^a({\boldsymbol{z}})=a({\boldsymbol{z}})$
and
![]() $\psi_t^b({\boldsymbol{z}})=1$
.
$\psi_t^b({\boldsymbol{z}})=1$
.
For any
![]() $s\in {{\mathbb{N}}}$
, [Reference Asenova and Segers1] show that under the assumptions of Corollary 1, the random vector
$s\in {{\mathbb{N}}}$
, [Reference Asenova and Segers1] show that under the assumptions of Corollary 1, the random vector
![]() ${\boldsymbol{X}}_{P}= \exp({\boldsymbol{X}}_{0\,:\, s})$
is multivariate regularly varying; that is, for any
${\boldsymbol{X}}_{P}= \exp({\boldsymbol{X}}_{0\,:\, s})$
is multivariate regularly varying; that is, for any
![]() $A\subset {{\Delta}}^{s}$
,
$A\subset {{\Delta}}^{s}$
,
where H is a Radon measure on
![]() ${{\Delta}}^{s}$
satisfying
${{\Delta}}^{s}$
satisfying
![]() $H({{\Delta}}^s)=s+1$
and
$H({{\Delta}}^s)=s+1$
and
![]() $\int_{{{\Delta}}^s} w_j dH({\boldsymbol{w}}_{0\,:\,s}) = 1$
for
$\int_{{{\Delta}}^s} w_j dH({\boldsymbol{w}}_{0\,:\,s}) = 1$
for
![]() $j=0,\ldots,s$
. Theorem 1 and Proposition 4 of [Reference Heffernan and Resnick8] imply that
$j=0,\ldots,s$
. Theorem 1 and Proposition 4 of [Reference Heffernan and Resnick8] imply that
![]() ${{Z}}_t\sim G_t$
where
${{Z}}_t\sim G_t$
where
Here
![]() $H_t$
denotes the lag-t bivariate spectral measure associated with H; that is, for every
$H_t$
denotes the lag-t bivariate spectral measure associated with H; that is, for every
![]() $t \geq 1$
,
$t \geq 1$
,
![]() $H_t$
is a Radon measure on
$H_t$
is a Radon measure on
![]() ${{\Delta}}^1$
that satisfies
${{\Delta}}^1$
that satisfies
![]() $H_t({{\Delta}}^1)=2$
and
$H_t({{\Delta}}^1)=2$
and
![]() $\int_{{{\Delta}}^1} w dH_t(w)=1$
. Thus, we have that the expected value of
$\int_{{{\Delta}}^1} w dH_t(w)=1$
. Thus, we have that the expected value of
![]() ${{Z}}_t$
satisfies
${{Z}}_t$
satisfies
 \begin{align*} & \mathbb{E}({{Z}}_t)=\int_{{{\mathbb{R}}}} z \,\mathrm{d}G_t(z)= \int_{{{\mathbb{R}}}} \int\limits_{0}^z \,\mathrm{d}u\, \,\mathrm{d}G_t(z) =-\int\limits_{-\infty}^0 G_t(z)\,\mathrm{d}{z} + \int\limits_{0}^{\infty} [1 - G_t(z)]\,\mathrm{d}{z}\\& =-\int\limits_{0}^{1/2} \int\limits_0^u (1-w)\,\mathrm{d} H_t(w)\,\mathrm{d}\log\Big(\frac{u}{1-u}\Big) + \int\limits_{1/2}^{1} \int\limits_u^1 (1-w)\,\mathrm{d} H_t(w)\,\mathrm{d}\log\Big(\frac{u}{1-u}\Big) \\ & =-\int\limits_{0}^{1/2} \int\limits_w^{1/2} \bigg[\mathrm{d}\log\Big(\frac{u}{1-u}\Big)\bigg]\, (1-w)\,\mathrm{d} H_t(w) + \int\limits_{1/2}^{1} \int\limits_{1/2}^w \bigg[\mathrm{d}\log\Big(\frac{u}{1-u}\Big)\bigg]\,(1-w)\,\mathrm{d} H_t(w) \\ & = \int_{{{\Delta}}^1} \log\{w/(1-w)\}\, (1-w)\,\mathrm{d} H_t(w) < \log \Big(\int_{{{\Delta}}^1} w\,\mathrm{d} H_t(w)\Big)=0. \end{align*}
\begin{align*} & \mathbb{E}({{Z}}_t)=\int_{{{\mathbb{R}}}} z \,\mathrm{d}G_t(z)= \int_{{{\mathbb{R}}}} \int\limits_{0}^z \,\mathrm{d}u\, \,\mathrm{d}G_t(z) =-\int\limits_{-\infty}^0 G_t(z)\,\mathrm{d}{z} + \int\limits_{0}^{\infty} [1 - G_t(z)]\,\mathrm{d}{z}\\& =-\int\limits_{0}^{1/2} \int\limits_0^u (1-w)\,\mathrm{d} H_t(w)\,\mathrm{d}\log\Big(\frac{u}{1-u}\Big) + \int\limits_{1/2}^{1} \int\limits_u^1 (1-w)\,\mathrm{d} H_t(w)\,\mathrm{d}\log\Big(\frac{u}{1-u}\Big) \\ & =-\int\limits_{0}^{1/2} \int\limits_w^{1/2} \bigg[\mathrm{d}\log\Big(\frac{u}{1-u}\Big)\bigg]\, (1-w)\,\mathrm{d} H_t(w) + \int\limits_{1/2}^{1} \int\limits_{1/2}^w \bigg[\mathrm{d}\log\Big(\frac{u}{1-u}\Big)\bigg]\,(1-w)\,\mathrm{d} H_t(w) \\ & = \int_{{{\Delta}}^1} \log\{w/(1-w)\}\, (1-w)\,\mathrm{d} H_t(w) < \log \Big(\int_{{{\Delta}}^1} w\,\mathrm{d} H_t(w)\Big)=0. \end{align*}
The strict inequality follows from Jensen’s inequality, the strict concavity of the
![]() $\log$
function, and Assumption 2 (ii), which requires
$\log$
function, and Assumption 2 (ii), which requires
![]() $G_t$
to be a non-degenerate distribution. The latter ensures that
$G_t$
to be a non-degenerate distribution. The latter ensures that
![]() $H_t\neq 2\,\delta_{1/2}$
, where
$H_t\neq 2\,\delta_{1/2}$
, where
![]() $\delta_{x}$
denotes the Dirac measure at
$\delta_{x}$
denotes the Dirac measure at
![]() $\{x\}$
.
$\{x\}$
.
Proof of Corollary 2. First we prove the statement that
![]() $\alpha_i<1$
for all
$\alpha_i<1$
for all
![]() $i\ge k$
if the recurrence relation (20) holds. Let
$i\ge k$
if the recurrence relation (20) holds. Let
![]() $\alpha^\star_{t-k\,:\,t-1}\,:\!=\,\max \boldsymbol{\alpha}_{t-k\,:\,t-1}$
; then when
$\alpha^\star_{t-k\,:\,t-1}\,:\!=\,\max \boldsymbol{\alpha}_{t-k\,:\,t-1}$
; then when
![]() $t=k$
we have
$t=k$
we have
![]() $\alpha^\star_{0\,:\,k-1}=1$
by the conditions of Corollary 2, as
$\alpha^\star_{0\,:\,k-1}=1$
by the conditions of Corollary 2, as
![]() $\alpha_0=1$
. From the relation (20) with
$\alpha_0=1$
. From the relation (20) with
![]() $t=k$
we have that
$t=k$
we have that
![]() $\alpha_k=a(\boldsymbol{\alpha}_{0:k-1})\le a\big(\alpha^\star_{0\,:\,k-1} {\textbf{1}}_k \big)= \alpha^\star_{0:k-1} a({\textbf{1}}_k)<1\times 1=1$
. Here, the first inequality comes from the order-preserving property of a, and the second-to-last equality comes from a being 1-homogeneous. The result
$\alpha_k=a(\boldsymbol{\alpha}_{0:k-1})\le a\big(\alpha^\star_{0\,:\,k-1} {\textbf{1}}_k \big)= \alpha^\star_{0:k-1} a({\textbf{1}}_k)<1\times 1=1$
. Here, the first inequality comes from the order-preserving property of a, and the second-to-last equality comes from a being 1-homogeneous. The result
![]() $\alpha_t<1$
for all
$\alpha_t<1$
for all
![]() $t\ge k$
follows from induction over
$t\ge k$
follows from induction over
![]() $t\ge k$
, noting that all
$t\ge k$
, noting that all
![]() $\alpha^\star_{t-k:t-1}<1$
for
$\alpha^\star_{t-k:t-1}<1$
for
![]() $t\ge k+1$
.
$t\ge k+1$
.
For the remainder of the proof it suffices to show that for
![]() $a_t(x)=\alpha_t \,x$
and
$a_t(x)=\alpha_t \,x$
and
![]() $b_t(x)=x^\beta$
, with
$b_t(x)=x^\beta$
, with
![]() $\alpha_t$
given by (20), the convergence (8) holds true with
$\alpha_t$
given by (20), the convergence (8) holds true with
![]() $\psi_t^a({\boldsymbol{z}})=\nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}$
and
$\psi_t^a({\boldsymbol{z}})=\nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}$
and
![]() $\psi_t^b({\boldsymbol{z}})=b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
, and that
$\psi_t^b({\boldsymbol{z}})=b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
, and that
![]() $\alpha_t\to 0$
as
$\alpha_t\to 0$
as
![]() $t\to\infty$
. Since a is twice continuously differentiable, we have
$t\to\infty$
. Since a is twice continuously differentiable, we have
 \begin{eqnarray*} & & v^{-\beta}[a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v + v^\beta\,{\boldsymbol{z}}_v)- a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v)] = \\ & & = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v)\cdot {\boldsymbol{z}}_v + v^{\beta} {\boldsymbol{z}}_v^\top \nabla \nabla^\top a(\boldsymbol{\alpha}_{t-k\,:\,t-1}v) {\boldsymbol{z}}_v + O\big(v^{2(\beta-1)}\big)\\ && = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}_v + v^{\beta-1} {\boldsymbol{z}}_v^\top \nabla \nabla^\top a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) {\boldsymbol{z}}_v + o\big(v^{\beta-1}\big)\quad \text{as $v\to\infty$}, \end{eqnarray*}
\begin{eqnarray*} & & v^{-\beta}[a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v + v^\beta\,{\boldsymbol{z}}_v)- a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v)] = \\ & & = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v)\cdot {\boldsymbol{z}}_v + v^{\beta} {\boldsymbol{z}}_v^\top \nabla \nabla^\top a(\boldsymbol{\alpha}_{t-k\,:\,t-1}v) {\boldsymbol{z}}_v + O\big(v^{2(\beta-1)}\big)\\ && = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}_v + v^{\beta-1} {\boldsymbol{z}}_v^\top \nabla \nabla^\top a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) {\boldsymbol{z}}_v + o\big(v^{\beta-1}\big)\quad \text{as $v\to\infty$}, \end{eqnarray*}
where the last equality follows because a is 1-homogeneous, which gives that
Similarly, because b is continuous and
![]() $\beta$
-homogeneous with
$\beta$
-homogeneous with
![]() $\beta\in[0,1)$
, this gives
$\beta\in[0,1)$
, this gives
![]() $v^{-\beta}b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v + v^\beta\,{\boldsymbol{z}}_v\big) = b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} + v^{\beta-1}\,{\boldsymbol{z}}_v\big) \to b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
, as
$v^{-\beta}b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1}\,v + v^\beta\,{\boldsymbol{z}}_v\big) = b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} + v^{\beta-1}\,{\boldsymbol{z}}_v\big) \to b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
, as
![]() $v\to\infty$
. Hence the convergence (8) holds true with
$v\to\infty$
. Hence the convergence (8) holds true with
![]() $\psi_t^a({\boldsymbol{z}})=\nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}$
and
$\psi_t^a({\boldsymbol{z}})=\nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1})\cdot {\boldsymbol{z}}$
and
![]() $\psi_t^b({\boldsymbol{z}})=b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
.
$\psi_t^b({\boldsymbol{z}})=b(\boldsymbol{\alpha}_{t-k\,:\,t-1})$
.
Lastly, we show that
![]() $\alpha_t\to 0$
as
$\alpha_t\to 0$
as
![]() $t\to \infty$
. Let
$t\to \infty$
. Let
![]() $f: {{{\mathbb{R}}}}_+^k\rightarrow {{{\mathbb{R}}}}_+^k$
with
$f: {{{\mathbb{R}}}}_+^k\rightarrow {{{\mathbb{R}}}}_+^k$
with
![]() $f({\boldsymbol{x}}_{0\,:\,k-1})=({\boldsymbol{x}}_{1\,:\,k-1},a({\boldsymbol{x}}_{0\,:\,k-1}))$
for all
$f({\boldsymbol{x}}_{0\,:\,k-1})=({\boldsymbol{x}}_{1\,:\,k-1},a({\boldsymbol{x}}_{0\,:\,k-1}))$
for all
![]() ${\boldsymbol{x}}_{0\,:\,k-1}\in {{{\mathbb{R}}}}_+^k$
. Let
${\boldsymbol{x}}_{0\,:\,k-1}\in {{{\mathbb{R}}}}_+^k$
. Let
![]() $r^t = f^{k t} \,:\!=\, f\circ f \circ \cdots \circ f$
,
$r^t = f^{k t} \,:\!=\, f\circ f \circ \cdots \circ f$
,
![]() $f^0\,:\!=\,\text{id}$
,
$f^0\,:\!=\,\text{id}$
,
![]() $t=0,1,\ldots$
, denote the (k t)-fold composition of f with itself. Since a is assumed order-preserving and 1-homogeneous, with
$t=0,1,\ldots$
, denote the (k t)-fold composition of f with itself. Since a is assumed order-preserving and 1-homogeneous, with
![]() $a({\textbf{1}}_k) < 1$
, it follows that the function r is also an order-preserving 1-homogeneous function, mapping
$a({\textbf{1}}_k) < 1$
, it follows that the function r is also an order-preserving 1-homogeneous function, mapping
![]() ${{{\mathbb{R}}}}_+^k$
into
${{{\mathbb{R}}}}_+^k$
into
![]() ${{{\mathbb{R}}}}_+^k$
, with
${{{\mathbb{R}}}}_+^k$
, with
![]() $r({\textbf{1}}_k) < {\textbf{1}}_k$
componentwise. Since
$r({\textbf{1}}_k) < {\textbf{1}}_k$
componentwise. Since
![]() $\boldsymbol{\alpha}_{0\,:\,k-1}\in [0,1]^k$
and r is order-preserving, we have
$\boldsymbol{\alpha}_{0\,:\,k-1}\in [0,1]^k$
and r is order-preserving, we have
![]() $r(\boldsymbol{\alpha}_{0\,:\, k-1})< {\textbf{1}}_k$
componentwise too. The latter inequality implies that there exists
$r(\boldsymbol{\alpha}_{0\,:\, k-1})< {\textbf{1}}_k$
componentwise too. The latter inequality implies that there exists
![]() $\nu \in (0,1)$
such that
$\nu \in (0,1)$
such that
![]() $r(\boldsymbol{\alpha}_{0\,:\, k-1}) \leq \nu {\textbf{1}}_k$
. Similarly, the 2-fold composition of r gives
$r(\boldsymbol{\alpha}_{0\,:\, k-1}) \leq \nu {\textbf{1}}_k$
. Similarly, the 2-fold composition of r gives
![]() $r^2(\boldsymbol{\alpha}_{0\,:\, k-1})=r(r(\boldsymbol{\alpha}_{0\,:\, k-1})) \leq r(\nu {\textbf{1}}_k)=\nu^2 {\textbf{1}}_k$
, where the latter equality follows from the homogeneity of the map r. Likewise, iterating forward yields
$r^2(\boldsymbol{\alpha}_{0\,:\, k-1})=r(r(\boldsymbol{\alpha}_{0\,:\, k-1})) \leq r(\nu {\textbf{1}}_k)=\nu^2 {\textbf{1}}_k$
, where the latter equality follows from the homogeneity of the map r. Likewise, iterating forward yields
![]() $r^t(\boldsymbol{\alpha}_{0\,:\, k-1}) \leq \nu^t {\textbf{1}}_k \to {\textbf{0}}_k$
as
$r^t(\boldsymbol{\alpha}_{0\,:\, k-1}) \leq \nu^t {\textbf{1}}_k \to {\textbf{0}}_k$
as
![]() $t\to \infty$
. The claim is proved upon noting that the function r satisfies
$t\to \infty$
. The claim is proved upon noting that the function r satisfies
![]() $\{r^t(\boldsymbol{\alpha}_{0\,:\, k-1})\,:\,t=0,1,\ldots\} = \{\alpha_t\,:\,t=0,1\ldots\}$
.
$\{r^t(\boldsymbol{\alpha}_{0\,:\, k-1})\,:\,t=0,1,\ldots\} = \{\alpha_t\,:\,t=0,1\ldots\}$
.
Proof of Corollary 3. Let
![]() $\log \beta_t = \log \beta + \log(\max_{i=1,\ldots,k}\beta_{t-i})$
, and consider the convergence (12). For
$\log \beta_t = \log \beta + \log(\max_{i=1,\ldots,k}\beta_{t-i})$
, and consider the convergence (12). For
![]() $t=k$
we have
$t=k$
we have
For
![]() $t=k+1$
we have
$t=k+1$
we have
and for
![]() $t=k + j$
with
$t=k + j$
with
![]() $j\in\{2,\ldots,k-1\}$
we have
$j\in\{2,\ldots,k-1\}$
we have
 \begin{align*} & {{v}}^{-\beta^2}b\big({{v}}^\beta {{z}}_0, \ldots {{v}}^{\beta} {{z}}_{k-j}, {{v}}^{\beta^2} {{z}}_{k-j+1}\ldots, {{v}}^{\beta^2} {{z}}_{k-1} \big) \\& = b\big({{z}}_0, \ldots {{z}}_{k-j}, {{v}}^{\beta(\beta-1)} {{z}}_{k-j+1},\ldots, {{v}}^{\beta(\beta-1)} {{z}}_{k-1} \big) \to b({{z}}_0,\ldots, {{z}}_{k - j}, {\textbf{0}}_{j-1}) \quad \text{as ${{v}}\to\infty$}. \end{align*}
\begin{align*} & {{v}}^{-\beta^2}b\big({{v}}^\beta {{z}}_0, \ldots {{v}}^{\beta} {{z}}_{k-j}, {{v}}^{\beta^2} {{z}}_{k-j+1}\ldots, {{v}}^{\beta^2} {{z}}_{k-1} \big) \\& = b\big({{z}}_0, \ldots {{z}}_{k-j}, {{v}}^{\beta(\beta-1)} {{z}}_{k-j+1},\ldots, {{v}}^{\beta(\beta-1)} {{z}}_{k-1} \big) \to b({{z}}_0,\ldots, {{z}}_{k - j}, {\textbf{0}}_{j-1}) \quad \text{as ${{v}}\to\infty$}. \end{align*}
Iterating forward for
![]() $t=2k,2k+1,\ldots$
, we see that the convergence (12) holds with
$t=2k,2k+1,\ldots$
, we see that the convergence (12) holds with
 \begin{eqnarray*} \psi_t^b({\boldsymbol{z}})&=& \begin{cases} b({{z}}_{0}, {\textbf{0}}_{k-1}) & \text{when $\text{mod}_k(t)=0$},\\ b({{z}}_{0},\ldots, {{z}}_{k-1}) & \text{when $\text{mod}_k(t) = 1$},\\ b({{z}}_{0},\ldots, {{z}}_{k - j}, {\textbf{0}}_{j-1}) & \text{when $\text{mod}_k(t) = j \in \{2,\ldots,k-1\}$}, \end{cases} \end{eqnarray*}
\begin{eqnarray*} \psi_t^b({\boldsymbol{z}})&=& \begin{cases} b({{z}}_{0}, {\textbf{0}}_{k-1}) & \text{when $\text{mod}_k(t)=0$},\\ b({{z}}_{0},\ldots, {{z}}_{k-1}) & \text{when $\text{mod}_k(t) = 1$},\\ b({{z}}_{0},\ldots, {{z}}_{k - j}, {\textbf{0}}_{j-1}) & \text{when $\text{mod}_k(t) = j \in \{2,\ldots,k-1\}$}, \end{cases} \end{eqnarray*}
which completes the proof.
A.5. Convergence of multivariate normal full conditional distribution
Let
![]() ${\boldsymbol{X}}_N = (X_{N,0}, \ldots, X_{N,k}) \sim\mathcal{N}({\textbf{0}}_{k+1}, \boldsymbol{\Sigma})$
, where
${\boldsymbol{X}}_N = (X_{N,0}, \ldots, X_{N,k}) \sim\mathcal{N}({\textbf{0}}_{k+1}, \boldsymbol{\Sigma})$
, where
![]() $\boldsymbol{\Sigma}\in{{{\mathbb{R}}}}^{(k+1)\times (k+1)}$
is a positive definite correlation matrix with
$\boldsymbol{\Sigma}\in{{{\mathbb{R}}}}^{(k+1)\times (k+1)}$
is a positive definite correlation matrix with
![]() $(i+1,j+1)$
element
$(i+1,j+1)$
element
![]() $\rho_{ij}$
,
$\rho_{ij}$
,
![]() $i,j=0,\ldots,k$
. Let
$i,j=0,\ldots,k$
. Let
![]() ${\boldsymbol{Q}}= \boldsymbol{\Sigma}^{-1}$
and write
${\boldsymbol{Q}}= \boldsymbol{\Sigma}^{-1}$
and write
![]() $q_{ij}$
for its
$q_{ij}$
for its
![]() $(i+1,j+1)$
element,
$(i+1,j+1)$
element,
![]() $i,j=0,\ldots,k$
. For
$i,j=0,\ldots,k$
. For
![]() $k\geq 1$
and
$k\geq 1$
and
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in{{{\mathbb{R}}}}^{k}$
, the conditional distribution of
${\boldsymbol{z}}_{0\,:\,k-1} \in{{{\mathbb{R}}}}^{k}$
, the conditional distribution of
![]() $X_{N,k}$
given
$X_{N,k}$
given
![]() ${\boldsymbol{X}}_{N,0\,:\,k-1} = {\boldsymbol{z}}_{0\,:\,k-1}$
is normal with mean
${\boldsymbol{X}}_{N,0\,:\,k-1} = {\boldsymbol{z}}_{0\,:\,k-1}$
is normal with mean
![]() $-q_{kk}^{-1}\sum_{i=0}^{k-1} q_{ik} \,{{z}}_i$
and variance
$-q_{kk}^{-1}\sum_{i=0}^{k-1} q_{ik} \,{{z}}_i$
and variance
![]() $q_{kk}^{-1}$
. Let
$q_{kk}^{-1}$
. Let
![]() ${\boldsymbol{X}}=(X_0,\ldots, X_k)$
with
${\boldsymbol{X}}=(X_0,\ldots, X_k)$
with
![]() $X_i=-\log\{1-\Phi(X_{N,i})\}$
, so that
$X_i=-\log\{1-\Phi(X_{N,i})\}$
, so that
![]() $X_i\sim \text{Exp}(1)$
for
$X_i\sim \text{Exp}(1)$
for
![]() $i=0,\ldots,k$
. Following the strategy outlined in Section 5.1, we have that for any
$i=0,\ldots,k$
. Following the strategy outlined in Section 5.1, we have that for any
![]() $t\geq k\geq 1$
,
$t\geq k\geq 1$
,
 \begin{eqnarray} {{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) \mid {\boldsymbol{X}}_{0\,:\,k-1}= {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}))\nonumber\\ = \Phi\bigg[q_{kk}^{1/2}\bigg\{\Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\bigg\}\bigg], \end{eqnarray}
\begin{eqnarray} {{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) \mid {\boldsymbol{X}}_{0\,:\,k-1}= {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}))\nonumber\\ = \Phi\bigg[q_{kk}^{1/2}\bigg\{\Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\bigg\}\bigg], \end{eqnarray}
where
and
Now, let
![]() $t=k$
. First, we seek a function a such that the conditional probability in Equation (58) converges to a number
$t=k$
. First, we seek a function a such that the conditional probability in Equation (58) converges to a number
![]() $p\in(0,1)$
. Suppose that this function satisfies
$p\in(0,1)$
. Suppose that this function satisfies
![]() $a({\boldsymbol{a}}_t-k\,:\,t-1(v))\to \infty$
as
$a({\boldsymbol{a}}_t-k\,:\,t-1(v))\to \infty$
as
![]() $v\to \infty$
. Using standard asymptotic series for the cumulative distribution function of the standard normal distribution, we have
$v\to \infty$
. Using standard asymptotic series for the cumulative distribution function of the standard normal distribution, we have
 \begin{eqnarray*} \Phi_{i,{{v}}}^{-1} &=& \{2\,A_{i}({{v}}, {{z}}_i)\}^{1/2} - \frac{\log A_{i}({{v}}, {{z}}_i) + \log 4\pi}{2\{2\,A_{i}({{v}},{{z}}_i)\}^{1/2}}+o(A_{i}({{v}},{{z}}_i)^{-1/2}),\quad i=t-k,\ldots, t-1,\\[3pt] \Phi_{t,{{v}}}^{-1} &=& \{2\,a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))\}^{1/2} - \frac{\log a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})) + \log 4\pi}{2\{2\,a({\boldsymbol{A}}_{t}({\boldsymbol{z}}_{0\,:\,k-1}))\}^{1/2}}\\ && +o(a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))^{-1/2}),\end{eqnarray*}
\begin{eqnarray*} \Phi_{i,{{v}}}^{-1} &=& \{2\,A_{i}({{v}}, {{z}}_i)\}^{1/2} - \frac{\log A_{i}({{v}}, {{z}}_i) + \log 4\pi}{2\{2\,A_{i}({{v}},{{z}}_i)\}^{1/2}}+o(A_{i}({{v}},{{z}}_i)^{-1/2}),\quad i=t-k,\ldots, t-1,\\[3pt] \Phi_{t,{{v}}}^{-1} &=& \{2\,a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))\}^{1/2} - \frac{\log a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})) + \log 4\pi}{2\{2\,a({\boldsymbol{A}}_{t}({\boldsymbol{z}}_{0\,:\,k-1}))\}^{1/2}}\\ && +o(a({\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))^{-1/2}),\end{eqnarray*}
as
![]() $v\to \infty$
. Therefore,
$v\to \infty$
. Therefore,
 \begin{align} & \Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\nonumber\\& = (2 [a\{{\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})\}])^{1/2} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg) \{2\,A_{t-k+i,{{v}}}( {{z}}_i)\}^{1/2} + o(1), \end{align}
\begin{align} & \Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\nonumber\\& = (2 [a\{{\boldsymbol{A}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})\}])^{1/2} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg) \{2\,A_{t-k+i,{{v}}}( {{z}}_i)\}^{1/2} + o(1), \end{align}
as
![]() ${{v}}\to\infty$
. Substituting in (58), we observe that for the choice of a being
${{v}}\to\infty$
. Substituting in (58), we observe that for the choice of a being
![]() $a({\boldsymbol{y}}_{0\,:\,k-1}) = \big\{\sum_{i=0}^{k-1}({-}q_{ik}/q_{kk})\,|y_i|^{1/2}\big\}^2$
, for
$a({\boldsymbol{y}}_{0\,:\,k-1}) = \big\{\sum_{i=0}^{k-1}({-}q_{ik}/q_{kk})\,|y_i|^{1/2}\big\}^2$
, for
![]() ${\boldsymbol{y}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^k$
, the conditions set out in Section 5.1 are met. In particular, since (59) converges to zero and
${\boldsymbol{y}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^k$
, the conditions set out in Section 5.1 are met. In particular, since (59) converges to zero and
![]() $\Phi$
is continuous, we have the conditional probability (58) converging to
$\Phi$
is continuous, we have the conditional probability (58) converging to
![]() $p=1/2$
; that is,
$p=1/2$
; that is,
 \begin{align*} \lim_{{{v}}\to \infty}\Phi\bigg[q_{kk}^{1/2}\bigg\{\Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\bigg\}\bigg] = 1/2.\end{align*}
\begin{align*} \lim_{{{v}}\to \infty}\Phi\bigg[q_{kk}^{1/2}\bigg\{\Phi_{t,{{v}}}^{-1} - \sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\Phi_{t-k+i,{{v}}}^{-1}\bigg\}\bigg] = 1/2.\end{align*}
Using similar asymptotic series, we have that for
![]() $b({\boldsymbol{y}}_{0\,:\,k-1}) = a({\boldsymbol{y}}_{0\,:\,k-1})^{1/2}$
and any
$b({\boldsymbol{y}}_{0\,:\,k-1}) = a({\boldsymbol{y}}_{0\,:\,k-1})^{1/2}$
and any
![]() $x_k \in {{{\mathbb{R}}}}$
,
$x_k \in {{{\mathbb{R}}}}$
,
 \begin{align} & \lim_{{{v}} \to \infty}{{\mathbb{P}}}\,(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})+b({\boldsymbol{X}}_{0\,:\,k-1})\,x_{k}\,\Big |\, {\boldsymbol{X}}_{0\,:\,k-1}= {\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))\nonumber\\ & =\Phi\{(q_{kk}/2)^{1/2}\,x_k \}. \end{align}
\begin{align} & \lim_{{{v}} \to \infty}{{\mathbb{P}}}\,(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})+b({\boldsymbol{X}}_{0\,:\,k-1})\,x_{k}\,\Big |\, {\boldsymbol{X}}_{0\,:\,k-1}= {\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))\nonumber\\ & =\Phi\{(q_{kk}/2)^{1/2}\,x_k \}. \end{align}
The convergence in (60) holds uniformly on compact sets in the variable
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (60) holds true if we replace
${\boldsymbol{z}}_{0\,:\,k-1}$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (60) holds true if we replace
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
by
${\boldsymbol{z}}_{0\,:\,k-1}$
by
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}$
as
${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}$
as
![]() ${{v}}\to \infty$
, and since the limit function is continuous in
${{v}}\to \infty$
, and since the limit function is continuous in
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
(constant function), the argument follows. Additionally, we have that for any
${\boldsymbol{z}}_{0\,:\,k-1}$
(constant function), the argument follows. Additionally, we have that for any
![]() $\boldsymbol{\alpha}_{t-k\,:\,t-1}\in(0,1]^k$
,
$\boldsymbol{\alpha}_{t-k\,:\,t-1}\in(0,1]^k$
,
 \begin{eqnarray*} &&\lim_{{{v}}\to\infty}{{v}}^{-1/2}\,\big[a\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}}+{{v}}^{1/2}{\boldsymbol{z}}_{0\,:\,k-1}\big)-a(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}})\big] = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) \cdot {\boldsymbol{z}}_{0\,:\,k-1},\\ &&\lim_{{{v}}\to\infty}{{v}}^{-1/2}\,b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}}+{{v}}^{1/2}{\boldsymbol{z}}_{0\,:\,k-1}\big)=b(\boldsymbol{\alpha}_{t-k\,:\,t-1}),\end{eqnarray*}
\begin{eqnarray*} &&\lim_{{{v}}\to\infty}{{v}}^{-1/2}\,\big[a\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}}+{{v}}^{1/2}{\boldsymbol{z}}_{0\,:\,k-1}\big)-a(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}})\big] = \nabla a(\boldsymbol{\alpha}_{t-k\,:\,t-1}) \cdot {\boldsymbol{z}}_{0\,:\,k-1},\\ &&\lim_{{{v}}\to\infty}{{v}}^{-1/2}\,b\big(\boldsymbol{\alpha}_{t-k\,:\,t-1} \, {{v}}+{{v}}^{1/2}{\boldsymbol{z}}_{0\,:\,k-1}\big)=b(\boldsymbol{\alpha}_{t-k\,:\,t-1}),\end{eqnarray*}
where both convergences hold uniformly on compact sets in the variable
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
, since monotone increasing functions (in every argument) converge pointwise to a continuous limit. Thus, Assumption 3 holds true for the special case
${\boldsymbol{z}}_{0\,:\,k-1}$
, since monotone increasing functions (in every argument) converge pointwise to a continuous limit. Thus, Assumption 3 holds true for the special case
![]() $t=k$
with
$t=k$
with
 \begin{align*}a_t({{v}})=\Bigg\{\sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\rho_{t-k+i}^{1/2}\Bigg\}^2\,{{v}}\quad \text{and}\quad b_t({{v}})={{v}}^{1/2}. \end{align*}
\begin{align*}a_t({{v}})=\Bigg\{\sum_{i=0}^{k-1}\bigg({-}\frac{q_{ik}}{q_{kk}}\bigg)\,\rho_{t-k+i}^{1/2}\Bigg\}^2\,{{v}}\quad \text{and}\quad b_t({{v}})={{v}}^{1/2}. \end{align*}
Finally, observe that the entire argument after (58) remains unchanged if we change
![]() $t=k$
to
$t=k$
to
![]() $t = k+1$
. The claim is proved through iteration.
$t = k+1$
. The claim is proved through iteration.
A.6. Convergence of multivariate inverted logistic full conditional distribution
The transition probability kernel of this process is given by (35) with
![]() $V({\boldsymbol{x}})=\lVert {\boldsymbol{x}}^{-1/\alpha}\rVert^{\alpha}$
,
$V({\boldsymbol{x}})=\lVert {\boldsymbol{x}}^{-1/\alpha}\rVert^{\alpha}$
,
![]() ${\boldsymbol{x}} \in {{{\mathbb{R}}}}_+^{k+1}$
. For
${\boldsymbol{x}} \in {{{\mathbb{R}}}}_+^{k+1}$
. For
![]() $t\geq k\geq 1$
and
$t\geq k\geq 1$
and
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}_+^{k}$
, we have that
${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}_+^{k}$
, we have that
![]() ${{\mathbb{P}}}(X_k/b({\boldsymbol{X}}_{0\,:\,k-1})<1\mid {\boldsymbol{X}}_{0\,:\,k-1}={\boldsymbol{B}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}) )$
is equal to
${{\mathbb{P}}}(X_k/b({\boldsymbol{X}}_{0\,:\,k-1})<1\mid {\boldsymbol{X}}_{0\,:\,k-1}={\boldsymbol{B}}_{t}({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}) )$
is equal to
where
![]() ${\boldsymbol{B}}_{t}({{v}},{\boldsymbol{z}}_{0\,:\,k-1}) = (B_{t-k}({{v}}, {{z}}_{0}),\ldots,B_{t-1}({{v}},{{z}}_{k-1})) $
and
${\boldsymbol{B}}_{t}({{v}},{\boldsymbol{z}}_{0\,:\,k-1}) = (B_{t-k}({{v}}, {{z}}_{0}),\ldots,B_{t-1}({{v}},{{z}}_{k-1})) $
and
![]() $\mathscr{L}(v, {\boldsymbol{z}}_{0\,:\,k-1})=1+o(1)$
for all
$\mathscr{L}(v, {\boldsymbol{z}}_{0\,:\,k-1})=1+o(1)$
for all
![]() ${\boldsymbol{z}}_{0\,:\,k-1}\in {{{\mathbb{R}}}}_+^k$
as
${\boldsymbol{z}}_{0\,:\,k-1}\in {{{\mathbb{R}}}}_+^k$
as
![]() $v\to\infty$
.
$v\to\infty$
.
Now let
![]() $t=k$
and set
$t=k$
and set
![]() $z_0 = 1$
. First, we seek a function b such that the conditional probability in Equation (61) converges to a number
$z_0 = 1$
. First, we seek a function b such that the conditional probability in Equation (61) converges to a number
![]() $p\in(0,1)$
. Suppose that this function satisfies
$p\in(0,1)$
. Suppose that this function satisfies
![]() $b({\boldsymbol{b}}_{0\,:\,k-1}({{v}}))\to \infty$
as
$b({\boldsymbol{b}}_{0\,:\,k-1}({{v}}))\to \infty$
as
![]() ${{v}}\to \infty$
with
${{v}}\to \infty$
with
![]() $b({\boldsymbol{b}}_{0\,:\,k-1}({{v}})) = o({{v}})$
. Under this assumption, we have that as
$b({\boldsymbol{b}}_{0\,:\,k-1}({{v}})) = o({{v}})$
. Under this assumption, we have that as
![]() ${{v}} \to \infty$
,
${{v}} \to \infty$
,

This expression converges to a positive constant provided
 \begin{align*} b({\boldsymbol{B}}({{v}},{\boldsymbol{z}}_{0\,:\,k-1})) = \mathcal{O}\Bigg[\Bigg\{ \sum_{i=0}^{k-1} B_{t}({{v}},{{z}}_{i})^{1/\alpha}\Bigg\}^{\alpha(1-\alpha)}\Bigg]\quad \text{as ${{v}} \to \infty$}.\end{align*}
\begin{align*} b({\boldsymbol{B}}({{v}},{\boldsymbol{z}}_{0\,:\,k-1})) = \mathcal{O}\Bigg[\Bigg\{ \sum_{i=0}^{k-1} B_{t}({{v}},{{z}}_{i})^{1/\alpha}\Bigg\}^{\alpha(1-\alpha)}\Bigg]\quad \text{as ${{v}} \to \infty$}.\end{align*}
Hence, choosing b equal to
![]() $b({\boldsymbol{y}}) = \lVert {\boldsymbol{y}}^{1/\alpha}\lVert^{\alpha (1-\alpha)}$
,
$b({\boldsymbol{y}}) = \lVert {\boldsymbol{y}}^{1/\alpha}\lVert^{\alpha (1-\alpha)}$
,
![]() ${\boldsymbol{y}} \in {{{\mathbb{R}}}}_+^{k}$
, gives the conditional probability (61) converging to
${\boldsymbol{y}} \in {{{\mathbb{R}}}}_+^{k}$
, gives the conditional probability (61) converging to
![]() $p=1-\exp({-}\alpha)$
, that is,
$p=1-\exp({-}\alpha)$
, that is,
and generally, we also have that for any
![]() $x_k\in {{{\mathbb{R}}}}_+$
,
$x_k\in {{{\mathbb{R}}}}_+$
,
Lastly, we note that the convergence in (62) holds uniformly on compact sets in the variable
![]() ${\boldsymbol{x}}_{0\,:\,k-1}\in [\delta_1,\infty)\times\cdots\times [\delta_k,\infty)$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (62) holds true if we replace
${\boldsymbol{x}}_{0\,:\,k-1}\in [\delta_1,\infty)\times\cdots\times [\delta_k,\infty)$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (62) holds true if we replace
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
by
${\boldsymbol{z}}_{0\,:\,k-1}$
by
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}\in[\delta_1,\infty)\times \cdots\times [\delta_k, \infty)$
as
${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}\in[\delta_1,\infty)\times \cdots\times [\delta_k, \infty)$
as
![]() ${{v}}\to \infty$
, and since the limit function is continuous in
${{v}}\to \infty$
, and since the limit function is continuous in
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
(constant function), the argument follows.
${\boldsymbol{z}}_{0\,:\,k-1}$
(constant function), the argument follows.
Let
![]() $\beta_t$
satisfy the recurrence relation
$\beta_t$
satisfy the recurrence relation
![]() $\log \beta_t = \log (1-\alpha) +\log(\max_{i=1,\ldots,k}\beta_{t-i})$
subject to
$\log \beta_t = \log (1-\alpha) +\log(\max_{i=1,\ldots,k}\beta_{t-i})$
subject to
![]() $\beta_{i} = 1-\alpha$
for
$\beta_{i} = 1-\alpha$
for
![]() $i=1,\ldots,k-1$
. For all
$i=1,\ldots,k-1$
. For all
![]() $\delta_1,\ldots,\delta_k > 0$
and
$\delta_1,\ldots,\delta_k > 0$
and
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in [\delta_1,\infty) \times\ldots \times$
${\boldsymbol{z}}_{0\,:\,k-1} \in [\delta_1,\infty) \times\ldots \times$
![]() $[\delta_k,\infty)$
,
$[\delta_k,\infty)$
,
where
![]() $\psi_t^b>0$
is continuous and has the same form as in Corollary 3. Thus, Assumption 5 holds for the special case
$\psi_t^b>0$
is continuous and has the same form as in Corollary 3. Thus, Assumption 5 holds for the special case
![]() $t=k$
with
$t=k$
with
![]() $b_t({{v}})={{v}}^{\beta_t}$
.
$b_t({{v}})={{v}}^{\beta_t}$
.
Finally, observe that the entire argument after (61) remains unchanged if we change
![]() $t=k$
to
$t=k$
to
![]() $t = k+1$
. The claim is proved through iteration.
$t = k+1$
. The claim is proved through iteration.
A.7. Convergence of max-stable full conditional distribution—no mass on boundary
Suppose that
![]() $a({{v}}{\textbf{1}}_k)\to \infty$
as
$a({{v}}{\textbf{1}}_k)\to \infty$
as
![]() ${{v}}\to \infty$
. Let
${{v}}\to \infty$
. Let
![]() $\Pi_{k-1}$
denote the set of partitions of
$\Pi_{k-1}$
denote the set of partitions of
![]() $[k-1]=\{0,\ldots,k-1\}$
. Then, for
$[k-1]=\{0,\ldots,k-1\}$
. Then, for
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
and with some rearrangement,
${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
and with some rearrangement,
![]() ${{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) \mid {\boldsymbol{X}}_{0\,:\,k-1} = {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}) )$
is equal to
${{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) \mid {\boldsymbol{X}}_{0\,:\,k-1} = {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}) )$
is equal to
 \begin{eqnarray} && \frac{1+ \sum_{p \in \Pi_{k-1}{{\setminus}} [k-1] }({-}1)^{\lvert p \lvert} \{\prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k})\}/ V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k})} {1+\sum_{p \in \Pi_{k-1} {{\setminus}} [k-1]}({-}1)^{\lvert p\lvert} \{\prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k-1}, \infty)\}/V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, \infty)}\nonumber\\\nonumber\\ && \times \frac{V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k})} {V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, \infty)}\times \exp\{V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) - V({\boldsymbol{y}}_{0\,:\,k})\}, \end{eqnarray}
\begin{eqnarray} && \frac{1+ \sum_{p \in \Pi_{k-1}{{\setminus}} [k-1] }({-}1)^{\lvert p \lvert} \{\prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k})\}/ V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k})} {1+\sum_{p \in \Pi_{k-1} {{\setminus}} [k-1]}({-}1)^{\lvert p\lvert} \{\prod_{J \in p} V_J({\boldsymbol{y}}_{0\,:\,k-1}, \infty)\}/V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, \infty)}\nonumber\\\nonumber\\ && \times \frac{V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k})} {V_{0\,:\,k-1}({\boldsymbol{y}}_{0\,:\,k-1}, \infty)}\times \exp\{V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) - V({\boldsymbol{y}}_{0\,:\,k})\}, \end{eqnarray}
where
Since
![]() $V_J$
is a
$V_J$
is a
![]() $-(\vert J \vert+1)$
-homogeneous function [Reference Coles and Tawn4], it follows that
$-(\vert J \vert+1)$
-homogeneous function [Reference Coles and Tawn4], it follows that
as
![]() ${{v}}\to \infty$
. Because
${{v}}\to \infty$
. Because
![]() $\lvert p \rvert \geq 2$
for any
$\lvert p \rvert \geq 2$
for any
![]() $p\in \Pi_{k-1} {{\setminus}} [k-1]$
, it follows that the first fraction in (63) converges to unity as
$p\in \Pi_{k-1} {{\setminus}} [k-1]$
, it follows that the first fraction in (63) converges to unity as
![]() ${{v}}\to \infty$
, whereas the homogeneity property of the exponent function V also guarantees that the last term in (63) converges to unity since
${{v}}\to \infty$
, whereas the homogeneity property of the exponent function V also guarantees that the last term in (63) converges to unity since
![]() $V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) = \mathcal{O}\{\exp({-}{{v}})\}$
and
$V({\boldsymbol{y}}_{0\,:\,k-1}, \infty) = \mathcal{O}\{\exp({-}{{v}})\}$
and
![]() $V({\boldsymbol{y}}_{0\,:\,k}) = \mathcal{O}\{\exp({-}{{v}})\}$
. This leads to
$V({\boldsymbol{y}}_{0\,:\,k}) = \mathcal{O}\{\exp({-}{{v}})\}$
. This leads to
as
![]() ${{v}} \to \infty$
. Therefore, for any functional a satisfying the property (19), we have
${{v}} \to \infty$
. Therefore, for any functional a satisfying the property (19), we have
Similarly, for
![]() $x_k \in {{{\mathbb{R}}}}$
,
$x_k \in {{{\mathbb{R}}}}$
,
![]() ${{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) + x_k \mid {\boldsymbol{X}}_{0\,:\,k-1} = {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}))$
converges to K given by (42). The convergence in (66) holds uniformly on compact sets in the variable
${{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1}) + x_k \mid {\boldsymbol{X}}_{0\,:\,k-1} = {\boldsymbol{A}}_t({{v}},{\boldsymbol{z}}_{0\,:\,k-1}))$
converges to K given by (42). The convergence in (66) holds uniformly on compact sets in the variable
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (66) holds true if we replace
${\boldsymbol{z}}_{0\,:\,k-1}$
by continuous convergence (see Section 0.1 in [Reference Resnick25]). That is, (66) holds true if we replace
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
by
${\boldsymbol{z}}_{0\,:\,k-1}$
by
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
${\boldsymbol{z}}_{0\,:\,k-1}({{v}})$
satisfying
![]() ${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}$
as
${\boldsymbol{z}}_{0\,:\,k-1}({{v}}) \to {\boldsymbol{z}}_{0\,:\,k-1}$
as
![]() ${{v}}\to \infty$
, and since the limit function is continuous in
${{v}}\to \infty$
, and since the limit function is continuous in
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
, the argument follows.
${\boldsymbol{z}}_{0\,:\,k-1}$
, the argument follows.
A.8. Convergence of logistic full conditional distribution
Under Assumption 3, (65) implies that for all
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
,
${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
,
 \begin{eqnarray*} {{\mathbb{P}}}\,(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})\mid {\boldsymbol{X}}_{0\,:\,k-1}&=&{\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))= \bigg[1 + \frac{\exp\{-a({\boldsymbol{y}}_{0\,:\,k-1})/\alpha\}}{\big\lVert \exp({-}{\boldsymbol{y}}_{0\,:\,k-1}/\alpha) \big\lVert} \bigg]^{ \alpha-k} \\ && \times (1+o(1))\end{eqnarray*}
\begin{eqnarray*} {{\mathbb{P}}}\,(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})\mid {\boldsymbol{X}}_{0\,:\,k-1}&=&{\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))= \bigg[1 + \frac{\exp\{-a({\boldsymbol{y}}_{0\,:\,k-1})/\alpha\}}{\big\lVert \exp({-}{\boldsymbol{y}}_{0\,:\,k-1}/\alpha) \big\lVert} \bigg]^{ \alpha-k} \\ && \times (1+o(1))\end{eqnarray*}
as
![]() ${{v}}\to\infty$
, where
${{v}}\to\infty$
, where
![]() ${\boldsymbol{y}}_{0\,:\,k-1} = -1/\log[1-\exp\{- {\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})\}]$
. Choosing a to be
${\boldsymbol{y}}_{0\,:\,k-1} = -1/\log[1-\exp\{- {\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1})\}]$
. Choosing a to be
![]() $a({\boldsymbol{z}}_{0\,:\,k-1}) = -\alpha \log\,\{ \lVert \exp({-}{\boldsymbol{z}}_{0\,:\,k-1}/\alpha)\rVert\}$
, we see that
$a({\boldsymbol{z}}_{0\,:\,k-1}) = -\alpha \log\,\{ \lVert \exp({-}{\boldsymbol{z}}_{0\,:\,k-1}/\alpha)\rVert\}$
, we see that
and more generally, for any
![]() $x_k \in {{{\mathbb{R}}}}$
,
$x_k \in {{{\mathbb{R}}}}$
,
The limit distribution does not depend on
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
since a satisfies the property (19).
${\boldsymbol{z}}_{0\,:\,k-1}$
since a satisfies the property (19).
A.9. Convergence of Hüsler–Reiss full conditional distribution
Equation (15) of [Reference Wadsworth and Tawn34] and (65) imply that for all
![]() ${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
,
${\boldsymbol{z}}_{0\,:\,k-1} \in {{{\mathbb{R}}}}^{k}$
,
as
![]() ${{v}}\to\infty$
. Here
${{v}}\to\infty$
. Here
![]() $\Phi$
denotes the cumulative distribution function of the standard normal distribution, and
$\Phi$
denotes the cumulative distribution function of the standard normal distribution, and
![]() $\mu({\boldsymbol{y}}_{0\,:\,k-1}) = - \tau \big({\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\boldsymbol{y}}_{0\,:\,k-1} + {\boldsymbol{K}}_{01}^\top \boldsymbol{\Sigma}^{-1}{\textbf{1}}_{k+1}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)$
, where
$\mu({\boldsymbol{y}}_{0\,:\,k-1}) = - \tau \big({\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\boldsymbol{y}}_{0\,:\,k-1} + {\boldsymbol{K}}_{01}^\top \boldsymbol{\Sigma}^{-1}{\textbf{1}}_{k+1}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)$
, where
![]() $\tau^{-1}={\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{01}$
,
$\tau^{-1}={\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{01}$
,
![]() ${\boldsymbol{C}}=\big(\boldsymbol{\Sigma}^{-1} - {\boldsymbol{q}} {\boldsymbol{q}}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)$
is a
${\boldsymbol{C}}=\big(\boldsymbol{\Sigma}^{-1} - {\boldsymbol{q}} {\boldsymbol{q}}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)$
is a
![]() $(k+1)\times (k+1)$
matrix of rank k,
$(k+1)\times (k+1)$
matrix of rank k,
![]() ${\boldsymbol{q}}=\boldsymbol{\Sigma}^{-1}\,{\textbf{1}}_{k+1}$
, and
${\boldsymbol{q}}=\boldsymbol{\Sigma}^{-1}\,{\textbf{1}}_{k+1}$
, and
Choosing a to be
![]() $a({\boldsymbol{z}}_{0\,:\,k-1}) = -\tau {\boldsymbol{K}}_{01}^\top{\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\boldsymbol{z}}_{0\,:\,k-1}$
, we see that for any
$a({\boldsymbol{z}}_{0\,:\,k-1}) = -\tau {\boldsymbol{K}}_{01}^\top{\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\boldsymbol{z}}_{0\,:\,k-1}$
, we see that for any
![]() $x_k\in{{{\mathbb{R}}}}$
,
$x_k\in{{{\mathbb{R}}}}$
,
 \begin{align*} & \lim_{{{v}}\to \infty}{{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})+x_k \mid {\boldsymbol{X}}_{0\,:\,k-1})\\& ={\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))=\Phi\big[\big\{x_k+\tau \big({\boldsymbol{K}}_{01}^\top \boldsymbol{\Sigma}^{-1}{\textbf{1}}_{k+1}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)\big\}/\tau\big].\end{align*}
\begin{align*} & \lim_{{{v}}\to \infty}{{\mathbb{P}}}(X_k < a({\boldsymbol{X}}_{0\,:\,k-1})+x_k \mid {\boldsymbol{X}}_{0\,:\,k-1})\\& ={\boldsymbol{A}}_t({{v}}, {\boldsymbol{z}}_{0\,:\,k-1}))=\Phi\big[\big\{x_k+\tau \big({\boldsymbol{K}}_{01}^\top \boldsymbol{\Sigma}^{-1}{\textbf{1}}_{k+1}^\top/{\textbf{1}}_{k+1}^\top {\boldsymbol{q}}\big)\big\}/\tau\big].\end{align*}
The limit distribution does not depend on
![]() ${\boldsymbol{z}}_{0\,:\,k-1}$
, since a satisfies the property (19). The latter follows from the properties
${\boldsymbol{z}}_{0\,:\,k-1}$
, since a satisfies the property (19). The latter follows from the properties
![]() ${\boldsymbol{K}}_{10}\cdot {\textbf{1}}_{k} = {\textbf{1}}_{k+1} - {\boldsymbol{K}}_{01}$
and
${\boldsymbol{K}}_{10}\cdot {\textbf{1}}_{k} = {\textbf{1}}_{k+1} - {\boldsymbol{K}}_{01}$
and
![]() ${\boldsymbol{C}} \cdot {\textbf{1}}_{k+1} = {\textbf{0}}_{k+1, 1}$
, which give
${\boldsymbol{C}} \cdot {\textbf{1}}_{k+1} = {\textbf{0}}_{k+1, 1}$
, which give
![]() $-\tau \, {\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\textbf{1}}_{k} = 1$
.
$-\tau \, {\boldsymbol{K}}_{01}^\top {\boldsymbol{C}} {\boldsymbol{K}}_{10} \cdot {\textbf{1}}_{k} = 1$
.
Acknowledgements
I. Papastathopoulos expresses his appreciation to Bas Lemmens for insightful discussions regarding fixed points of topical and homogeneous functions, and to Laurens de Haan for enlightening discussions on properties of extended regularly varying functions. We also thank the referees and editors for very helpful suggestions that have improved the presentation of the paper.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.