Hostname: page-component-5cf477f64f-h6p2m Total loading time: 0 Render date: 2025-04-08T14:02:45.249Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for convex hulls of random sets

Part of: Geometric probability and stochastic geometry Real functions: Miscellaneous topics Stochastic processes

Published online by Cambridge University Press:  01 July 2016

Ilya S. Molchanov
Ilya S. Molchanov*
Affiliation:
Kiev Technological Institute
*
∗Permanent address: Kiev Technological Institute of Food Industry, Vladimirskaya, 68, Kiev, 252017, Ukraine. Currently visiting Bergakademie Freiberg, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 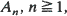, be i.i.d. random closed sets in 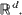. Limit theorems for their normalized convex hulls 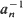conv (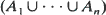) are proved. The limiting distributions correspond to C-stable random sets. The random closed set A is called C-stable if, for any 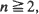, the sets anA and conv ( 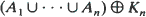coincide in distribution for certain positive an, compact Kn, and independent copies A1, …, An of A. The distributions of C-stable sets are characterized via corresponding containment functionals.

Keywords

CONTAINMENT FUNCTIONALSTABLE DISTRIBUTIONREGULAR VARIATIONRANDOM SETPROBABILITY DISTRIBUTIONMAX-STABILITYRANDOM SAMPLEMULTIVALUED FUNCTION

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 26E25: Set-valued functions 60G70: Extreme value theory; extremal processes
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 2 , June 1993 , pp. 395 - 414
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balkema, A. A. and Resnick, S. I. (1977) Max-infinite divisibility. J. Appl. Prob. 14, 309–319.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Choquet, G. (1953/54) Theory of capacities. Ann. Inst. Fourier 5, 131–295.CrossRefGoogle Scholar
Cressie, N. (1979) A central limit theorem for random sets. Z. Wahrscheinlichkeitsth. 49, 37–47.CrossRefGoogle Scholar
Davis, R. A., Mulrow, E. and Resnick, S. I. (1988) Almost sure limit sets of random samples in ℝ d . Adv. Appl. Prob. 20, 573–599.Google Scholar
Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
Gine, E., Hahn, M. G. and Zinn, J. (1983) Limit theorems for random sets: an application of probability in Banach space results. Lecture Notes in Mathematics 990, 112–135, Springer-Verlag, Berlin.Google Scholar
Gine, E., Hahn, M. G. and Vatan, P. (1990) Max-infinitely divisible and max-stable sample continuous processes. Probab. Theory Relat. Fields 87, 139–165.Google Scholar
Haan, L. De, and Resnick, S. I. (1987) On regular variation of probability densities. Stoch. Proc. Appl. 25, 83–93.CrossRefGoogle Scholar
Lyashenko, N. N. (1983) Weak convergence of step-processes in the space of closed sets. Notices Leningrad Steklov Math. Inst. 130, 122–129 (in Russian).Google Scholar
Matheron, G. (1975) Random Sets and Integral Geometry. Wiley, New York.Google Scholar
Molchanov, I. S. (1984) A generalization of the Choquet theorem for random sets with a given class of realizations. Theory Prob. Math. Statist. 28, 99–106.Google Scholar
Norberg, T. (1984) Convergence and existence of random set distributions. Ann. Prob. 12, 726–732.Google Scholar
Santalo, L. A. (1976) Integral Geometry and Geometric Probability. Addison-Wesley, Reading, MA.Google Scholar
Schneider, R. (1988) Random approximations of convex sets. J. Microsc. 151, 211–227.Google Scholar
Seneta, E. (1976) Regularly Varying Functions. Springer-Verlag, Berlin.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1987) Stochastic Geometry and Its Applications . Akademie-Verlag, Berlin.Google Scholar
Trader, D. A. (1981) Infinitely Divisible Random Sets. Ph.D. Dissertation, Department of Statistics, Carnegie-Mellon University.Google Scholar
Uryson, P. S. (1924) Dependence between the mean breadth and the volume of convex bodies in the n-dimensional space. Mat. Sb. 31, 477–486 (in Russian).Google Scholar
Vitale, R. A. (1983) Some developments in the theory of random sets. Bull. Internat. Statist. Inst. , 50, 863–871.Google Scholar
Vitale, R. A. (1987) Expected convex hulls, order statistics and Banach space probabilities, Acta Appl. Math. 9, 97–102.CrossRefGoogle Scholar
Vitale, R. A. (1988) An alternate formulation of mean value for random geometric figures. J. Microsc. 151, 197–204.Google Scholar
Weil, W. (1982) An application of the central limit theorem for Banach space-valued random variables to the theory of random sets. Z. Wahrscheinlichkeitsth. 60, 203–208.Google Scholar
Yakimiv, A. L. (1981) Multivariate Tauberian theorems and their application to the branching Bellman–Harris processes. Mat. Sb. 115, 463–467 (in Russian).Google Scholar