Article contents
A New Two-Grid Method for Expanded Mixed Finite Element Solution of Nonlinear Reaction Diffusion Equations
Published online by Cambridge University Press: 17 January 2017
Abstract
In the paper, we present an efficient two-grid method for the approximation of two-dimensional nonlinear reaction-diffusion equations using a expanded mixed finite-element method. We transfer the nonlinear reaction diffusion equation into first order nonlinear equations. The solution of the nonlinear system on the fine space is reduced to the solutions of two small (one linear and one non-linear) systems on the coarse space and a linear system on the fine space. Moreover, we obtain the error estimation for the two-grid algorithm. It is showed that coarse space can be extremely coarse and achieve asymptotically optimal approximation as long as the mesh sizes satisfy 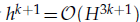 . An numerical example is also given to illustrate the effectiveness of the algorithm.
. An numerical example is also given to illustrate the effectiveness of the algorithm.
- Type
- Research Article
- Information
- Copyright
- Copyright © Global-Science Press 2017
References
- 7
- Cited by


