The values of an era are embedded in objects. They can be difficult for those of different generations to interpret or even recognise; nonetheless, objects offer silent witness to bygone cultural moments. Here I investigate the tacit and explicit meanings of an object in the Whipple Museum’s collection that is at once a mechanical calculator and a depiction of a monkey. This unusual amalgamation offers us a window into the world that made and used it, including how people thought about mathematics, education, and childhood.
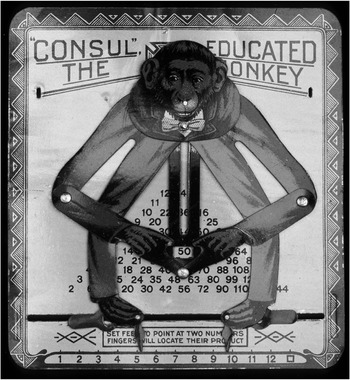
‘“Consul”, the Educated Monkey’ is a 14 cm × 15 cm metal backplate printed with a number chart, to which is attached a moveable monkey figure, wearing a suit and bow tie and made of thin enamelled steel (Figure 11.1).Footnote 2 If you position the monkey’s feet to point at two numbers in a row of 1–12, let’s say 4 and 8, then the monkey’s metal-pin joints force its arms and torso to change position until its hands cradle the two numbers’ product printed on the backplate: 32. The device groans as you gently coax its resistant feet into position, but the rest of Consul’s body moves with the precise coordination of a dancer. Its gritted-teeth smile doesn’t move. The monkey’s pose can be rather gymnastically grotesque for certain calculations. As a fun surprise, as Consul’s head approaches its ankles to multiply far-flung numbers such as 1 and 12, the metal bar connecting its hands and torso sticks up over the monkey’s head, transforming into a strikingly realistic tail painted with brown and black furry stripes. As an additional touch of charm, next to the number 12 is a small empty square, signifying the ‘square’ of the number chosen for the other foot.
The Whipple has displayed this grinning simian beside mechanical calculating devices, such as Napier’s bones and abacuses, and included it in the ‘Science Toys Trail’ activity, illustrating how this object exemplifies several categories of things. This object has always been a hybrid; even its inventor patented it as both a calculator and a plaything. William Henry Robertson filed for two US patents in 1915: the first patent was for ‘certain new and useful Improvements in Calculating Devices’ and the second, filed six months later, was for ‘certain new and useful Improvements in Toys’.Footnote 3 He assigned the rights to the inventions to a company he founded, the Educational Novelty Company, in Dayton, Ohio. Robertson’s toy patent cleverly incorporated his earlier calculating device to create an unusual hybrid, as he explains:
A number chart has never before been combined with any object resembling and representing a living creature which can be adjusted in relation to the chart to perform computations, thereby suggesting the idea of a calculating animal.Footnote 4
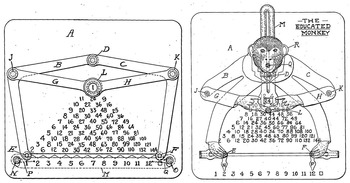
The US Patent Office issued the toy patent first, on 27 June 1916, followed by the calculating device patent on 26 November 1918 (Figure 11.2).Footnote 5
In addition to solutions to arithmetic problems, Consul offers a glimpse into twentieth-century views about education. Its invention coincides with the rise of public education and Progressivism in the United States.Footnote 6 Its use by one individual at a time fits the contemporary theories of learning as hands-on and child-directed, based on the philosophies of Johan Pestalozzi, Maria Montessori, and John Dewey.Footnote 7 As mathematical material culture, it includes the manually operated design of mechanical calculatorsFootnote 8 but with a consumer-friendly appearance. The monkey distracts from the complexity of the mechanical design and number charts that achieve the calculations, while bringing to mind the whimsy of performing animals. Consul embodies these cultural trends by providing fun ways to learn arithmetic and by bringing mathematics into the home as well as school.
Objects act as historical culture-carriers that offer unique insights into past lifestyles. Lorraine Daston asserts that ‘thinking with things is very different from thinking with words, for the relationship between sign and signified is never arbitrary – nor self-evident’.Footnote 9 Everything about objects is significant, but interpreting what exactly is ‘signified’ requires in-depth understanding of objects’ contexts. According to Samuel Alberti, objects must be placed in their world of people and ideas, as productions of a culture and not as isolated items.Footnote 10 With these approaches in mind, a calculating monkey becomes a guide to the mathematics, education, and playthings of a century-old culture. Unfortunately, a lack of recorded contemporary information, such as about how the object was designed, manufactured, and used, makes Consul’s physical construction and accompanying packaging the best available sources, as is often the case in object studies.Footnote 11
On the basis of the object itself, its printed instructions, and the two patents granted for its design, ‘“Consul”, the Educated Monkey’ is at once a calculating device, an educational aid, and a toy. How successfully did Consul fulfil these diverse purposes in the United States in the early twentieth century? I begin by exploring the object’s technical and mechanical meanings, then I analyse how it fits its context of educational theory and practice, and finally I consider its playfulness and cultural references, such as the evolutionary connotations of monkeys and the widespread popularity of vaudeville. This order matches Consul’s own development, on the basis of the chronology of its patents. It also matches typical object-study methodology, by first assessing the object as physical evidence and then investigating its more elusive cultural context. I suggest that Consul bridged the boundaries between school and home, work and play, and adulthood and childhood, making the red-suited calculating monkey a valuable informant about early-twentieth-century American culture.
Consul as Calculator
Consul is an efficient mechanical calculator. Its geometric design and clever mechanism suggest a creative and mathematically skilled inventor. After teaching high-school mathematics in Texas, Robertson moved to Dayton, Ohio, where by 1910 he was working as a draftsman and later as a designer for the National Cash Register Company.Footnote 12 He also founded the apparently short-lived Educational Novelty Company (1915–17).Footnote 13 Robertson designed his calculating device to make arithmetical number charts easier to use, as he explained in his 1918 patent: ‘To provide a quick and simple method of finding results on the chart by mechanical means thereby relieving the eye of having to follow columns and of making mistakes by locating results at the wrong intersections.’Footnote 14 The device makes arithmetic more accessible and reliable by simplifying chart-reading.
Both Robertson’s calculating device and toy patents contain terms and conventions from Euclidean geometry, reflecting his expertise as a maths teacher. Mathematical terms describe the object’s design: ‘The product of any two numbers of the series lies on an imaginary line which is the perpendicular bisector of another such line connecting the two numbers of the series.’Footnote 15 This sentence is found in both patents. Robertson uses more mathematical language in his calculating-device patent (perhaps because this patent and device are intended for a more mathematical audience), writing that the device’s ability to locate correct answers ‘can be proven by geometry’.Footnote 16
Robertson’s mathematical language is striking when compared with the descriptive language of a British patent for ‘a device or calculator for multiplying, dividing, adding and subtracting integers’ that is an exact replica of Consul, granted on 2 December 1918.Footnote 17 This patent, taken out by Charles Allaun of Leeds, uses inexact and non-technical language to describe ‘a jointed figure’ on the device, which in the diagrams is a monkey: ‘The legs of the figure are wide apart and disposed at an obtuse angle, the head is almost in a line with the body, the arms are bent at an angle and the forearms rest on the knees.’ A more detailed but not more mathematical description follows: ‘The above described jointed figure is mounted on the base plate a by means of studs q secured to the feet r of the figure and engaging with a slot s formed in the base plate.’Footnote 18 Allaun refers to diagram points with lower-case, italicised letters, unlike the upper-case letters used in geometric proofs and in Robertson’s patent. Neither does Allaun mention exact spatial dimensions or the geometric relationships of the device’s parts. These differences, and the apparent lack of connection between Allaun and Robertson, suggest that Allaun may have claimed a British patent by describing an American-manufactured Consul itself, as he didn’t copy the language or diagrams in Robertson’s patent. Thus, Robertson’s Euclidean language and mathematical descriptions, as well as his original invention of a number-chart-reading device, suggest that he was first a mathematical inventor and later applied these skills to the toy industry, especially since he applied for the calculating-device patent before the toy patent (though the toy patent was granted first).
Detailed instructions on how to multiply, divide, factor, add, and subtract using Consul present it as a do-it-all calculating machine. Conducting these operations using Consul is ostensibly so easy that a child can do it (though Consul’s fragility makes this rather unrealistic). Mass manufacture of its simple design and small size would have been cheap and efficient, making Consul accessible to adults who wanted to simplify their use of arithmetic number charts without investing in a newfangled expensive calculating machine.Footnote 19 Thus, Consul offered an easier version of number charts and a cheaper, though perhaps less dignified, alternative to mechanical calculating machines designed for adults.
Consul as Teacher
Although Robertson’s second patent is for a ‘toy’, he specifies that ‘my invention relates to toys for educational purposes.’Footnote 20 Specifically, this invention ‘is intended to interest the child and increase his knowledge of numbers and number tables’.Footnote 21 Irrespective of whether educational toys were playthings that claimed to teach or learning tools that imitated playthings, there was a growing market for them in early-twentieth-century United States. This market is evident in the name of the company that manufactured most of the surviving Consuls: The Educational Toy Manufacturing Co. of Springfield, Massachusetts. Robertson’s company, the Educational Novelty Company of Dayton, Ohio, is the assignee of the two patents. But was Consul a good ‘educational’ object according to philosophies of learning at the time?
Consul meets the contemporary demand for manipulative, hands-on objects as physical representations of knowledge that children could interact with directly. The importance of learning through experience, inquiry, and physical objects was stressed by education scholars such as J. H. Pestalozzi in early-nineteenth-century Switzerland, Maria Montessori in early-twentieth-century Italy, and John Dewey in the late-nineteenth- and early-twentieth-century United States. Visual and physical ways of learning arithmetic grew in popularity, exemplified by abacuses in nineteenth-century classrooms. In the late nineteenth century, ‘tools for group demonstration such as the teaching abacus gave way to devices for a single child.’Footnote 22 By 1900, ‘the material used in the schoolroom as objective aids is limited and highly artificial, consisting of tiles, pegs, splints, toothpicks, squares of cardboard, etc.’Footnote 23 These simple objects served as counters to help children learn the physical meaning of arithmetic.Footnote 24
Consul matches this trend of single-user educational tools, but it does not serve the accompanying educational philosophy. Pestalozzi, Montessori, and Dewey called for hands-on activities to encourage children to ask their own questions and explore their world directly.Footnote 25 Likewise, and in contrast to the previous pedagogy of memorisation and recitation, educator David Smith argued in his 1913 book The Teaching of Arithmetic that mathematics learning should be more active for students:
There has for a century been a tendency away from what is called the direct method of imparting number facts, and toward the rational method. This means that instead of stating to a class that 4 + 5 = 9, and drilling upon this and similar relations, the schools have generally tended to have the pupils discover the fact and then memorize it. The experience of a century shows that this tendency is a healthy one.Footnote 26
Smith believes this ‘rational’ method is successful because it gives a student the freedom to think: ‘A child likes to be a discoverer, to find out for himself how to add and multiply, always under the skillful guidance of the teacher.’Footnote 27 Educational mathematics objects were tools, not answer-givers. Counters had to be counted accurately, and rulers and protractors only provided measurements to serve as the basis of a student’s further calculations, such as of area and volume. A child must understand how these tools work and how to interpret the information they yield to reach a correct answer.
Consul’s packaging personifies an ideal teacher because ‘it makes no difference to the monkey whether children are bright or stupid. He never loses patience at having to answer their questions,’ suggesting that children ‘discover’ and learn from Consul by asking ‘him’ questions. But Consul does not allow such ‘discovery’ of arithmetical principles because it can answer only a very limited type of question, not the open-ended investigative questions that twentieth-century educators believed led to true learning. Specifically, after the user has pointed the monkey’s feet at appropriate numbers, the answer appears without further user input or thought-processing. Consul thus yields answers regardless of the user’s knowledge of mathematics. The user must only arrange the monkey correctly: ‘To multiply, adjust each of the monkey’s feet to point directly at a number. The monkey’s fingers will then locate the product of the two numbers.’ These directions imply that the monkey itself carries out the calculation. Similarly, to subtract the user must move one monkey foot and one monkey hand to the numbers in question, and then ‘the other foot will be found pointing at the difference.’ The answer is literally pointed to, and a child learning arithmetic would have no idea how that answer was reached. Robertson even writes in his 1916 patent that ‘the idea of a calculating animal’ would hold a child’s attention; he does not mention Consul’s innovative mathematical design as appealing for young users.Footnote 28
Nevertheless, the packaging presents Consul as teacher as well as calculator: ‘It teaches the complete multiplication table. It teaches the complete addition table. It can add, subtract, multiply, divide, or factor elementary numbers.’ The abilities to teach and to do arithmetic are merged, suggesting an underlying pedagogy in which giving answers to arithmetic problems is the same as teaching arithmetic. Thus, it seems the device could not help children understand arithmetic facts or learn mathematics according to contemporary pedagogy, but could only provide correct answers – the opposite of Smith’s ‘rational method’.
However, the magic or perhaps the ‘education’ behind Consul’s ability to calculate is revealed in an included ‘mathematical puzzle which has advanced students guessing’ (Figure 11.3). This puzzle presents Consul’s construction as a geometric diagram of Consul’s joints with information about angle congruence and segment length, whose relationships a student must prove. Although the answer is not provided, phrasing Consul’s construction as a geometry problem reveals the object’s seemingly mysterious calculating ability as merely an application of familiar mathematics, at least for advanced students. I have found no records of early-twentieth-century users’ impressions of Consul; however, twenty-first-century mathematics teachers recommend that high-school students build their own Consuls with paper and metal fasteners.Footnote 29 This hands-on activity requires students to apply geometry and algebra as well as arithmetic. As an embodied geometric proof, Consul also appeals to today’s hobbyist model-builders, who replicate the device using various media.Footnote 30 It is possible that teachers taught the same activity a century ago. Consul thus can serve as a geometric proof as well as a calculator, though the device’s workings were most likely to have been a black box to young users.
Calling the geometric proof a ‘puzzle’ presents it as fun, an important component of learning according to Pestalozzi, Montessori, Dewey, and Smith. Pestalozzi advocated mathematics lessons even for young children, challenging the norm of introducing arithmetic only at age twelve. According to Smith, Pestalozzi ‘concealed the drill under the guise of play, but play with a definite purpose’ so as to interest young children.Footnote 31 Montessori designed ‘materials’ to guide children to understand arithmetic, such as labelled boards on which to arrange beads, which children found so engaging that they begged to take them home. One youngster reportedly threatened that, ‘“Unless she gives us the material for the multiplication table we won’t come to school any more.”’ Montessori took this demand as a sign of success: ‘The multiplication table, the bug-bear of all children, had become so attractive and tempting a thing that it had made wolves out of my lambs!’Footnote 32 The right materials thus had the power to make dreaded topics enjoyable, even if children acted rudely in their efforts to access them. Smith also valued students’ enjoyment. He filled twenty pages of his book with ‘number games for children’, including competitions and interesting ‘tricks’ about arithmetic to stimulate students’ interest in mathematics.Footnote 33
The inclusion of ‘an entertaining and instructive game for children’ in Consul’s packaging matches this trend.Footnote 34 This game, called Multe, an acronym for ‘Many Useful Lessons Taught Enjoyably’ and perhaps also short for ‘multiplication’, involves children competing for accuracy in arithmetic facts. After all of the players have completed ten facts, ‘each player who is in doubt as to whether the answer is correct is allowed to consult his monkey’ (with ‘consult’ perhaps being a play on Consul’s name). Consul is the answer-checker. The instructions seem to expect that Multe will be played in a classroom. These directions reflect the Progressive ideology of education as social reform, and thus teachers as valuable reformers:Footnote 35 ‘The mechanism of the Educated Monkey device … offers teachers an opportunity to develop a fine art in teaching children numerical tables and stimulating even the dullest to their best.’ Defining teaching as ‘stimulating’ children portrays teachers as the driving force behind effective educational use of Consul, in line with Pestalozzi’s, Montessori’s, Dewey’s, and Smith’s argument that teachers should lead students towards understanding through activities rather than memorising facts.
Multe is intended to make mathematics fun and engaging, the game’s instructions claiming it ‘can be used to turn certain kinds of work into play’. Like many arithmetic games, including some described by Smith, Multe uses competition to motivate children to memorise arithmetic facts. Thus, it more closely resembles an interactive form of mathematical drill than the child-directed, exploratory learning that early-twentieth-century educators recommended. I have found no evidence of Consuls being purchased or used by school classrooms, so it’s possible that Multe was written only in the hope of appealing to the large economic market of school supplies. Furthermore, the presentation of Consul as a plaything suggests that its main target audience was parents, not schools.
Consul as Toy
Consul is a self-professed ‘classic in the toy line’, as printed on its paper folder packaging, and its charming clothes-wearing monkey and bright colours are assumedly meant to appeal to children. But, upon closer examination, Consul is a poorly designed toy. The thin, lightweight backplate and monkey figure would be damaged by clumsy handling, and the monkey’s joints are fragile and could easily be knocked out of alignment, which would ruin the device’s calculating ability. Consul may seem fragile today because the surviving examples are up to a century old. However, a warning on the packaging suggests that Consul’s finicky operation is original: ‘If the feet stick at any position, do not force their movement but loosen by moving the arms.’ Consul’s small size suggests intended use by small hands, but I suspect most school-age children lack the dexterity and patience necessary to work its calculating function.
Furthermore, Consul’s use is not intuitive, and the included instructions are not child-friendly. The instructions printed on the object itself (in its post-1916 versions) are brief: ‘Set feet to point at two numbers/Fingers will locate their product.’ The instructions on the packaging are small, dense text. More instructions are printed on the back of the enclosed addition number-chart, which explain how to divide, factor, add, and subtract using Consul (Figure 11.3). But these are also in small print and use technical terms that were probably alien to children learning basic arithmetic. For example, ‘To subtract: Adjust the monkey so that one foot points at the subtrahend and the fingers point at the minuend. The other foot will be found pointing at the difference.’ To understand these directions, a child must be a good reader, familiar with mathematical terms, and patient enough to locate the small-printed words in an obscure location on the packaging.
Consul’s metal construction resembles contemporary mechanical toys like train models and building sets, such as the popular 1914 Tinkertoys. Animal toys were also common, such as the posable figurines in the Humpty Dumpty Circus of 1910 and the teddy bear craze of 1906.Footnote 36 This educated monkey, however, is not cute. It is a garishly awkward creature. Who then is the intended audience for Consul?
One selling point may be that its name and appearance, from red-polka-dot bowtie to comb tracks on its furry pate, differentiate it from just any monkey. These details specifically link the object with a trained chimpanzee called Consul that hit the New York vaudeville stage in 1909, six years before Robertson’s patent applications.Footnote 37 A star like Consul would have been well known, as vaudeville was a popular and reputable form of entertainment among people of all ages and social classes from the 1890s to the 1920s in the United States. Vaudeville defined itself as more moral than ‘common entertainments of the concert saloons, the dime museums, and the circus’. ‘Polite vaudeville’ in particular promised ‘to provide a respectable place and decent entertainment that families could patronize without damage to their reputations’.Footnote 38 Animal acts were considered respectable and moral, and they especially appealed to children, perhaps drawing on the prominence of anthropomorphised animals in children’s literature since the middle of the eighteenth century.Footnote 39 Polite vaudeville’s popularity meant that animal stars were widely recognisable to children and adults.
Consul’s arrival in New York from Europe was big news. News articles claimed that this ‘educated monkey’ had human abilities – he wore clothes, played shuffleboard, and lit and smoked cigarettes. He could also talk: ‘Drowski [Consul’s manager] spoke to Consul in French, and the chimpanzee responded with gutteral [sic] sounds that seemed to be understood by his manager.’Footnote 40 In June 1909, a New York Times article documented this priceless exchange: ‘To the next [reporter’s] question, “Do you like wearing clothes?” the chimpanzee replied, “garrrrr-egre-grummm-goora-umn.” This was translated by Drowski to mean: “Have any of you got a cigarette, I want to smoke.”’ These decidedly un-monkey-like behaviours made Consul a big hit, and, according to Robertson’s device, ‘educated’.
What then did it mean for a monkey to be educated? According to psychologists and popular culture, it meant being able to behave like a human. In 1909, Pennsylvania psychologist Dr Lightner Witmer used intelligence tests designed for ‘backward’ children to test a performing chimpanzee named Peter, ‘who has been appearing in vaudeville throughout the country as an example of “a monkey with a mind”.’ In a 1909 New York Times article, Witmer concluded that ‘the chimpanzee is educated in a real sense and that he has the power of reasoning … Peter, under the proper conditions, might be taught to read, write, and speak.’Footnote 41 Psychologist William Hornaday, who also studied trained chimpanzees, was not surprised by Witmer’s findings. He described the trend of performing monkeys: ‘In 1904 the American public saw Esau. Next came Consul, – in about three or four separate editions! In 1909 we had Peter.’Footnote 42
There seem to have been many Consuls, or perhaps, thanks to these vaudeville stars, ‘consul’ became a generic word for a trained monkey or a chimpanzee. This usage even crossed into scientific terminology when, in 1933, the paleontologist Arthur Hopwood named a new genus of ancient primate Proconsul, meaning ‘before chimpanzee’.Footnote 43 This generalisation of the name may also explain the caption of a 1909 photograph of a suit-wearing, cigar-smoking chimpanzee aboard a transatlantic ship: ‘“Consul Peter” – smoking’ (Figure 11.4). Is this smoker Consul or Peter? According to Hornaday’s chronology of trained chimps in America, it could be either. Or perhaps the author intended ‘consul’ to mean ‘primate’ or perhaps even ‘educated monkey’, followed by an individual’s name, Peter. There is similar confusion about a 1909 film made about Consul’s arrival in the United States (Charles Urban’s Consul Crosses the Atlantic), in that sources disagree whether Consul or Peter was its simian star.Footnote 44 Others explain that the movie was about the famous Consul, whose behaviour was then imitated by ‘Peter the Great’ and other celebrity chimpanzees.Footnote 45 Whichever particular primate Robertson’s device was named after, ‘consul’ was a well-known word associated with humanlike monkeys in the early twentieth century.

These chimpanzees are documented onstage as dressing like humans, eating with table manners, smoking, dancing, riding bicycles, and roller-skating, but no mention is made of any Consuls doing mathematics.Footnote 46 Thus, the real Consuls did quite different things from Robertson’s calculating Consul. Does this imply that arithmetic is so easy that even monkeys can do it? Or, on the other hand, is it more impressive for a monkey to do maths, as a uniquely human ability? The latter makes sense in the light of late-nineteenth-century psychologists’ supposedly successful attempts to teach monkeys to count and then perform their ‘simian arithmetic’ for interested colleagues and journalists as evidence of intelligence.Footnote 47 But language was the telltale marker of humanlike animals, not mathematics.
The aesthetics of Consul the calculator speak more to performance than to intelligence. For example, its backplate is muted yellow with an ornately patterned dark green trim (marked with tiny plus signs), suggesting the sepia tones of early photographs and cinema, and the monkey’s bright red suit invokes the spectacle of vaudeville. There are no scholarly symbols on the object or instructions, such as books, mathematical instruments, or eyeglasses to represent Consul’s ‘educated’ status. Consul looks more like an entertainer than a mathematician.
The idea of a monkey doing mathematics may have appealed to children for its novelty, but the underlying theme of a humanlike monkey would have been more meaningful to the Darwin-aware adult population. Evolutionists and anti-evolutionists alike believed that children and primates shared many developmental and psychological characteristics, such as cuteness, mischief (especially a love of stealing), and emotional expression.Footnote 48 Hornaday described the appeal in 1922: ‘During the past twenty years, millions of thinking people have been startled, and not a few shocked, by the amazing and uncanny human-likeness of the performances of trained chimpanzees on the theatrical stage.’Footnote 49 As Constance Clark wrote in God – or Gorilla: Images of Evolution in the Jazz Age, ‘monkeys were everywhere in the 1920s.’Footnote 50 Although Clark does not mention primate performers or toys in her book, the association between monkeys and evolution was so ubiquitous that the highly publicised trial of 1925 concerning the teaching of evolution in public schools was called the Scopes ‘monkey’ trial.Footnote 51 Both the performing and the calculating Consuls drew on the public fascination with monkeys as symbols of evolution and human development.
Robertson’s 1916 patent diagram is labelled ‘The Educated Monkey’, not ‘Consul’. Perhaps ‘Consul’ was added later for its attractive vaudeville association. But the famous Consuls appeared before 1909, and Peter died in 1910.Footnote 52 Hornaday mentioned no famous chimps after Peter. Robertson’s calculating toy was probably first produced around 1915, when he applied for the two patents.Footnote 53 Would a vaudeville star, even one as famous as the Consuls and Peter, still be recognised by children at least five years later? Both childhood and stardom are short-lived. But it is likely that adults would still remember the famous chimps of the 1900s in 1915, even if children did not. Designing toys that appealed to parents more than children was common before the 1930s, when companies began to target children as consumers in their own right.Footnote 54 This focus on adults is also acknowledged on the packaging, which describes Consul as ‘a device which interests both young and old’. Furthermore, the Educational Toy Company of Springfield, Massachusetts, advertised Consul in 1920 in Illustrated World, a magazine for adult science and technology enthusiasts. The advertisement does not market Consul as a fun novelty or as a calculator for adults, but as an educational device: ‘“CONSUL”, THE EDUCATED MONKEY should be in every home, for he points out The Royal Road to the Multiplication Table … He Makes Arithmetic Fun.’Footnote 55 This angle matches the company’s speciality in making education fun, as shown by its name. The advertisement’s placement on a page of ads for other gadgets, including a telescope and a newfangled kerosene burner for stoves, targets parents rather than kids. The advertisement invites consumers to send the company 35 centsFootnote 56 for an educated monkey, ‘or a dollar for three’; an order of only one or three monkeys seems more appropriate for families than schools. Consul’s marketing seems to appeal to a dual audience of school-age children and their parents, thanks to the adults’ nostalgia for vaudeville as well as their aspiration for their children to learn mathematics.
Conclusion
Finding a vaudeville celebrity remade as a mechanical calculator may seem surprising. This uniquely twentieth-century cultural meaning gives this charming metal device an air of sophistication, fame, and fun. The object invites children to practice their sums with not just any suit-wearing monkey bent into acrobatic poses, but with an individual suit-wearing monkey. The star of Consul Crosses the Atlantic can participate in something as seemingly mundane as multiplication, thereby lending mathematics an exalted status.
The calculating monkey dissolves some of the boundaries we imagine about historic lifestyles, such as between school and home and between adulthood and childhood. For example, children can now ‘perform’ calculations, at home or at school, as mathematical drill disguised in objects, games, and subtle hints of vaudeville. Consul brought aspects of school, such as arithmetic facts, to children’s homes in the form of an educational toy. Likewise, it may have brought aspects of home, such as fun and games, to school, if Multe’s instructions for classroom play were actually followed. Also, this supposed toy was not marketed in ways that would capture children’s attention. It is not a cute, sturdy object like the other animal figurines in a child’s toy box at the time. Its name probably meant little to children of the late 1910s and early 1920s, though their parents would have well remembered the individual performing chimps of the first decade of the twentieth century. Thus, this object uses nostalgia for past celebrities plus future hopes for children to learn mathematics to convince adults to purchase this mechanical calculator.
The combination of a calculator, teacher, and toy in one object presents mathematics as important in early-twentieth-century American society. Mathematics was considered an avenue to individual learning and social progress, hence the rise of toys that were claimed to help children learn arithmetic. Robertson’s device perhaps functions best as a calculator, with marketing and decoration that reflect contemporary trends in education and popular culture. His sequence of patents supports this interpretation, as his geometry-based mechanical calculator later acquired aspects of education and play. Robertson added a toy-like representation of a monkey, and later the name of a cultural icon, to make his ‘calculating animal’, and the object was packaged in the language of education. The connection between these issues, as well as the social value placed on educational toys and on learning as an experiential process, reveals the intricate ways in which we create physical forms to meet social functions. Historians then reap the benefits, and face the challenges, of interpreting these forms as rich evidence of the culture they represent.